Связанные контуры как полосовой фильтр

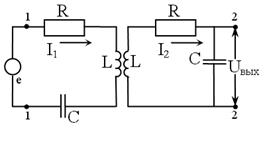Идеальный фильтр должен иметь П-образную частотную характеристику и линейную фазовую характеристику в полосе пропускания. Для решения многих радиотехнических задач необходимы фильтры, частотная характеристика которых приближается к идеальной. Для создания таких фильтров используется система контуров, связанных между собой или общим магнитным полем (индуктивная связь), или общим электрическим полем (ёмкостная связь).

Рассмотрим два одинаковых контура (R₁=R₂=R, L₁=L₂=L, C₁=C₂=C) с индуктивной связью (рис. 1).

Коэффициент передачи такой схемы:

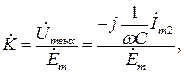(1)

где 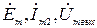- комплексные амплитуды э.д.с., силы тока во втором контуре и напряжения на конденсаторе.

Для нахождения амплитуды силы тока в контурах запишем систему уравнений Кирхгофа:

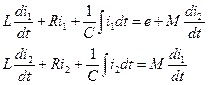(2)

М – коэффициент взаимной индукции.

Воспользовавшись методом комплексных амплитуд, запишем в комплексной форме: 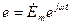, , 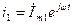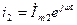. Подставив эти значения в систему (2) получим систему уравнений:

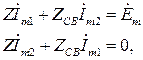(3)

где 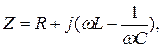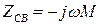- сопротивления связи.

Решая систему уравнений (3), находим

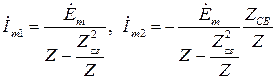(4)

Из первого соотношения (4) можно заключить, что связь первого контура со вторым контуром в электрическом отношении эквивалентна включению в первый контур дополнительно вносимого сопротивления Z_вн:

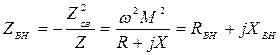, (5)

где: .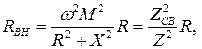

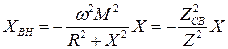С энергетической точки зрения наличие 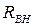объясняется тем, что часть энергии источника поступает во второй контур и поглощается в его активном сопротивлении. Наличие 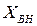связано с тем, что ток I₂ наводит э.д.с. взаимной индукции в первом контуре. Таким образом, влияние второго контура на первый приводит к увеличению эквивалентного активного сопротивления первого контура на 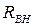и изменению его эквивалентного реактивного сопротивления на 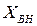. Следовательно, эквивалентное сопротивление симметричной системы двух связанных контуров, измеренное на входных зажимах «11» можно представить в виде: 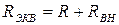, 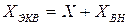. На собственной частоте :

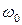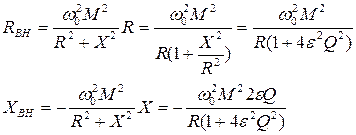(6)

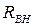и 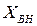зависят от частоты сигнала (от расстройки 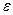). При 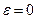, , 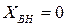а 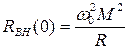, имеет максимальное значение. В зависимости от М 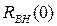может быть как больше, так и меньше собственного активного сопротивления R первого контура.

Если 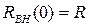, связь называется критической.

Если 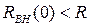, связь слабая.

Если 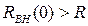, связь больше критической.

При критической связи .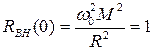

Умножив числитель и знаменатель левой части на L², получим:

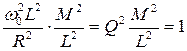
Количественно связь между контурами характеризуется коэффициентом связи 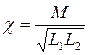. При одинаковых контурах L₁=L₂=L, 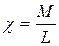определяет, какая доля собственного магнитного потока катушки первого контура проходит через катушку второго. При критической связи .

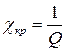Найдём резонансные частоты системы из условия равенства нулю её реактивного сопротивления .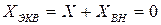

В последнее уравнение подставим (6), учтём, что 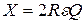, а 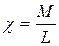, получим:

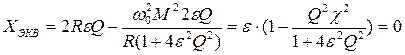(7)

Получили уравнение (7) третьей степени относительно 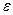. Корни этого уравнения

.

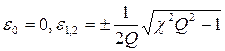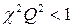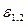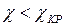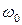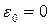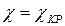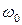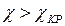При связи меньше критической ( ) корни мнимые и не имеют физического смысла. Следовательно, при система имеет одну резонансную частоту , определяемую действительным корнем ( ). При все три корня равны 0, система в этом случае имеет одну резонансную частоту . При все три корня уравнения (7) действительны и, значит, система имеет три резонансных частоты, одна из которых 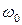, а две другие

.

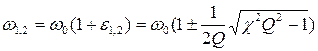Частоты 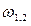называют частотами связи, или нормальными частотами системы.

Для связанных контуров при 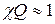можно получить фильтр с более широкой полосой пропускания по сравнению с одиночным контуром и амплитудно-частотную характеристику, близкую к идеальной П-образной.

Определим значение коэффициента передачи. Для этого подставим I_m2 из (4) в (1), получим:

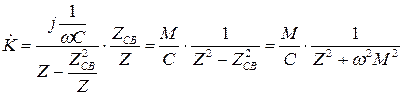(8)

Преобразуем знаменатель (8), учитывая, что расстройка 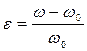и 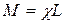, тогда:

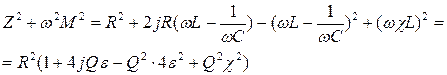
Подставим последнее выражение в (8):

.

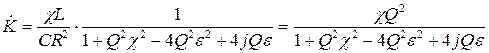Откуда

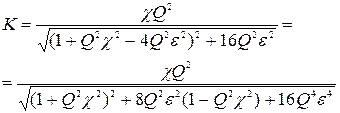(9)

На рис. 24 приведено семейство зависимостей K( 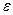), описываемых уравнением (9) для различных значений .

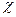При .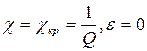

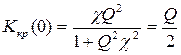Ширина полосы пропускания связанных контуров определяется также, как и для одиночного:

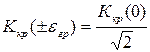или .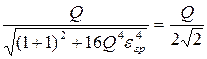

Отсюда 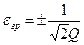. Тогда относительная полоса пропускания при критической связи (кривая 2, рис. 24) 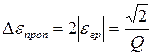в 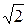раз больше, чем у одиночного контура.

При 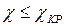амплитудно-частотная характеристика не имеет провала при 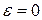(кривая 1, рис. 24). При слабой связи ( )

.

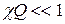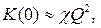
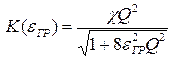Отсюда .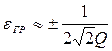

Таким образом, при слабой связи полоса пропускания связанных контуров уже, чем у одиночного контура.

При 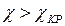амплитудно-частотная характеристика становится двугорбой, с провалом при 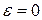(кривая 3, рис. 24). Оптимальным считается такое значение 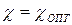, при котором коэффициент передачи в минимуме К(0) в 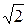раза меньше, чем в максимуме K_max.

В этом случае можно составить два уравнения:

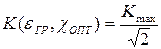(10а)

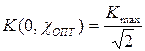(10б)

Учитывая, что при 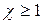модуль коэффициента передачи К на частотах связи 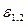не зависит от 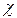и равен модулю коэффициента передачи при критической связи и 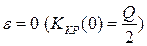, получим:

.

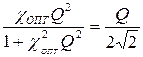Откуда

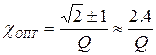(11)

Подставим (11) в (9), и учитывая (10а), получим:

.

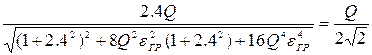Отсюда

.

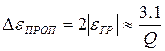Следовательно, в оптимальном случае 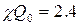, а полоса пропускания фильтра связанных контуров примерно втрое шире, чем у одиночного контура-фильтра.

Глава 5.

Электронные приборы.