Метод узловых потенциалов (МУП).

Содержание задания

· Для полученной схемы рассчитать все токи методом контурных токов.

· Проверить расчет по второму закону Кирхгофа и по уравнению баланса мощностей.

· Рассчитать ток в ветви №2 по методу узловых потенциалов, приняв равным нулю потенциал узла, указанного в задании.

· Рассчитать ток в ветви с сопротивлением R₄ методом эквивалентного генератора, рассматривая схему относительно указанной ветви как активный двухполюсник.

Заданные параметры:

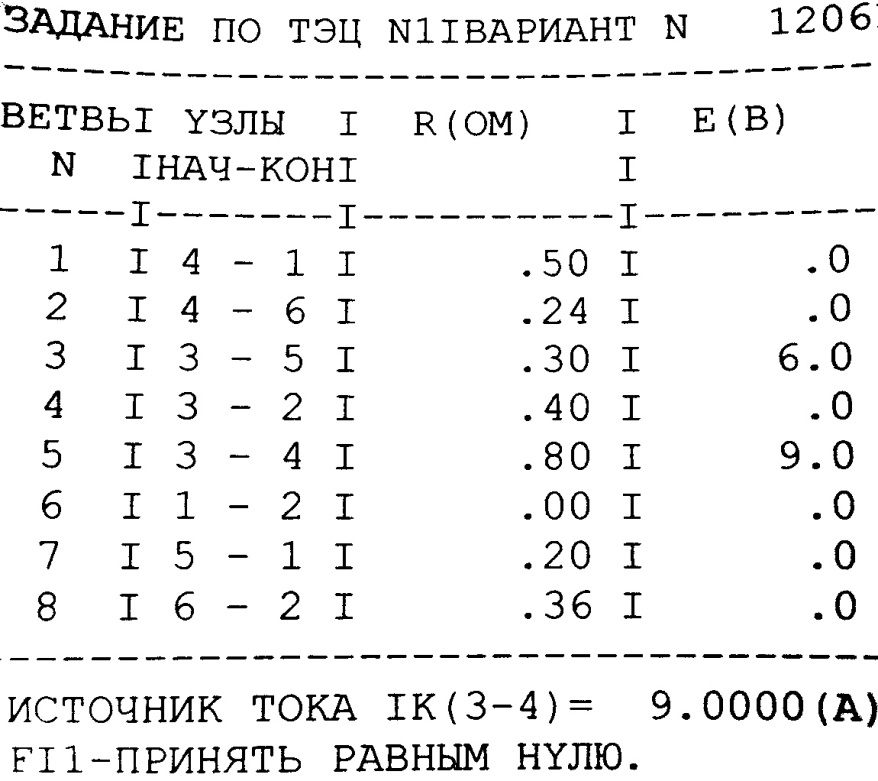
Метод расчета

Расчетные величины

1. Метод контурных токов

I1, А

I2, А

I3, А

I4, А

I5, А

I6, А

I7, А

I8, А

5.70

4.75

2.02

-12.47

1.45

7.72

º I3

º I2

2. Баланс мощностей.

Pпотр, Вт

Pген, Вт

95.74

95.74

3. Метод узловых потенциалов

j1, В

j2, В

j3, В

j4, В

I2, А

º j1

-4.99

2.85

4.75

4. Метод эквивалентного генератора.

EЭ = U23ХХ, В

RЭ = R23, Ом

I4, А

9.24

0.34

-12.47

Исходная схема.

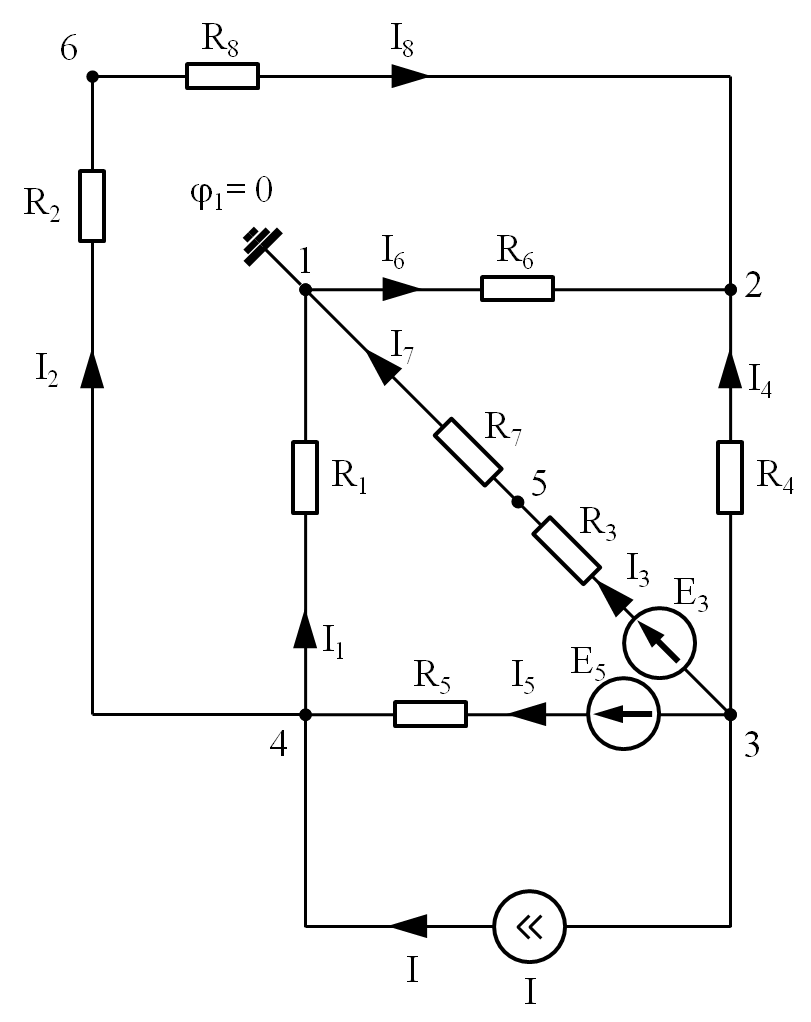
По условию задания R₆= 0. Тогда схема упрощается:

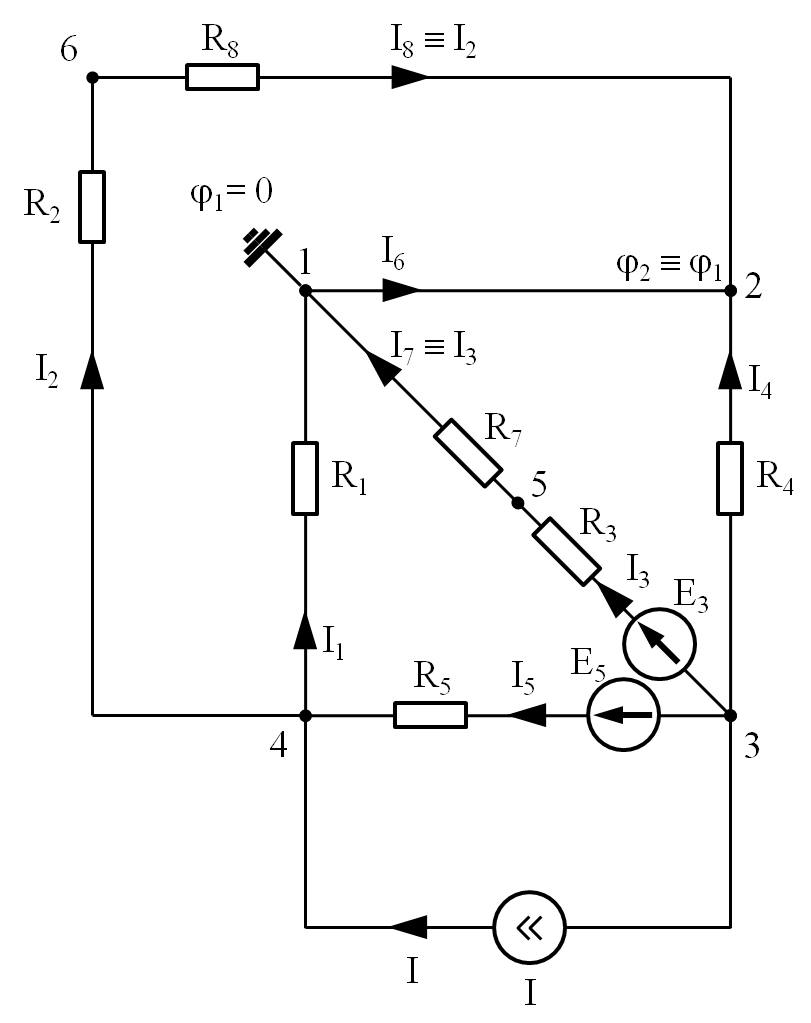
Сразу отметим, что, т.к. узлы 1 и 2 схемы соединены ветвью с нулевым сопротивлением, то их потенциалы одинаковы (но ток I₆ может быть не равен 0).

Кроме того, очевидно, что ветви 2 и 8 представляют собой, фактически, одну ветвь, т.к. в своей общей точке 6 они соединены без ответвлений и, следовательно, I₈ º I₂.

Ветви 3 и 7 также представляют собой, фактически, одну ветвь, т.к. в своей общей точке 5 они соединены без ответвлений и, следовательно, I₇ º I₃.

Метод контурных токов (МКТ).

В схеме 7 независимых ветвей (с одним и тем же током, без ответвлений) и 4 узла, в которых соединяются более, чем 2 ветви (т.е. 3 и больше). Для расчета по методу контурных токов нужно N_К независимых контуров.

N_К = m - (n - 1), где m = 7 - число независимых ветвей,

n = 4 - число узлов, в которых соединяются более, чем

2 ветви.

Т.е. в нашем случае N_К = 4. Выбранные независимые контуры и направления контурных токов показаны на рисунке.

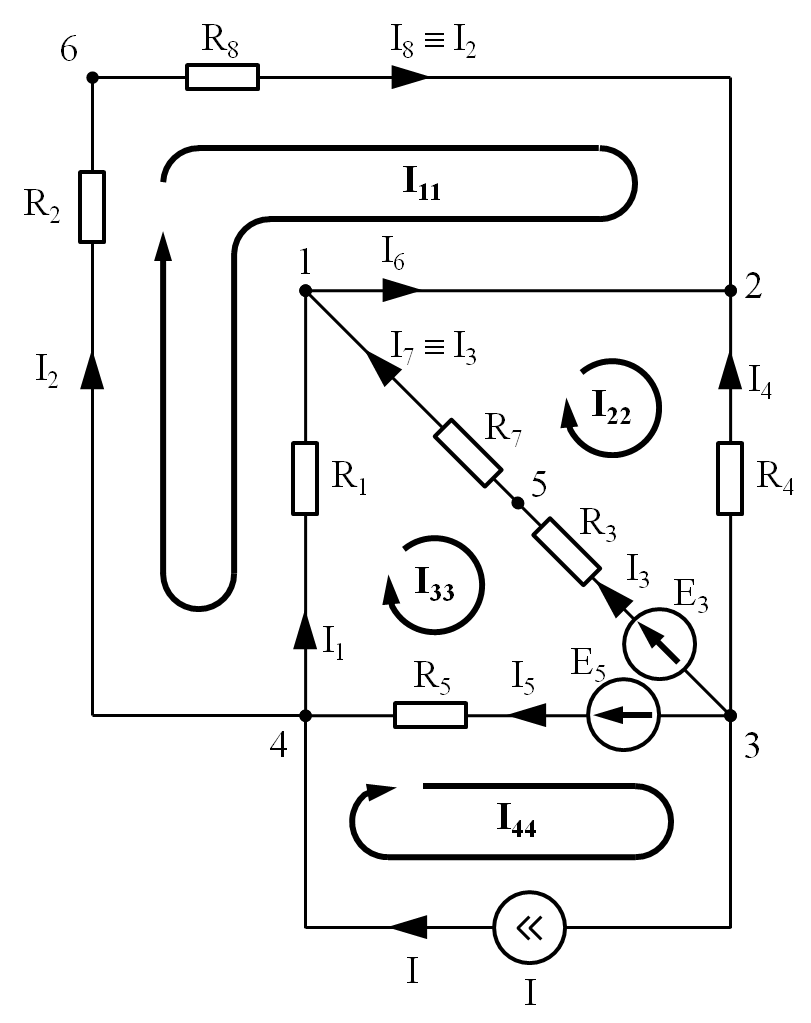
По ветви с источником тока протекает один контурный ток I₄₄, совпадающий по направлению с током источника. Следовательно,

I₄₄ = I = 9 А

Т.е. необходимость рассмотрения контура 44 отпадает.

Уравнения по второму закону Кирхгофа для остальных контуров (11, 22 и 33) при их обходе в направлении протекания контурных токов принимают вид:

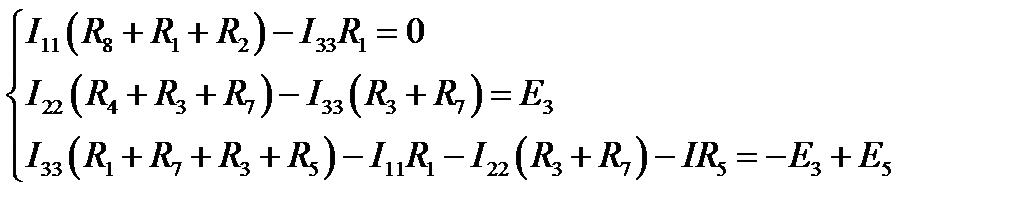
Перепишем полученную систему уравнений в более удобном для решения виде:

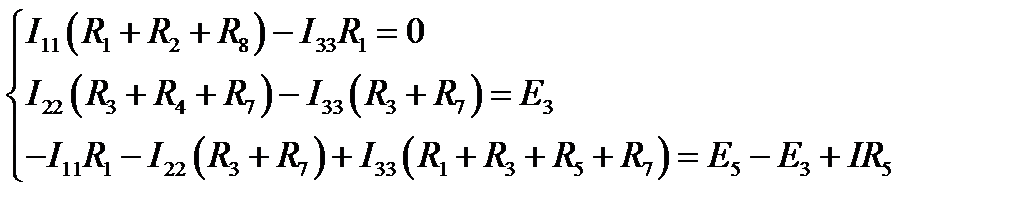
В матричной форме: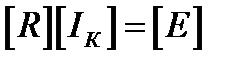

где

, ,

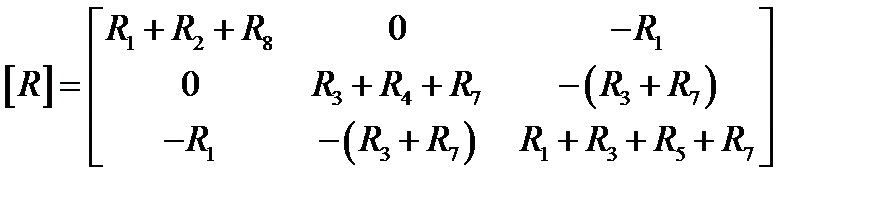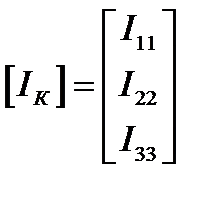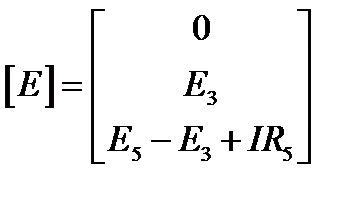
Решение можно найти, вычислив матрицу, обратной матрице [R]:

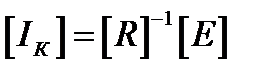
В нашем случае

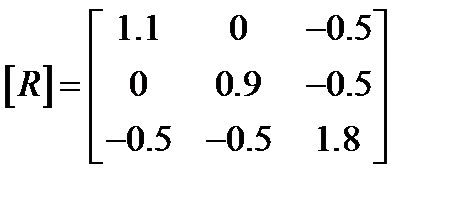
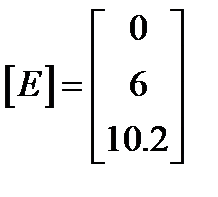Þ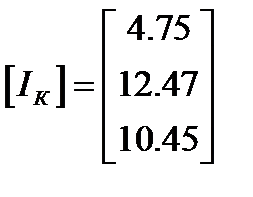

Т.е. контурные токи равны

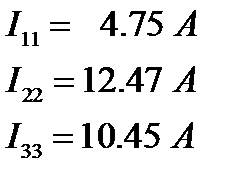
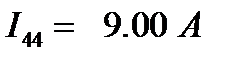
(как уже отмечалось ранее, этот контурный ток равен току источника тока)

Найдем реальные токи в ветвях. Для этого алгебраически просуммируем соответствующие контурные токи (контурные токи, совпадающие по направлению с выбранным направлением реального тока, учитываем с плюсом, в противном случае - с минусом).

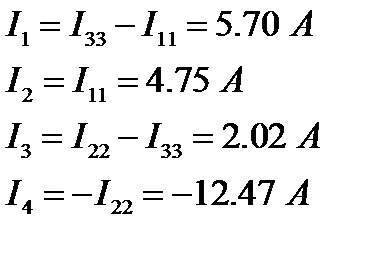
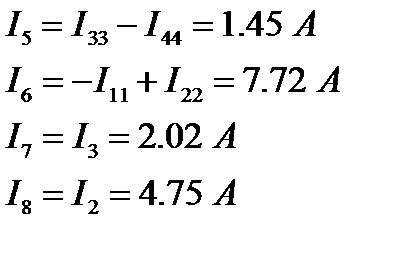
Проверка решения.

1-й закон Кирхгофа для узлов выполняется автоматически, это следует из алгоритма нахождения реальных токов через контурные.

2-й закон Кирхгофа для контуров.

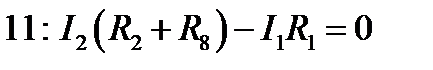
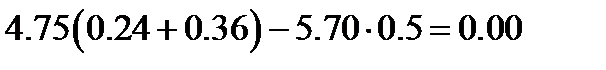
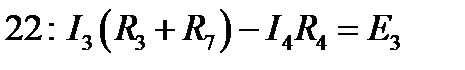
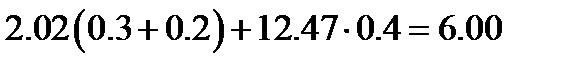
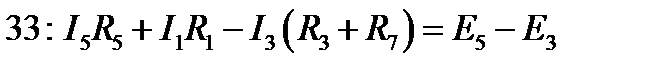
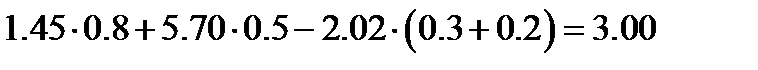
Вывод: найденные токи удовлетворяют законам Кирхгофа.

Баланс мощностей.

Уравнение баланса мощностей имеет вид

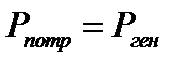
Источник ЭДС работает в генераторном режиме, если ток в источнике одного направления с ЭДС. Для такого источника P_ген = E × I > 0. В противном случае источник ЭДC потребляет энергию и P_ген = E × I < 0.

Источник тока работает в генераторном режиме, если напряжение на его зажимах направлено навстречу току источника. Для такого источника P_ген = U × I > 0. В противном случае источник тока потребляет энергию и P_ген = U × I < 0. В нашем случае напряжение на зажимах источника тока есть U₄₃ = E₅ - I₅ R₅

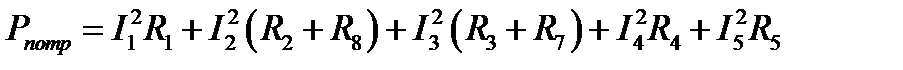
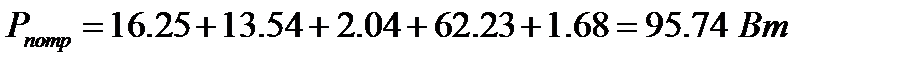
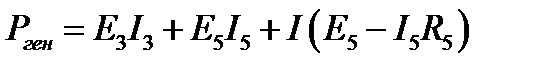
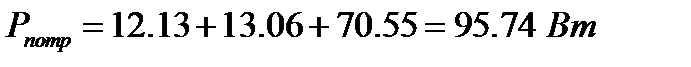
Вывод: найденные токи удовлетворяют уравнению баланса мощностей.

Метод узловых потенциалов (МУП).

Требуется рассчитать ток в ветви №2 по методу узловых потенциалов, приняв равным нулю потенциал узла №1. В общем случае для расчета по МУП нужно N_У узлов:

N_У = n - 1, где n - число узлов, в которых соединяются более, чем 2 ветви.

Еще раз отметим, что в нашей схеме есть 4 узла, в которых соединяются более, чем 2 ветви. Это узлы №1, 2, 3 и 4. Т.е. в нашем случае N_У = 3. Причем потенциалы двух узлов одинаковы и в соответствии с заданием j₂ = j₁ = 0. Поэтому достаточно составить уравнения только для узлов 3 и 4.

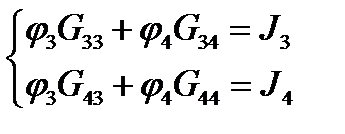
где

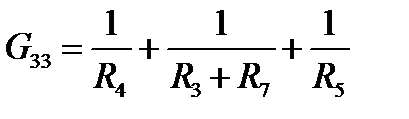- сумма проводимостей ветвей, сходящихся в узле 3,

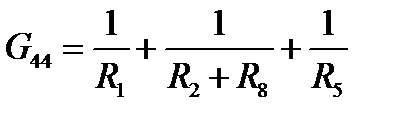- сумма проводимостей ветвей, сходящихся в узле 4,

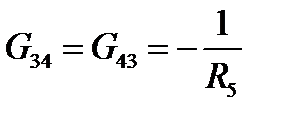- взятая со знаком минус сумма проводимостей ветвей, непосредственно соединяющих узлы 3 и 4,

J₃ и J₄ - узловые токи, в нашем случае они равны

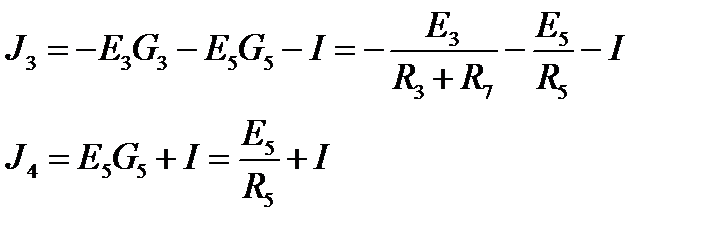
(в формировании узлового тока участвуют ветви, подходящие к узлу и содержащие источники ЭДС и/или тока; вклад ЭДС ветви в формирование узлового тока равен ±E × G, где G - проводимость ветви, причем если ЭДС направлена к узлу, то используем знак "+", а если от узла, то знак "-"; если ток источника тока "втекает" в узел, то он берется со знаком "+", а если "вытекает" из узла, то со знаком "-").

Система из 2-х линейных уравнений легко решается:

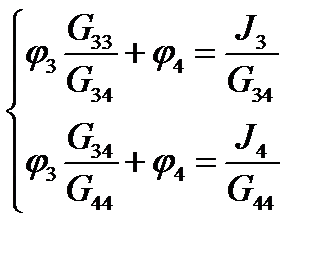
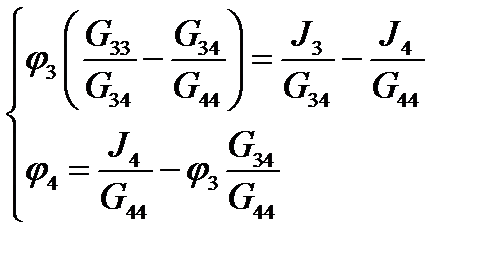
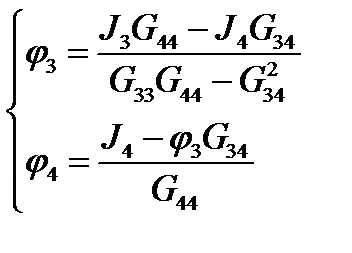
В нашем случае

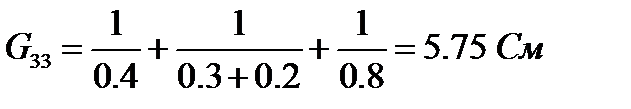
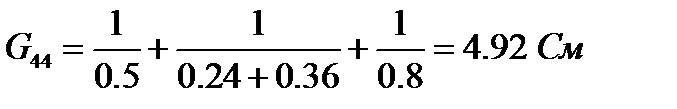
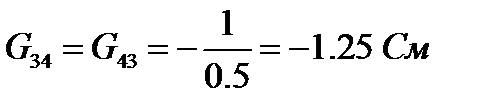
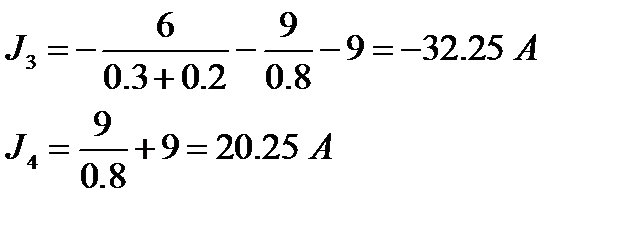
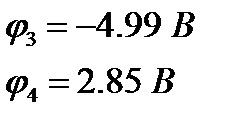
По известным потенциалам узлов можно рассчитать токи в ветвях.

Токи в ветвях с ненулевым сопротивлением определяются с помощью обобщенного закона Ома:

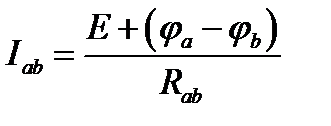. Здесь I_ab - ток ветви ab, текущий от узла a к узлу b; E - ЭДС в ветви (если ЭДС направлена от узла a к узлу b, то она берется со знаком "+", в противном случае со знаком "-"); j_a и j_b - потенциалы узлов a и b соответственно (j_a - j_b = U_ab - падение напряжения вдоль ветви ab). Можно пользоваться и таким правилом для расстановки знаков: E и U входят в формулу со знаками "+", если они со направлены с искомым током, и со знаками "-", если противоположно направлены.

Токи в ветвях с нулевым сопротивлением определяются с помощью 1-го закона Кирхгофа из уравнения, составленного для любого узла, к которому присоединена такая ветвь.

Найдем ток ветви №2:

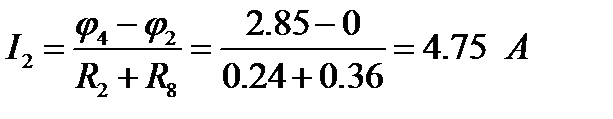, что совпадает с найденной по МКТ величиной.

Аналогичным образом можно найти токи других ветвей:

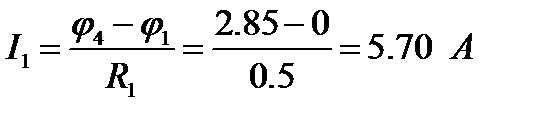
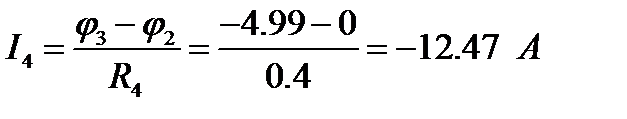
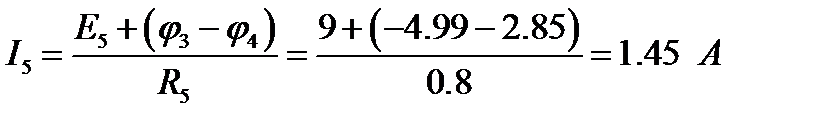
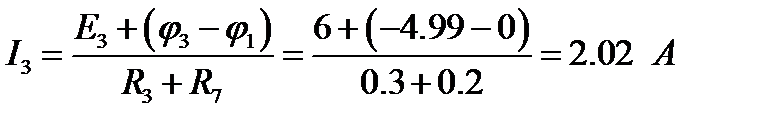
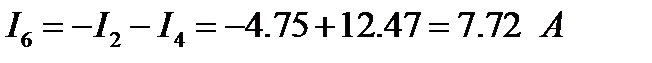
Токи, найденные по МУП, совпадают с токами, найденными по МКТ.