Линейная модель наблюдений имеет вид

Методические указания к выполнению семестрового задания по дисциплине

«ЭКОНОМЕТРИКА»

Для студентов-магистров заочной формы обучения

Введение

В соответствии с учебным планом и рабочей программой по курсу «Эконометрика» каждый студент заочной формы обучения должен выполнить в 1 семестре 1 курса семестровую работу. Изучение этой дисциплины предполагает приобретение студентами опыта построения эконометрических моделей, принятия решения о спецификации и идентификации модели, оценки параметров модели, интерпретации результатов, получения прогнозных оценок.

Семестровая работа содержит 5 заданий, объединённых в рамках единой комплексной задачи. Перед выполнением заданий рекомендуется ознакомиться с соответствующими темами эконометрики:

– линейная модель наблюдений;

– оценка существенности параметров линейной регрессии и корреляции;

– нелинейная связь между переменными;

– интервалы прогноза по линейному уравнению регрессии;

– нелинейная регрессия;

– корреляция для нелинейной регрессии;

– средняя ошибка аппроксимации.

В данных методических указаниях в краткой форме приведены основные понятия перечисленных тем, предложен пример выполнения семестровой работы

В конце методических указаний содержатся варианты заданий и основные статистико-математические таблицы, необходимые для решения задач.

1. Однофакторный регрессионно – корреляционный анализ экономической модели

Уравнение связи двух переменных у и х

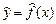
называется уравнением парной регрессии (однофакторной моделью). Переменную 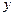при этом называют результативным признаком (эндогенной переменной), а переменную х – факторным признаком (экзогенной переменной).

Пусть имеется n значений переменных у и х: у_i и х_i (i = 1, 2 ,…, n). Разместив на плоскости в прямоугольной системе координат точки (х_i, у_i) с абсциссами х_i и ординатами у_i , получим диаграмму регрессии (поле корреляции). Эти точки будут образовывать облако рассеяния, вытянутое в некотором направлении. По виду поля корреляции формулируют гипотезу о форме связи.

Различают линейные и нелинейные регрессии.

Линейная модель наблюдений имеет вид

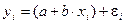, (i = 1, 2,…, n).

Нелинейные регрессии делятся на два класса:

– регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. Например, полиномы разных степеней:

,

,

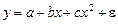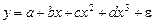равносторонние гиперболы

;

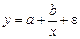– регрессии нелинейные по оцениваемым параметрам. Например,

степенная функция ,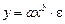

показательная функция ,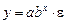

экспоненциальная функция .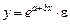

Построение уравнения регрессии сопровождается оценкой его параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК).

Согласно МНК, среди всех возможных значений параметров a и b, претендующих на роль оценок параметров а и b, следует выбрать такую пару a, b, для которой

.

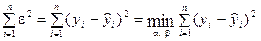Иначе говоря, выбирается такая пара параметров a, b, для которой сумма квадратов оказывается наименьшей.

Для линейных и приводимых к линейным нелинейных уравнений, заданное условие приводит к системе нормальных уравнений

,

.

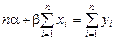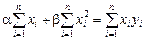решая которую, имеем

, ,

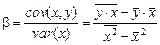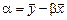где

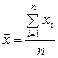– среднее значение последовательности х₁, х₂,…, х_n,

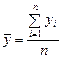– среднее значение последовательности у₁, у₂,…, у_n,

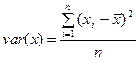– выборочная дисперсия,

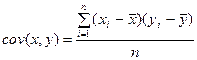– выборочная ковариация.

Для любой точки (х_i, у_i) на диаграмме рассеяния можно записать

,

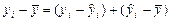где 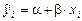– ордината точки линии регрессии (модели), имеющей абсциссу х_i.

Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной.

Возведем обе части последнего представления в квадрат и просуммируем левые и правые части полученных для каждого из i равенств соответственно, получим

.

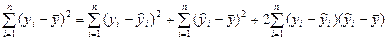Рассмотрев сумму 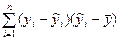более подробно, можно показать, что она в силу системы нормальных уравнений равна нулю.

Тогда

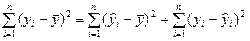(1)

общая сумма квадратов отклонений TSS

сумма квадратов отклонений, объясненная регрессией ESS

остаточная сумма квадратов отклонений RSS

Выражение (1) представляет собой разложение полной суммы квадратов на сумму квадратов, объясненную моделью, и остаточную сумму квадратов.

Долю дисперсии, объясняемую регрессией в общей дисперсии результативного признака у, характеризует коэффициент (индекс) детерминации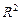

.

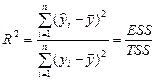Этот коэффициент изменяется в пределах от 0 (при 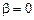, т.е. RSS = TSS) до 1 (при RSS = 0). Таким образом,

.

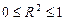Значение 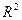тем выше, чем больше доля объясненной моделью суммы квадратов ESS по отношению к полной сумме квадратов TSS.

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции 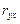для линейной регрессии ( )

,

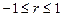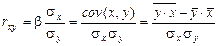где 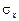, 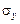– средние квадратические ошибки выборки величин х и у,

и индекс корреляции 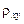– для нелинейной регрессии ( )

.

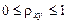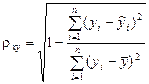Чем ближе значение коэффициента (или индекса) корреляции к единице, тем теснее корреляционная связь.

Заметим, что коэффициент детерминации есть квадрат коэффициента или индекса корреляции.

Средний коэффициент эластичности для рассматриваемой парной модели регрессии рассчитывается по формуле

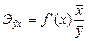
и показывает, на сколько процентов в среднем по совокупности изменится результативный признак у от своей средней величины при изменении факторного признака х на один процент.

Бета–коэффициент показывает, на какую часть величины своего среднего квадратического отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднего квадратического отклонения и задается формулой

.

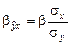После того, как построено уравнение регрессии, необходимо провести оценку значимости как уравнения в целом, так и отдельных его параметров. Оценка значимости уравнения регрессии часто делается с помощью F – критерия Фишера. При этом выдвигается нулевая гипотеза Н₀ о том, что коэффициент регрессии равен нулю (b = 0) и тем самым предполагается, что фактор х не оказывает влияния на результат у.

Существует равенство между числом степеней свободы общей и факторной с остаточной суммами квадратов. Имеем два соответствующих друг другу равенства

,

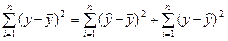n – 1 = 1 + (n –2).

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или дисперсию D на одну степень свободы

, , .

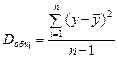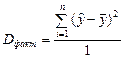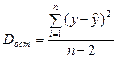Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим F – критерий

.

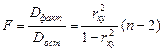Разработаны таблицы (см. таблицы в конце пособия) критических значений F – критерия при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Вычисленное значение F – критерия признается достоверным (отличным от единицы), если оно больше табличного (F_факт>F_табл,). В этом случае нулевая гипотеза Н_о об отсутствии связи признаков отвергается.

Если же его величина окажется меньше табличной (F_факт<F_табл,), то вероятность нулевой гипотезы Н_о выше заданного уровня значимости g (например g = 0,05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым, Н_о не отклоняется.

Оценка значимости уравнения регрессии обычно дается в виде таблицы дисперсионного анализа (табл. 1).

Таблица 1

Источники вариации	Число степеней свободы	Сумма квадратов отклонений	Дисперсия на одну степень свободы	F – отношение
факт	таблич. при a=0,05
Общая	n–1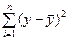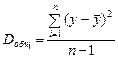
Объясненная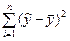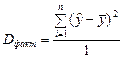
Остаточная	n–2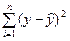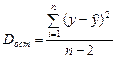

В линейной регрессии обычно оценивается не только уравнение в целом, но и отдельные его параметры. С этой целью по каждому из параметров определяется его стандартная ошибка: m_b, m_a.

Стандартная ошибка коэффициента регрессии определяется по формуле

,

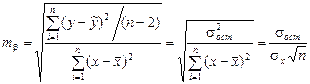где 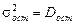– остаточная дисперсия на одну степень свободы

.

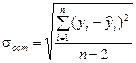Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t – критерия Стьюдента 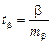, которое затем сравнивается с табличным значением (см. таблицу в конце пособия) при определенном уровне значимости g и числе степеней свободы (n – 2).

Можно показать справедливость равенства .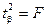

Если фактическое значение t – критерия превышает табличное, то гипотезу о существенности коэффициента можно отклонить.

Границы доверительного интервала коэффициента регрессии b определяются как .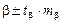

Стандартная ошибка параметра a определяется по формуле

.

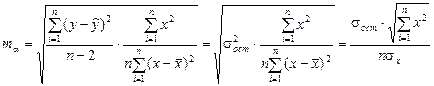Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется t – критерий: 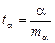, его величина сравнивается с табличным значением при (n –2) степенях свободы и заданном уровне значимости g.

Границы доверительного интервала параметра a определяются как .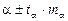

Предельная ошибка D каждого показателя имеет вид:

, .

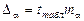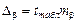Значимость линейного коэффициента корреляции проверяется по величине ошибки коэффициента корреляции:

.

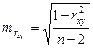При этом, 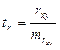– фактическое значение t – критерия Стьюдента.

Данная формула свидетельствует о том, что в парной линейной регресси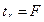и , и 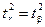. Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности уравнения регрессии.

Если значение 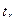значительно превышает табличное значение при заданном уровне значимости g, то коэффициент корреляции существенно отличен от нуля, и построенная модель является достоверной.

Рассмотренная оценка коэффициента корреляции рекомендуется к применению при большом числе наблюдений и если r не близок к +1 или –1.

Фактические значения результативного признака у отличаются от теоретических значений 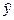, рассчитанных по уравнению регрессии. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели.

Величина отклонений фактических и расчетных значений результативного признака 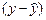по каждому наблюдению представляет ошибку аппроксимации. Их число соответствует объему совокупности. Отклонения 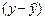несравнимы между собой. Так, если для одного наблюдения 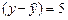, а для другого оно равно 10, то это не означает, что во втором случае модель дает вдвое худший результат. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям.

Чтобы иметь общее представление о качестве модели, из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации –среднее отклонение расчетных значений от фактических:

.

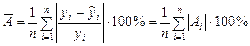Допустимый предел значений 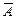– не более 8–10%.

Прогнозное значение у_р определяется путем подстановки в уравнение регрессии 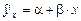соответствующего (прогнозного) значения х_р.

Средняя стандартная ошибка прогноза определяется по формуле:

.

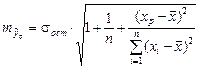Границы доверительного интервала прогноза определяются как 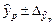, где 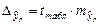– ошибка прогноза.