Нормальное уравнение плоскости

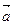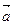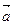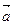Зададим вектор в прямоугольной системе координат, имеет начало в точке О. Через проведем плоскость перпендикулярную к . Произвольную точку плоскости обозначим Q(х, у, z); 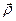- радиус – вектор.

Пусть р = | 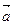| - длина вектора 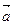, 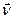- единичный вектор направленный в ту же сторону, что и вектор .

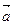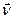= (cosa, cosb, cosg),

где a,b,g - углы, образуемые вектором 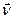с положительным направлением осей х, у, z

Проекция любой точки Q Î p на вектор 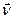, есть величина постоянная, равная р:

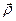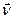( , ) = р (р ³ 0) (10.3)

Получили уравнение плоскости в векторной форме.

В координатах (10.3) записывается:

xcosa +уcosb +zcosg = 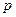, ( 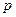³ 0) (10.4)

Это – нормальное уравнение плоскости; где 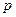– длина перпендикуляра опущенного из начала координат на плоcкость.

Произвольное уравнение в общем виде (10.1) можно привести к нормальному виду, умножив его на число

t = ± 1/ 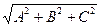, где знак берется противоположным знаку .

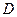Тогда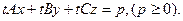

Здесь вектор 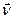= 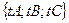единичный ê 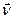ê= 1, его проекции на оси координат равны 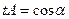; 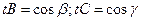. Таким образом

xcosa + уcosb + zcosg = р , (р ³ 0) , т.е. получим уравнение плоскости в нормальном виде.

Из этого уравнения мы можем узнать расположение плоскости относительно системы координат.

Точка М(х, у,z) лежит на плоскости, тогда и только тогда, когда координаты этой точки удовлетворяют уравнению(10.4).

Если же точка не лежит на плоскости, то

хcosa +уcosb +zcosg - р = d

d есть отклонение точки М от плоскости. Отклонение d - есть число (+ 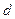), где d - расстояние от точки до плоскости, если точка 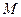и начало координат лежат по разные стороны от плоскости. И 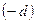, есл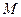и и 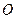лежат по одну сторону от плоскости

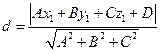. (10.5)

Расстояние от точки до плоскости равно .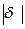

Пример 10.1. Составить уравнение плоскости, проходящей через точку 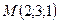перпендикулярно вектору .

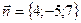Решение. Так как плоскость перпендикулярна вектору 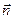, то он является вектором нормали для искомой плоскости. Применяя формулу (10.2), для плоскости, проходящей через заданную точку, получаем 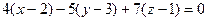. Раскрывая скобки и приводя подобные слагаемые, получаем искомое уравнение плоскости 4x-5y+7z=0 .

Пример 10.2.Дан тетраэдр с вершинами: 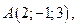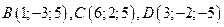. Найти длину высоты, опущенной из вершины 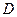на грань .

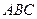Решение.Искомая высота равна расстоянию от точки 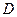до плоскости, проходящей через точки 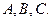Составим уравнение этой плоскости:

.

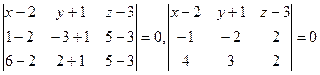Раскрывая определитель по первой строке, получаем 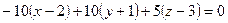. Раскрывая скобки и приводя подобные, получаем .

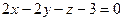По формуле (10.5) находим расстояние от точки 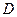до плоскости:

.

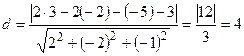Пример 10.3.Составить уравнение плоскости, проходящей через точку М(3;-1;-5) и перпендикулярной плоскостям 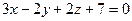и .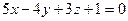

Решение.Так как плоскость перпендикулярна двум данным плоскостям, то ее вектор нормали 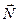также перпендикулярен нормальным векторам 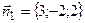и 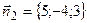. Следовательно,

Далее, используя уравнение плоскости, проходящей через данную точку М(3;-1;-5) перпендикулярно вектору

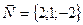, получаем 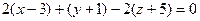, или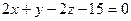

Пример 10. 4. Привести к нормальному виду уравнение плоскости 2х+Зу-6z+21=0. .

Решение. Находим нормирующий множитель (знак которого «минус», поскольку D = 21>0);

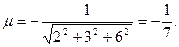
Итак, нормальное уравнение заданной плоскости имеет вид

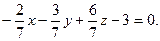
Пример 10.5. Определить расстояние от точки М(3;5;-8) до плоскости 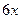—3y + 2z — 28 = 0.

Решение. Используем формулу расстояния от точки до плоскости

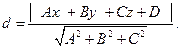
Находим: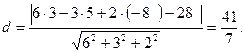

(Результат подстановки отрицателен; таким образом, заданная точка и начало координат лежат по одну сторону от данной плоскости.)

Пример 10.6. Найти уравнение плоскости, проходящей через точку M(2;3;-1) параллельно плоскости

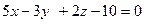
Решение. Напишем уравнение плоскости, проходящей через данную точку:

А(х—2) +В (у—3)+С(z+1) = 0.

Чтобы искомая плоскость была параллельна данной плоскости, необходимо выполнение условия

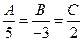
Отсюда следует, что A = 5t, B = -3t, C = 2t. Следовательно, уравнение искомой плоскости примет вид

5t(x-2)-3t(y-3)+2t(z+1)=0,

или

5x-3y+2z+1=0

Нетрудно видеть, что с самого начала можно принять

А = 5, В= —3, С = 2.

Пример 10.7.. Составить уравнение плоскости, проходящей через точку M(2: -1; 5) и перпендикулярной к плоскостям Зх-2y + z+7 = 0 и 5x—4y+3z+ 1=0.

Решение. Запишем уравнение искомой плоскости в виде

A(x-2)+B(y + 1)+C(z - 5)=0.

Так как плоскость перпендикулярна к заданным плоскостям, то должны выполняться условия

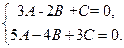Исключив из системы уравнений

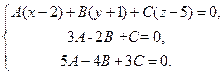ЗА - 2В+С = 0,

коэффициенты A, В, С (пользуемся тем, что система трех линейных однородных уравнений с тремя неизвестными A, В и С имеет ненулевое решение, так как плоскость, удовлетворяющая поставленным условиям, существует всегда), получаем уравнение искомой плоскости в виде

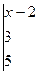
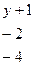
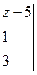=0 или x+2y+z-5=0

Пример 10.8.. Вычислить расстояние между параллельными плоскостями х- 2y -2 z-12 = 0 и х- 2y -2 z-12 .

Решение. На первой плоскости выберем точку M(x;y;z).Две координаты можно выбрать произвольно, а третья определится из уравнения плоскости. Пусть х=0; y=0: тогда z=6. Расстояние между параллельными плоскостями будет равно расстоянию от точки M(0;0;6) до второй плоскости. Воспользуемся формулой расстояния от точки до плоскости (10.5).

Получим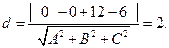

Вопросы для самопроверки

1. Каким характерным признаком отличается уравнение плоскости в декартовой системе координат от уравнений других поверхностей?

2. Как располагается плоскость относительно осей координат, если в ее уравнении отсутствуют те или иные члены?

3. Как определить, по какую сторону от плоскости расположена точка?

4. Приведите формулу вычисления расстояния от точки до плоскости.