Проекції кутів між прямими

Задачі для підготовки до практичних занять:

4.1. Через точку С провести пряму, яка перетинає відрізок АВ та перпендикулярна до нього.

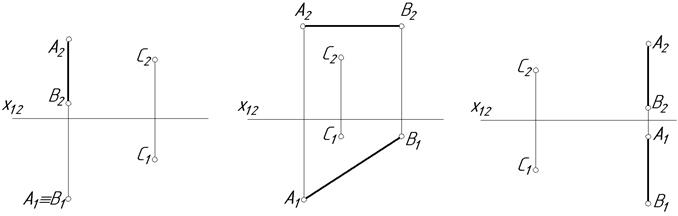
а б в

14.

4.2. Перетнути відрізки АВ і CD прямою яка перпендикулярна до них.

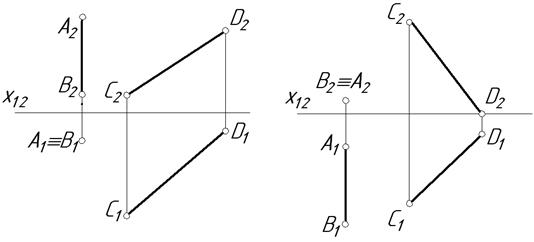
а б

4.4. Визначити відстань між 4.5. Визначити горизонтальну мимобіжними відрізками проекцію точки С, якщо відстань від

АВ та CD. точки С до відрізка АВ дорівнює 20 мм.

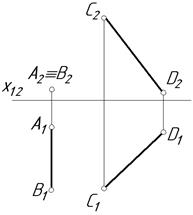
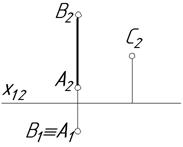
4.6. Задана пряма m, яка паралельна

горизонтальній площині проекцій, та

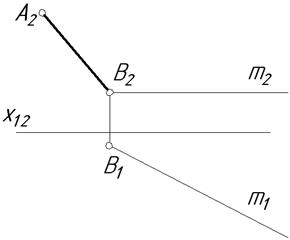фронтальна проекція перпендикулярного

до неї відрізка АВ. Побудувати прямокутник АВCD з основою ВС на

прямій m, виходячи з умови, що довжина

основи рівна 1,5 АВ.

15.

ПЛОЩИНА

Проекції площини

Загальні положення

1. Площина може бути задана (див. рис. 7):

а) трьома точками, які не належать одній прямій (рис. 7, а);

б) прямою і точкою, яка не належить цій прямій (рис. 7, б);

в) двома паралельними прямими (рис. 7, в);

г) двома прямими, що перетинаються (рис. 7, г);

д) плоскою геометричною фігурою (відсіком) – трикутником (рис. 7, д), колом тощо;

е) слідами площини – лініями перетину площини з площинами проекцій (рис. 7, е).

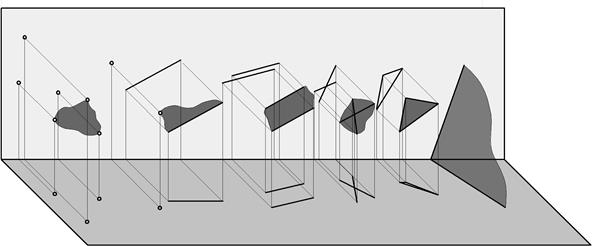
а б в г д е

Рис. 7

2. Проекцію площини задають проекціями її геометричних елементів, які визначають її одним вище вказаних способів.

3. Залежно від положення площини відносно площин проекцій розрізняють (див. рис. 8):

а) площини рівня які паралельні одній з площин проекцій – горизонтальні (рис. 8, б, д), фронтальні, профільні (рис. 8, г);

б) площини проекціювальні які перпендикулярні до однієї з площин проекцій – горизонтально проекціювальні, фронтально проекціювальні (рис. 8, в), профільно проекціювальні;

г) площини загального положення – не паралельні і не перпендикулярні до площин проекцій, тобто довільно нахилені (рис. 8, а).

4. Проекціювальну площину або площину рівня можна задати на комплексному кресленику однією лінією – проекцією сліду.

16.

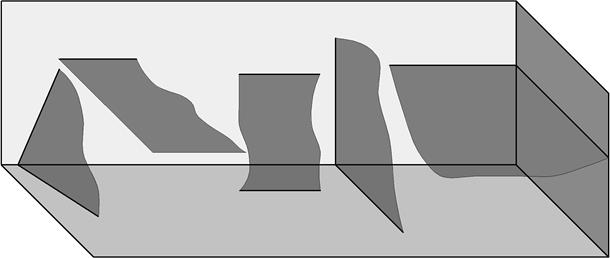
а б в г д

Рис. 8

4. Площину, яка проходить через вісь проекцій, називають осьовою. Якщо вона нахилена до площин проекцій під кутом 45º, то її називають бісекторною.

5. Пряма належить площині, якщо дві її точки належать площині.

6. Точка на будь-якій прямій площині належить цій площині.

7. В площині безліч ліній, але відрізняють так звані головні лінії – лінії рівня та лінії найбільшого нахилу до площин проекцій.

7. Лініями рівня називають прямі, що належать площині і паралельні одній з площин проекцій: горизонталь h, фронталь f і профільна p.

8. Лінії найбільшого нахилу площин до площин проекцій – лінії, що належать площині і перпендикулярні до ліній рівня. Лінія найбільшого нахилу до горизонтальної площини проекцій називається лінією скату.

9. Всі лінії рівня паралельні до відповідних слідів. Сліди площин – нульові лінії рівня (h⁰; f⁰; p⁰).

17.

Задачі для підготовки до практичних занять:

5.1. Задати довільну проекціювальну площину:

а) горизонтальну – двома прямими, які перетинаються;

б) горизонтальну – площину слідами;

в) фронтальну – двома паралельними прямими.

а б в

5.2. Задати довільну профільно проекціювальну площину:

а) двома прямими, які перетинаються;

б) двома паралельними прямими;

в) слідами.

а б в

5.3. Побудувати другу проекцію точки, яка належить заданій площині.

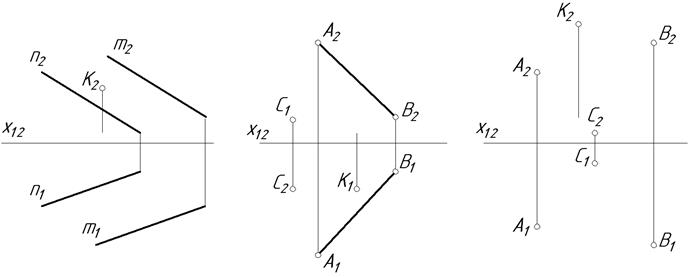
а б в

18.

5.4. Визначити, чи належить відрізок АВ площині.

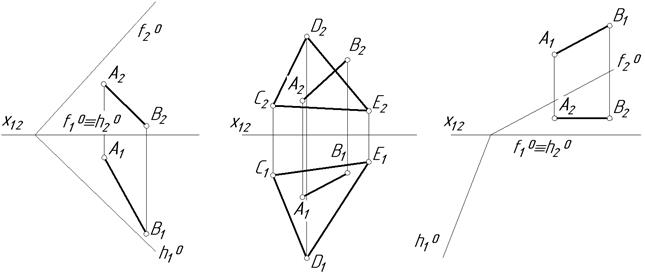
а б в

Аудиторні задачі:

5.5. Визначити, чи належить точка А площині.

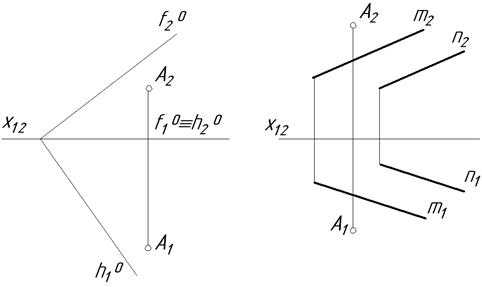
а б

19.

5.6 В заданих площинах побудувати горизонталь, фронталь та лінію найбільшого схилу.

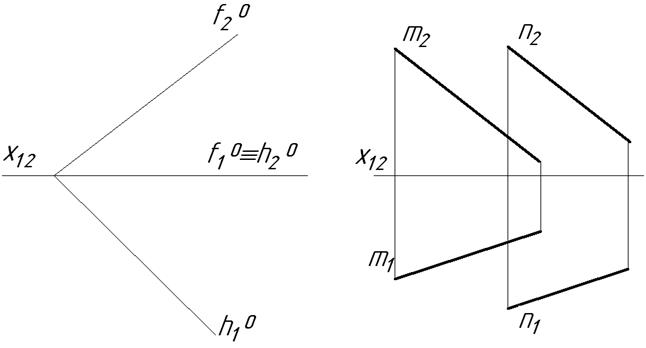
а б

5.7. Знайти проекції відрізка АВ який лежить площині (m||n).

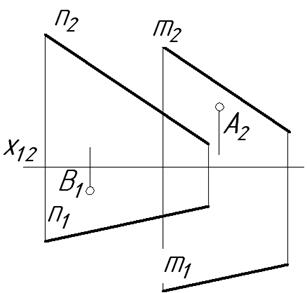
20.

Проекціювальні площини

Загальні положення

Дві площини перетинаються по прямій лінії. Лінія перетину двох проекціювальних площин – проекціювальна. Лінія перетину двох площин, одна з яких проекціювальна – проекціювальна, тобто перпендикулярна до площини проекцій.

Задачі для підготовки до практичних занять:

6.1. Визначити проекції лінії перетину двох площини та видимість елементів геометричних фігур.

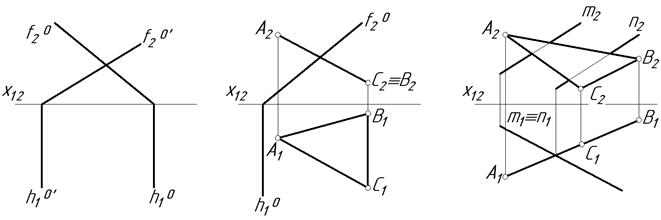
а б в

Аудиторні задачі:

6.2. Побудувати проекції другої площини, якщо відома їх лінія перетину.

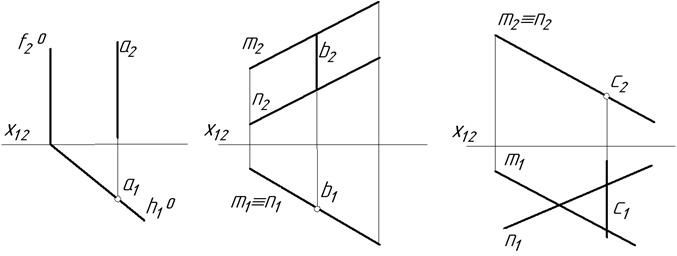
а б в

21.

Перетин прямої з площиною

Загальні положення

1. Алгоритм розв’язання задачі на визначення точки перетину прямої з площиною складається з трьох операцій (див. рис. 9):

а) через задану пряму провести допоміжну проекціювальну площину;

б) побудувати лінію взаємного перетину цієї допоміжної площини з заданою;

в) визначити точку перетину побудованої лінії з заданою.

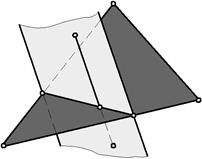
Рис. 9

Якщо пряма або площина проекціювальні, точки перетину визначають безпосередньо на рисунку.

Задачі для підготовки до практичних занять:

7.1. Знайти точку перетину відрізка АВ з проекціювальною площиною.

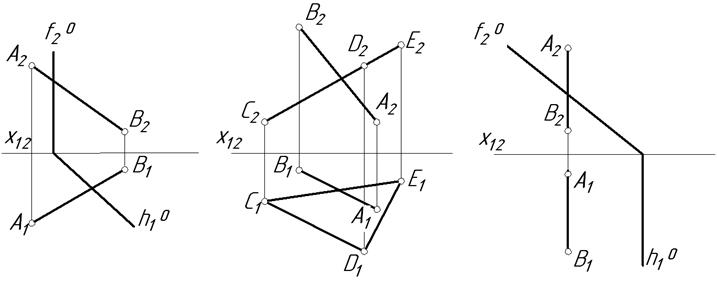
а б в

22.

7.2. Знайти точку перетину відрізка АВ з площиною загального положення.

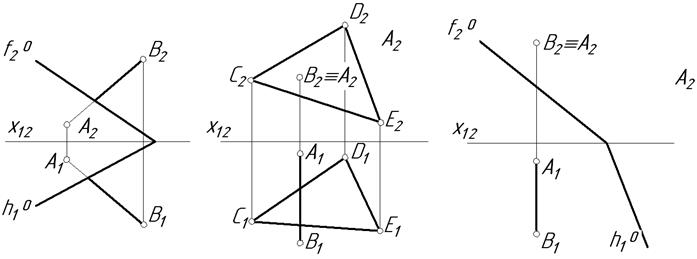
а б <<*>> в

Аудиторні задачі:

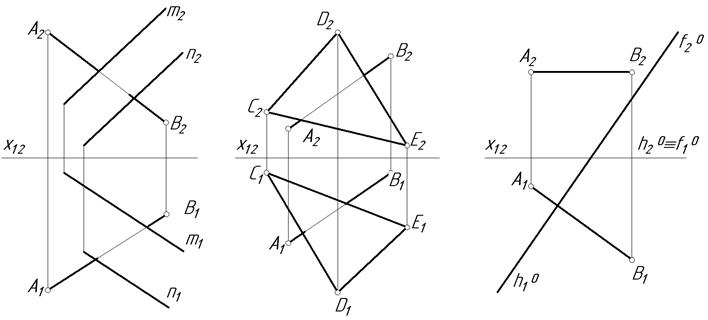7.3. Знайти точку перетину відрізка АВ з площиною загального положення.

а б в

23.