К о н т р о л ь н ы е в о п р о с ы

1. Какое уравнение называется

а) общим уравнением прямой;

б) уравнением прямой в отрезках;

в) уравнением прямой с угловым коэффициентом;

г) каноническим уравнением прямой?

2. Какие уравнения называются параметрическими уравнениями прямой?

3. Каков геометрический смысл коэффициентов каждого из перечисленных в пунктах 1-2 уравнений прямой?

4. Какое уравнение называется

а) векторным уравнением прямой;

б) векторно-параметрическим уравнением прямой?

5. Любую ли прямую можно задать

а) общим уравнением;

б) уравнением в отрезках;

в) уравнением с угловым коэффициентом;

г) каноническим уравнением;

д) параметрическими уравнениями?

6. Сколько существует для заданной прямой

а) общих уравнений;

б) уравнений в отрезках;

в) уравнений с угловым коэффициентом;

г) канонических уравнений;

д) параметрических уравнений?

7. Пусть прямая задана одним из уравнений, перечисленных в пунктах1-2. Как перейти для этой прямой к другим из этих уравнений?

8. Как установить, лежит ли заданная точка М₀(х₀;y₀) на данной прямой (рассмотрите различные способы задания прямой)?

9. Найдите угол между прямыми:

а) A₁x+B₁y+C₁=0 и A₂x+B₂y+C₂=0;

б) Ax+By+C=0 и x=x₀+lt, y=y₀+mt;

в) 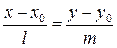и .

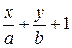(Рассмотрите другие сочетания способов задания прямых).

10. Запишите условия

а) параллельности двух прямых;

б) перпендикулярности двух прямых;

в) пересечения двух прямых;

г) совпадения двух прямых.

(Рассмотрите различные сочетания способов задания двух прямых).

11. Пусть задано уравнение прямой и точка М₀(x₀;y₀). Как вычислить расстояние от точки до прямой (рассмотрите всевозможные способы задания прямой)?

12. Какому условию должны удовлетворять коэффициенты уравнения прямой, которая

а) параллельна оси абсцисс;

б) проходит через начало координат?

13. Пусть прямая задается уравнением вида 5х–7у+с=0.(1) Известно, что точки М₁(x₁;y₁), М₂(x₂;y₂) лежат на этой прямой. Подставив координаты этих точек в уравнение (1), получим с₁= –(5х₁–7у₁) и с₂= –(5х₂–7у₂). Сравните числа с₁ и с₂.

14.Каков геометрический смысл неравенств

а) Ax+By+C >0;

б) Ax+By+C <0;

в) Ax+By+C ³0

г) Ax+By+C £0?

Примеры:

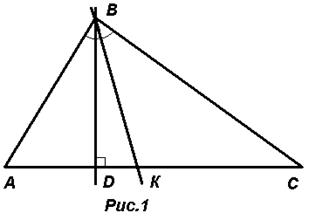
1. Известны вершины треугольника АВC: А(2;4), В(1;3), С(–1;5). Запишите уравнения высоты и биссектрисы, проведенных из вершины В.

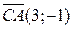Р е ш е н и е: 1) Так как высота ВD перпендикулярна вектору , то ее уравнение можно записать в виде 3х–у+с=0. Для нахождения С используем тот факт, что эта высота проходит через точку В, а значит, координаты точки В должны удовлетворять этому уравнению, поэтому 3·1–1·3+С=0. Тогда С=0. Таким образом, уравнением искомой высоты будет 3х–у=0.

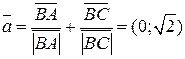2) Очевидно, для искомой биссектрисы направляющим вектором является вектор . Поэтому по точке В и найденному вектору 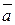можно записать, например, параметрические уравнения биссектрисы ВК: х=1, 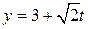или же х=1, =3+t (почему?) (рис.1).

О т в е т : 1) 3х–у=0 – высота ВD, 2) х=1, у=3+t – биссектриса ВК.

2. Дана прямая х=2–3t, у=1+5t. Запишите какое-либо общее уравнение этой прямой.

Р е ш е н и е. Общее уравнение прямой на плоскости имеет вид Ах+Ву+С =0, причем известно, что вектор 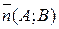будет ортогонален этой прямой. Из заданных параметрических уравнений прямой выписываем координаты направляющего вектора этой прямой (это коэффициенты при t): 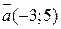. Но тогда вектор 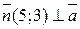. Поэтому общее уравнение имеет вид: 5х+3у+С=0. Для нахождения возьмем на данной прямой, например, точку М₀(2;1) (см. заданные параметрические уравнения): 5·2+3·1+С+0 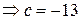. Следовательно, общее уравнение исходной прямой будет 5х+3у-13=0.

О т в е т: 5х+3у-13=0.

3.Вычислите расстояние между параллельными прямыми: х=2t, у=1–3t и х=1–2t, у=4+3t.

Р е ш е н и е: Если прямая задана общим уравнением Ах+Ву+С=0, то расстояние 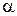от точки М₀(x₀;y₀) до этой прямой вычисляется по известной формуле: 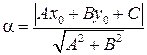(1).

Сведем поставленную задачу к этому случаю. Для любой из этих прямых, например, первой, запишем общее уравнение (см. пример 2): 3х+2у–2=0. Возьмем на другой прямой какую–либо точку, пусть это будет точка М₀(1;4), и далее воспользуемся формулой (1):

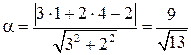(лин.ед.).

О т в е т: 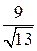лин. ед.

4. Найдите угол между прямым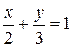и и .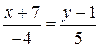

Р е ш е н и е: Выпишем для этих прямых, например, направляющие векторы. Так как первая прямая задана уравнением в отрезка, то вектор 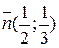или ему коллинеарный вектор 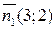являются для этой прямой нормальными. Но тогда вектор 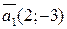будет для этой же прямой направляющим (ведь 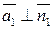). Вторая прямая задана каноническим уравнением, следовательно, вектор, координатами которого являются знаменатели дробей рассматриваемого уравнения, т. е. 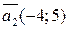, будет для второй прямой направляющим. Угол между прямыми–это меньший из углов, образованных при пересечении соответствующих прямых. Поэтому угол 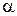между исходными прямыми–это угол между векторами 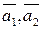, или смежный с ним. Соs =

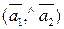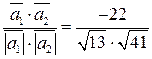= <0, т. е. Угол 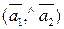–тупой, поэтому

о т в е т: arc Cos .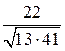

5. Установите, лежит ли точка М₀(1;2) между параллельными прямыми х–3у+7=0 и х-3у+2=0.

Р е ш е н и е: Две различные параллельные прямые разбивают плоскость, в которой они расположены, на три попарно пересекающиеся (если выбросить данные прямые) области. Обозначим их I, II, III (рис.2).

Вначале выясним, лежат ли точка М₀ и первая прямая в одной полуплоскости, определяемой второй прямой. Для этого надо, чтобы координаты точки М₀ и координаты какой либо точки первой прямой (возьмем, например, точку М₁(–7;0)) удовлетворяли одновременно одному из неравенств: х–3у+2>0 или х–2у+2<0. Вычисления показывают, что это выполняется: яПоэтому точка М₀ может попадать или в область I, или в область II. Что бы это установить, выясним, как расположены точки М₀ и вторая прямая относительно первой прямой. На второй прямой берем, например, точку М₂(–2;0) и выясним, принадлежат ли точки М₀ и М₂ одной плоскости, определяемой первой прямой: 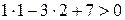, 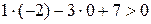. Значит, принадлежат. Но тогда точка М₀ попадает между параллельными прямыми.

Ответ: лежит.

“ПРЯМАЯ
по теме НА ПЛОСКОСТИ”

1. Дана прямая .

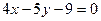1) Укажите какой-либо нормальный вектор заданной прямой.

2) Укажите какой-либо направляющий вектор этой прямой.

3) Запишите какое-либо каноническое уравнение этой прямой.

4) Запишите какие-либо параметрические уравнения этой прямой.

5) Запишите уравнение в отрезках этой прямой.

6) Запишите для этой прямой уравнение с угловым коэффициентом.

7)Вычислите расстояние от точки 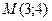до заданной прямой.

8)Лежат ли точки 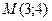, 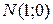в разных полуплоскостях,определяемых данной прямой?

2. Запишите множество, задающее все прямые, ортогональные вектору .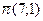
3.Вычислите значение параметра с, при котором прямая 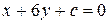проходит через точку .

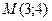4.Найдите значение параметра А, при котором прямая 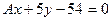параллельна прямой .

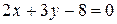5.Для прямой 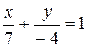укажите величины отрезков, отсекаемых на координатных осях.

6.Дана прямая .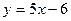

1)Найдите угол, под которым эта прямая пересекает ось 0х.

2)Запишите множество, задающее все прямые, параллельные данной прямой.

7.Для прямой 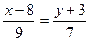запишите какой-либо направляющий вектор.

прямой.

8.Найдите значение параметра 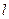, при котором прямая 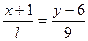перпендикулярна прямой 5x-3y-21=0.

9.Дана прямая 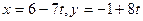. Запишите

1)какое-либо ее общее уравнение;

2)множество, задающее все прямые, параллельные данной прямой.

3)Для заданной прямой установите принадлежит ли ей точка .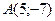

10.Найдите значение параметра 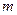, при котором прямая 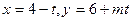параллельна прямой y= - 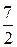x+5.

Лабораторная работа №5

Вариант 1

1. Точка А(9;6) является вершиной квадрата, одна сторона которого лежит на прямой 3х-4у+7=0. Вычислите площадь этого квадрата.

2. Составьте. уравнение биссектрисы того угла между прямыми 2х+5у+7=0 и 5х-2у+3=0, в котором лежит точка .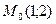

3. Основание равнобедренного треугольника лежит на прямой 3х+у-1=0, боковая сторона – на прямой 4х+3у-13=0. Составьте уравнение другой боковой стороны этого треугольника, зная, что ее расстояние от точки пересечения данных прямых равно 5.

4. Известны вершина А(3;-4) треугольника и уравнения двух его высот: 7х-2у-1=0 и 2х-7у-6=0. Составьте уравнения сторон этого треугольника и уравнение медианы, проведенной из вершины А.

5. Даны уравнения одной из сторон ромба: 3х+5у+1=0 и одной из его диагоналей: х+у-1=0. Запишите уравнения остальных сторон ромба, зная, что диагонали ромба пересекаются в точке О(-1;2).

Вариант 2

1. Вычислите расстояние между прямыми 8х+6у+27=0 и 4х+3у+15=0.

2. Установите, лежит ли точка 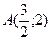внутри треугольника, стороны которого задаются уравнениями 4х+5у-13=0, х+4у-17=0 и 3х+у-7=0.

3. Составьте уравнения прямых, проходящих через точку А(2;-4) и наклоненных к прямой х+5у-7=0 под углом .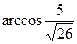

4. Даны две вершины А(-6;2), В(2;-2) треугольника и точка О(1;2) пересечения его высот. Запишите уравнения сторон этого треугольника и уравнение его медианы, проведенной из третьей вершины С.

5. Уравнение одной из сторон квадрата х+3у-5=0. Составьте уравнения остальных сторон квадрата, если О(-1;0) – центр симметрии этого квадрата.

Вариант 3

1. Даны уравнения двух сторон прямоугольника: 2х-у+10=0, х+2у+3=0 и одна из его вершин: А(-1;3). Вычислите площадь этого прямоугольника.

2. Даны две параллельные прямые: 2х-7у+4=0 и 2х-7у-16=0. Установите, лежит ли точка 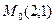между ними.

3. Зная уравнения боковых сторон равнобедренного треугольника: 4х-3у+1=0 и х-7=0, найдите уравнение основания, при условии, что оно проходит через точку А(0;1).

4. Даны вершина В(3;5) равнобедренного треугольника и уравнение х-2у+12=0 его основания. Составьте уравнения боковых сторон этого треугольника, зная, что длина основания треугольника равна 12 .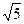

5. Точки А(1;0) и В(4;-1) являются соседними вершинами ромба, уравнение одной из диагоналей х-2у-6=0. Запишите уравнения сторон этого ромба.

Вариант 4

1. Две стороны квадрата лежат на прямых 3х-4у-3=0 и 3х-4у+7=0. Вычислите площадь этого квадрата.

2. Последовательные вершины четырехугольника суть точки 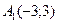, , 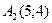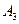(2;1) и 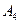(1;-2). Установите, является ли этот четырехугольник выпуклым?

3. Составьте уравнения катетов прямоугольного равнобедренного треугольника, если уравнение гипотенузы 3х-у+5=0, а координаты одной из вершин (2;-5).

4. В треугольнике АВС известны: сторона АВ, заданная уравнением 4х+у-12=0, высота ВН, заданная уравнением х+3у-25=0 и высота 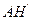, заданная уравнением 3х-5у-9=0. Запишите уравнения остальных сторон этого треугольника и уравнение его медианы, проведенной из вершины С.

5. Уравнение одной из сторон ромба 3х+у+3=0. Точка А(3;-2) является его вершиной, точка О(1;-1) – центром симметрии. Составьте уравнения сторон этого ромба.

Вариант 5

1. Одна сторона квадрата лежит на прямой х-2у+4=0.Точка А(-3;-2) является его вершиной. Вычислите площадь этого квадрата.

2. Составьте уравнение биссектрисы угла между прямыми х-7у+4=0 и 7х+у+6=0, смежного с углом, содержащим точку С(1;1).

3. В равнобедренном треугольнике известны: уравнение основания 3х+у-14=0, уравнение одной из боковых сторон х-5=0. Составьте уравнение второй боковой стороны этого треугольника, если известно, что она проходит через точку Р(1;-2).

4. Составьте уравнение сторон треугольника, зная одну его вершину В(2;-7), а также уравнения высоты 3х+у+11=0 и медианы х+2у+7=0, проведенных из различных вершин.

5. Уравнение одной из сторон прямоугольника х-3у+13=0. Точка О(0;1) является его центром симметрии. Составьте уравнения остальных сторон прямоугольника, зная, что точка А(4;-1) – вершина этого прямоугольника.

Вариант 6

1. Вычислите расстояние между прямыми 3х-4у+11=0 и 3х-4у+6=0.

2. Установите, лежит ли точка М(3;4) внутри треугольника, стороны которого заданы уравнениями: х+у-5=0, х+2у-12=0 и 2х+у-6=0.

3. Основание равнобедренного треугольника лежит на прямой 5х+у+1=0, боковая сторона – на прямой 12х+5у-8=0. Составьте уравнение второй боковой стороны этого треугольника, зная, что ее расстояние от точки пересечения данных прямых равно 7.

4. Известны вершина А(0;3) треугольника АВС и уравнения двух его высот: 2х+у-6=0 и 4х-5у+12=0. Составьте уравнения сторон этого треугольника и уравнение медианы, проведенной из вершины А.

5. Точки А(-2;0) и С(4;2) являются противолежащими вершинами квадрата. Напишите уравнения сторон этого квадрата.

Вариант 7

1. Точка А(-2;1) является вершиной прямоугольника. Две его стороны лежат на прямых 3х-5у-6=0 и 5х+3у+3=0 Вычислите площадь этого прямоугольника.

2. Даны параллельные прямые: х+9у+3=0, х+9у+2=0, х+9у-18=0. Установите, какая из них лежит между двумя другими.

3. Даны: вершина А(3;1) равнобедренного треугольника, уравнение 6х-2у+1=0 его основания , угол 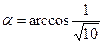при основании. Составьте уравнения боковых сторон этого треугольника.

4. Даны две вершины А(1;4) и В(5;2) треугольника и точка О(2;2) пересечения его высот. Напишите уравнения сторон этого треугольника и уравнение его медианы, проведенной из третьей вершины С.

5. Известны уравнения двух сторон ромба: х-2у+4=0, х-2у-6=0, а также уравнение одной из диагоналей: х+3у-6=0. Напишите уравнения двух других сторон ромба.

Вариант 8

1. Две стороны квадрата лежат на прямых х-2у-1=0, х-2у+4=0. Вычислите площадь этого квадрата.

2. Установите, лежат ли точки N(-2;5), M(3;-1) в вертикальных углах, образованных при пересечении прямых 2х+9у-1=0 и х-3у+16=0.

3. Боковые стороны равнобедренного треугольника лежат на прямых 3х+4у-5=0 и 8х-6у-1=0. Найдите уравнение третьей стороны этого треугольника, если известно, что она проходит через точку Р(1;1).

4. Известны вершина В(3;2) равнобедренного треугольника и уравнение х-у+3=0 его основания. Запишите уравнения боковых сторон, зная, что длина основания этого треугольника равна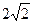

5. Даны уравнение одной из сторон прямоугольника х-у-4=0 и уравнение одной из его диагоналей 2х-у+1=0. Найдите уравнения остальных сторон прямоугольника, если точка О(1;3) является его центром симметрии.

Вариант 9

1. Точка А(1;4) является вершиной квадрата, одна из сторон которого лежит на прямой 3х-у+11=0. Вычислите площадь этого квадрата.

2. Составьте уравнение биссектрисы того угла между прямыми 3х-4у+9=0 и 4х-3у+5=0, в котором лежит точка А(2;4).

3. В равнобедренном прямоугольном треугольнике даны координаты вершины А(3;-7) и уравнение гипотенузы 5х+3у+17=0. Составьте уравнение катетов этого треугольника.

4. В треугольнике АВС известны: сторона АВ, заданная уравнением 3х+у-8=0, высота ВН, заданная уравнением х+3у=0 и высота 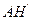, заданная уравнением х-у+4=0. Напишите уравнения остальных сторон этого треугольника и уравнение медианы, проведенной из вершины С.

5. Составьте уравнения сторон ромба АВСD, зная две противолежащие его вершины А(-3;1), С(5;7) и длину диагонали .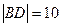

Вариант 10

1. Вычислите расстояние между прямыми 12х-5у+10=0 и 12х-5у-16=0.

2. Установите, лежит ли точка 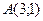внутри треугольника, стороны которого заданы уравнениями 4х-3у-17=0, х+4у-9=0 и 5х+у-7=0.

3. Основание равнобедренного треугольника лежит на прямой 5х+у-7=0, а одна боковая сторона – на прямой х-15=0. Составьте уравнение второй боковой стороны, если известно, что она проходит через точку А(0;1).

4. Даны две вершины А(-4;0) и В(2;-4) треугольника АВС. Медианы треугольника пересекаются в точке Р(0;-1). Составьте уравнения сторон этого треугольника и уравнение высоты, проведенной из вершины С.

5 Составьте уравнения сторон квадрата, зная, что точка А(-4;5) является его вершиной и одна из диагоналей лежит на прямой 7х-у+8=0.

Вариант 11

1. Даны уравнения двух сторон прямоугольника х+5у+13=0, 5х-у+10=0 и одна из его вершин А(-2;3). Вычислите площадь этого прямоугольника.

2. Даны две параллельные прямые 3х+5у-6=0 и 3х+5у+10=0. Установите, лежит ли точка 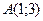между ними.

3. Основание равнобедренного треугольника лежит на прямой х+5у-6=0, одна из боковых сторон – на прямой 5х+12у-17=0. Составьте уравнение второй боковой стороны, что ее расстояние от точки пересечения данных прямых равно 3.

4. Известны вершина А(1;1) треугольника АВС и уравнения двух его высот: 2х+у-12=0 и 4х+у-14=0. Составьте уравнения сторон этого треугольника и уравнение медианы, проведенной из вершины А.

5. Уравнение одной из сторон ромба х+3у-8=0. Точка О(0;1) является его центром симметрии. Составьте уравнения остальных сторон ромба, зная, что точка М(2;-3) лежит на одной из диагоналей.

Вариант 12

1. Две стороны квадрата лежат на прямых 3х-у+1=0 и 3х-у+11=0. Вычислите площадь этого квадрата.

2. Последовательные вершины четырехугольника суть точки: 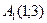, , 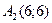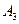(8;-2) и 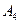(5;2). Установите, является ли этот четырехугольник выпуклым?

3. Основание равнобедренного треугольника лежит на прямой 3х-у+7=0, вершиной является точка А(2;-3). Составьте уравнения боковых сторон этого треугольника, если известно, что угол при основании равен .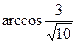

4. Даны две вершины треугольника А(1;5), В(3;-1) и точка О(-3;1) пересечения его высот. Напишите уравнения сторон этого треугольника и уравнение его медианы, проведенной из третьей вершины С.

5. Уравнения двух сторон прямоугольника 2х+3у+11=0 и 3х-2у+23=0. Точка О(1;0) является его центром симметрии. Составьте уравнения двух других сторон этого прямоугольника

Вариант 13

1. Одна сторона квадрата лежит на прямой 2х+3у+14=0.Точка А(-5;3) является его вершиной. Вычислите площадь этого квадрата.

2. Составьте уравнение биссектрисы угла между прямыми 3х-4у+2=0 и 4х-3у+5=0, смежного с углом, содержащим точку С(-1;1).

3. Уравнения боковых сторон равнобедренного треугольника 3х+2у+11=0 и 2х-3у+14=0.Напишите уравнение основания этого треугольника, если известно, что точка А(-1;4) принадлежит основанию.

4. Даны вершина В(4;-2) равнобедренного треугольника и уравнение х-у+2=0 его основания. Составьте уравнения боковых сторон, зная, что длина основания этого треугольника равна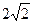

5. Точки А(1;1) и В(2;-1) являются соседними вершинами ромба. Напишите уравнения сторон ромба, зная, что точка М(2;5) лежит на одной из его диагоналей.

Вариант 14

1. Вычислите расстояние между прямыми 5х+12у-15=0 и 5х+12у-2=0.

2. Установите, лежит ли точка 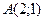внутри треугольника, стороны которого заданы уравнениями 2х-5у+13=0, 3х+2у-9=0 и 4х+9у+7=0.

3. Составьте уравнения прямых, проходящих через точку А(-5;1) и образующих с прямой 2х+у+10=0 угол .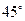

4. В треугольнике АВС известны: уравнение х+2у-9=0 стороны АВ и уравнения у-2=0 и 2х+у-6=0, задающие соответственно высоты ВН и 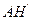. Напишите уравнения остальных сторон этого треугольника и уравнение медианы, проведенной из вершины С.

5. Уравнение одной из сторон прямоугольника 4х+3у-14=0. Запишите уравнение остальных сторон этого прямоугольника, зная, что точка О(1;0) является его центром симметрии, и что точка М(3;4) лежит на одной из диагоналей.

Вариант 15

1. Точка А(1;-3) является вершиной прямоугольника. Две его стороны лежат на прямых х-7у+28=0 и 7х+у+1=0 Вычислите площадь этого прямоугольника.

2. Установите, лежат ли точки А(6;1), В(0;1) в смежных углах, образованных при пересечении двух прямых: х-5у+9=0 и 3х+у-17=0.

3. В равнобедренном треугольнике известны уравнение основания 3х-у+8=0 и уравнение одной из боковых сторон 3х+4у-5=0 Составьте уравнение второй боковой стороны. этого треугольника, если известно, что она проходит через точку Р(1;7).

4. Даны две вершины треугольника А(4;3) и В(-2;-3) треугольника АВС. Медианы треугольника пересекаются в точке Р(2;-1). Составьте уравнения сторон этого треугольника и уравнение высоты, проведенной из вершины С.

5. Даны уравнение х+3у-8=0 стороны ромба и уравнение 2х+у+4=0 его диагонали. Напишите уравнения остальных сторон ромба, зная, что точка М(-9;-1) лежит на стороне, параллельной данной.

ПЛОСКОСТЬ