Интегральная и дифференциальная функции распределения. Вероятность попадания в заданный интервал

Одним из наиболее часто встречающихся распределений является нормальное распределение. Оно играет большую роль в теории вероятностей и занимает среди других распределений особое положение.

Так как нормальному закону подчиняются только непрерывные случайные величины, то это распределение можно задать в виде плотности распределения вероятности.

Определение: Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид

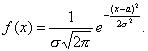
где а и s—некоторые постоянные, называемые параметрами нормального распределения.

Функция распределения F(x) в рассматриваемом случае принимает вид

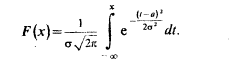
Параметр а- есть математическое ожидание НСВХ, имеющей нормальное распределение, s - среднее квадратическое отклонение, тогда дисперсия равна

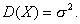
Выясним геометрический смысл параметров распределения а и s. Для этого исследуем поведение функции f(x). График функции f(x) называется нормальной кривой.

Рассмотрим свойства функции f(x):

1°. Областью определения функции f(x) является вся числовая ось.

2°. Функция f{x) может принимать только положительные значения, т. е. f(x}>0.

3°. Предел функции f(x) при неограниченном возрастании |х| равен нулю, т. е. ось ОХ является горизонтальной асимптотой графика функции.

4°. Функция f{x) имеет в точке х = a максимум, равный

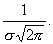
5°. График функции f(x) симметричен относительно прямой х = а.

6°. Нормальная кривая в точках х = а +s имеет перегиб,

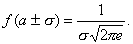
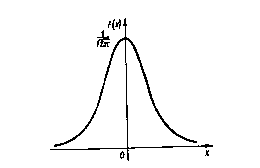
На основании доказанных свойств построим график плотности нормального распределения f(x).

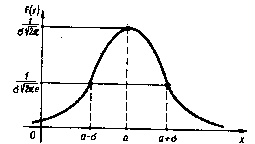
Как видно из рисунка, нормальная кривая имеет колоколообразную форму. Эта форма является отличительной чертой нормального распределения. Иногда нормальную кривую называют кривой Гаусса.

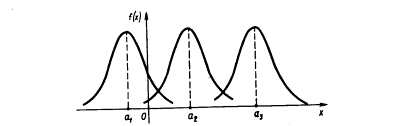
При изменении параметра а форма нормальной кривой не изменяется. В этом случае, если математическое ожидание (параметр а) уменьшилось или увеличилось, график нормальной кривой сдвигается влево или вправо .

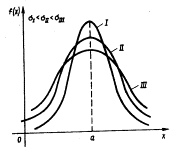
При изменении параметра s изменяется форма нормальной кривой. Если этот параметр увеличивается, то максимальное значение функции f(x) убывает, и наоборот. Так как площадь, ограниченная кривой распределения и осью Ох, должна быть постоянной и равной 1, то с увеличением параметра кривая приближается к оси Ох и растягивается вдоль нее, а с уменьшением s кривая стягивается к прямой х=а .

Использование формул f(x) и F(x) для практических расчетов затруднительно. Но решение задач по этим формулам можно упростить, если от нормального распределения с произвольными параметрами а и s перейти к нормальному распределению с параметрами а=0, s = 1.

Функция плотности нормального распределения f(x) с параметрами а=0, s =1 называется плотностью стандартной нормальной случайной величины и ее график имеет вид:

Функция плотности и интегральная функция стандартной нормальной СВ будут иметь вид:

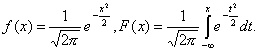
Для вычисления вероятности попадания СВ в интервал (a, b) воспользуемся функцией Лапласа: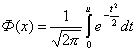

Перейдем к стандартной нормальной случайной величине

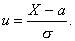
Тогда

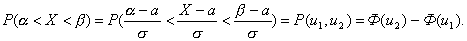
Значения функции Ф(u) необходимо взять из таблицы приложений "Таблица значений функции Ф(х)"

Библиография.

[1] РМГ 29-99 «Метрология. Основные термины и определения»

[2] ГОСТ 8.009-84 «Нормируемые метрологические характеристики средств измерений»

[3] ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования».

[4] ГОСТ 8.050-73 «Нормальные условия выполнения линейных и угловых измерений»

[5] Яворский Б. М. Физика: Для школьников старших классов и поступающих в вузы.\: Учеб. пособие – М.: Дрофа, 2002 – 800с.

[6] Письменный Д. Т. Конспект лекций по высшей математике. 1 часть. М.: Айрис-пресс, 2004. - 288 с.