Порядок оценивания линейной модели множественной регрессии методом наименьших квадратов (МНК) в Excel
(*)
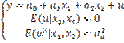Модель (*) – линейная эконометрическая модель в виде изолированных уравнений с несколькими объясняющими переменными или моделями линейной множественной регрессии.
В этой модели две экзогенные переменные x1, x2 и одна эндогенная переменная y. Спецификация (*) содержит четыре параметра: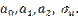 
Пусть известны значения экзогенных и эндогенных переменных модели (*):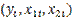 
при t=1, 2, …, n.
Порядок оценивания модели (*) состоит из следующих шагов.
Шаг 1. В столбце А листа Excel с первой строчки расположить значения эндогенной переменной y. В столбцах B и C, начиная с первой строчки, записать значения экзогенных переменных соответственно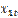 
и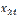 
.
| A | B | C | D | E | F | G | |
| y1 | X11 | X21 | |||||
| Y2 | X12 | X22 | |||||
| … | … | … | … | ||||
| n | yn | X1n | X2n | ||||
| n+1 | |||||||
| n+2 | |||||||
| n+3 | |||||||
| n+4 | |||||||
| n+5 |
Шаг 2. Активировать ячейку с адресом А(n+1) и на стандартной панели инструментов щелкнуть мышью кнопку вставки функций (fx).
Шаг 3. В диалоговом окне «Категория» выбрать «Статистические»; в диалоговом окне «Выберите функцию» - «Линейн»; щелкнуть мышью по кнопке ОК.
Шаг 4. В строчке «Известные_значения_y» диалогового окна указать (латиницей!) адрес А1:Аn диапазона значений эндогенной переменной yt, а в строчке «Известные_значения_х» - адрес B1:Cn диапазона известных значений предопределенных переменных x1,x2.
Шаг 5. В строчку «Конст» диалогового окна занести (кириллицей!) слово «истина», либо цифру 1.
Шаг 6. В строчку «Статистика» диалогового окна занести слово «истина» или цифру 1 и щелкнуть мышью по кнопке ОК.
Шаг 7. Выделить мышью диапазон ячеек A(n+1):C(n+5).
Шаг 8. Щелкнуть мышью по строке формул.
Шаг 9. Нажать клавиши Ctrl + Shift + Enter.
В итоге в выделенном диапазоне ячеек появятся результаты оценивания модели (*).
| A | B | C | D | E | F | G | |
| y1 | X11 | X21 | |||||
| Y2 | X12 | X22 | |||||
| … | … | … | … | ||||
| n | Yn | X1n | X2n | ||||
| n+1 |  |  |  | ||||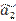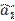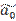
| n+2 |  |  |  | ||||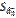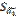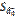
| n+3 | 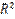 | 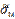 | # Н/Д | ||||
| n+4 | F | 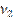 | # Н/Д | ||||
| n+5 | 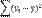 | 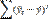 | # Н/Д |
Итак, модель будет выглядеть:
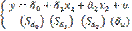
Последствия гетероскедастичности. Тест Голдфелда-Квандта.
Последствия: истинная гетеро-ть не приводит к смещению оценок коэффициентов регрессии; гетеро-ть увеличивает дисперсию распределения оценок коэффициентов; гетеро-ть вызывает тенденцию к недооценке стандартных ошибок коэффициентов при использовании МНК.
Тест Г-К позволяет проконтролировать равенство дисперсий случайных возмущений.
Алгоритм теста:
1) сформировать служебную переменную pi=|x1i|+|x2i|+…+|xki|
2) упорядочить уравнения наблюдений в порядке возрастания переменной pi
3) разбить полученные уравнения примерно на 3 равные части
4) оценить модели по первой и последней частям уравнений наблюдений и вычислить для них ESS (дисперсии)
5) вычислить статистики GQ=ESS1/ESS2 и GQ^-1
6) найти значение Fкрит (через функцию FРАСПОБР)
7) сравнить полученные статистики с Fкрит. Если GQ<= Fкрит и GQ^-1<=Fкрит, то остаток в модели гомо-чен.