Квазиньютоновские методы

В основе квазиньютоновских методов лежит идея восстановления квадратичной аппроксимации функции по значениям ее градиентов. Это позволяет, не прибегая к вычислению матриц вторых производных, разработать методы, обладающие достоинствами метода Ньютона.

Вид итерации квазиньтоновских методов имеет общую структуру

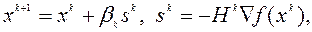(5.10.1)

где матрица 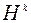пересчитывается рекуррентно таким образом, что

,

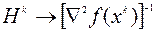если и не на всем пространстве 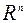, то хотя бы в подпространстве меньшей размерности.

Градиент квадратичной функции (5.9.1) задается выражением:

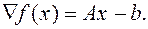(5.10.2)

Для произвольного вектора 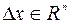разность градиентов 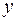, согласно (5.10.2), удовлетворяет соотношению

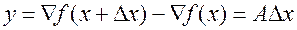. (5.10.3)

При 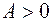, в силу (5.10.3), справедливо равенство

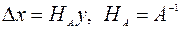. (5.10.4)

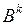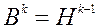В квазиньютоновских методах пересчитываются матрицы либо , где , таким образом, что для них удовлетворяются квазиньютоновские соотношения (5.10.3), (5.10.4), а в качестве векторов 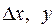берутся векторы

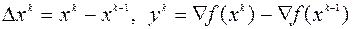, (5.10.5)

где 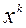- точки, генерируемые процессом (5.10.1).

Произвольную формулу перерасчета матриц 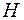или 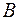, которые после пересчета удовлетворяют квазиньютоновским соотношениям (5.10.3), (5.10.4), будем обозначать 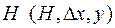и 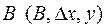соответственно, при этом, если рассчитываются матрицы 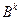, то для использования в (5.10.1) необходимо получить . Формула пересчета матриц Девидона-Флетчера-Пауэлла (DFP) имеет вид

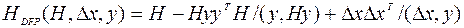. (5.10.6)

В современных вычислительных алгоритмах пересчитываются не матрицы 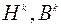, а их треугольные разложения, что при расчете матриц 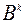, позволяет избежать трудоемкой операции обращения матриц.

Выпишем общую схему метода квазиньютоновского типа

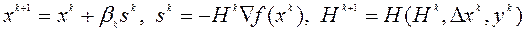, (5.10.7)

,

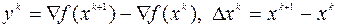где задается начальная точка 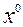и матрица 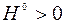. Величины шагов спуска 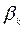удовлетворяют условию точного одномерного спуска

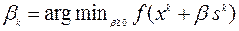, (5.10.8)

либо условию (5.4.8).