Диференціальні рівняння. Числові ряди. Теорія ймовірностей
Завдання до контрольної роботи № 2
1. Завдання.Обчислити визначені інтеграли:
1. 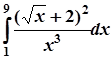 ; 6.
; 6. 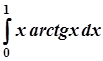 ;
;
2. 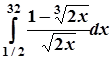 ; 7.
; 7. 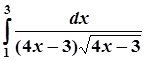 ;
;
3. 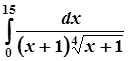 ; 8.
; 8. 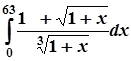 ;
;
4. 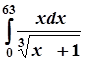 ; 9.
; 9. 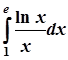 ;
;
5. ; 10. .
2. Завдання.Обчислити площі областей, обмежених заданими лініями:
1. 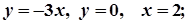
2. 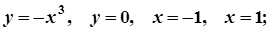
3. 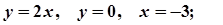
4. 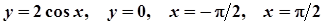
5. 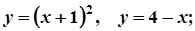
6. 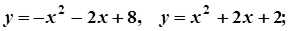
7. 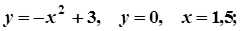
8. 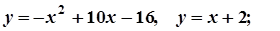
9. 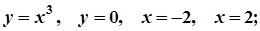
10. 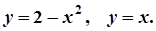
3.Завдання. Обчислити невласні інтеграли, або довести їх розбіжність:
1. 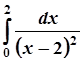 ; 6.
; 6. 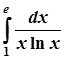 ;
;
2. 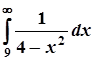 ; 7.
; 7. 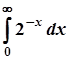 ;
;
3. 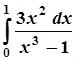 ; 8.
; 8. 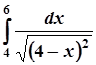 ;
;
4. 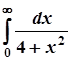 ; 9.
; 9. 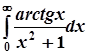 ;
;
5. ; 10. .
4. Завдання.Дослідити на збіжність дані числові ряди:
1. а) 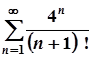 ; б)
; б) 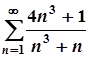 ;
;
2. а) 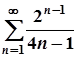 ; б)
; б) 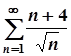 ;
;
3. а) 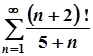 ; б)
; б) 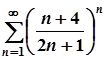 ;
;
4. а) 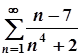 ; б)
; б) 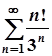 ;
;
5. а) 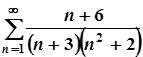 ; б)
; б) 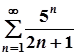 ;
;
6. а) 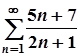 ; б)
; б) 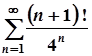 ;
;
7. а) 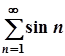 ; б)
; б) 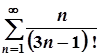 ;
;
8. а) 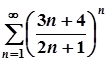 ; б)
; б) 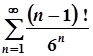 ;
;
9. а) 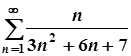 ; б)
; б) 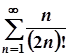 ;
;
А) ; б) .
5. Завдання.З’ясувати чи є даний ряд абсолютно збіжним, умовно збіжним, або розбіжним.
1. 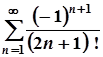 ; 6.
; 6. 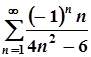 ;
;
2.  ; 7.
; 7. 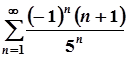 ;
;
3. 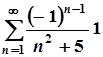 ; 8.
; 8. 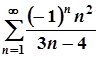 ;
;
4. 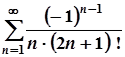 ; 9.
; 9.  ;
;
5. ; 10. .
6. Завдання.Розв’язати диференціальні рівняння першого порядку:
1. а) 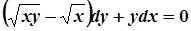 ; б)
; б) 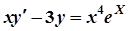 ;
;
2. а) 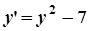 ; б)
; б) 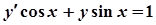 ;
;
3. а) 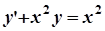 ; б)
; б) 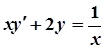 ;
;
4. а) 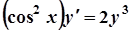 ; б)
; б) 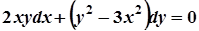 ;
;
5. а) 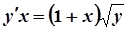 ; б)
; б) 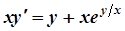 ;
;
6. а) 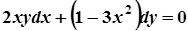 ; б)
; б) 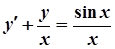 ;
;
7. а) 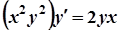 ; б)
; б) 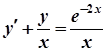 ;
;
8. а) 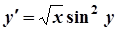 ; б)
; б) 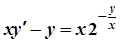 ;
;
9. а) 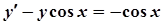 ; б)
; б) 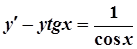 ;
;
А) ; б) .
7. Завдання. Розв’яжіть задачу: знайти криву, що проходить через точку М(а;в), якщо кутовий коефіцієнт дотичної в будь-якій точці кривої дорівнює
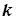 , коли
, коли 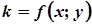 .
.
1. 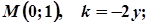 6.
6. 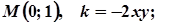
2. 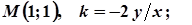 7.
7. 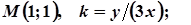
3. 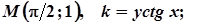 8.
8. 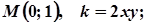
4. 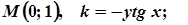 9.
9. 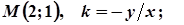
5. 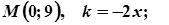 10.
10. 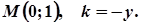
8. Завдання.Розв’язати задачу Коші для лінійного однорідного диференціального рівняння другого порядку:
1. 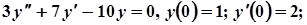
2. 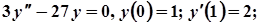
3. 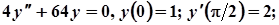
4. 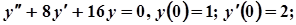
5. 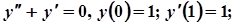
6. 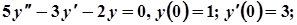
7. 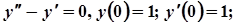
8. 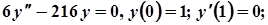
9. 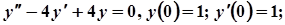
10. .
9. Завдання.Розв’яжіть лінійне неоднорідне рівняння зі спеціальною правою частиною:
1. 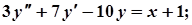 6.
6. 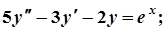
2. 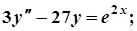 7.
7. 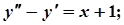
3. 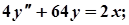 8.
8. 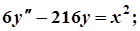
4. 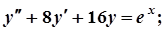 9.
9. 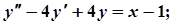
5. 10. .
10. Завдання.Розв’яжіть задачу:
1.Студент знає 20 питань з 25 питань програми. Екзаменатор задає йому три питання. Знайти ймовірність того, що студент знає всі три питання.
2.Серед 100 електроламп 5 зіпсованих. Яка ймовірність того, що взяті навмання 3 лампи будуть справними?
3.Правління підприємства складається з дев`яти осіб. Скільки можна скласти варіантів обрання з їх числа трьох керівників: президента, директора та комерційного директора.
4.У малому підприємстві працюють чотири жінки та п`ять чоловіків. Випадковим способом дві особи запізнились. Знайти ймовірність того, що одна з цих осіб жінка, а друга - чоловік.
5.До профкому обрано семеро осіб, з яких потрібно обрати голову профкому та його заступника. Скількома способами це можливо зробити.
6.Студент забув останні три цифри потрібного телефону, але він пам`ятає, що всі три цифри є різні, тому вибирає їх навмання. Знайти ймовірність того, що набрані цифри вірні.
7.В урні п`ятнадцять червоних, дев`ять синіх та шість зелених куль однакового розміру. Навмання беруть шість куль. Яка ймовірність того, що будуть взяті одна зелена, дві сині та три червоні кулі.
8. Із колоди карт (32 карти) навмання взято одну. Яка ймовірність того, що це дама, якщо відомо, що взято карту червоної масті?
9. В урні 10 білих, 15 чорних, 20 блакитних та 25 червоних куль однакового розміру. Навмання взято одну кулю. Знайти ймовірність того, що ця куля буде біла або чорна.
10.У ящику перебувають 15 м'ячів, з яких 9 нових. Для тренування спортсмен навмання бере три м'ячі. Яка ймовірність того, що вони всі нові?
СПИСОК ЛІТЕРАТУРИ
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1980.
2. Бугров Я.С., Никольский С.М. Высшая математика. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1980.
3. Данко П.Е., Попов А.Г., Кожевников Т.Я. Высшая математика в упражнениях и задачах. – М.: Наука, 2000, ч. 1,2.
4. Дубовик В.П., Юрик І.І. Вища математика. – Київ, “А.С.К.”, 2005. – 648 с.
5. Дюженкова Л.І., Дюженкова О.Ю., Михалін Г.О. Вища математика.
6. Задачи и упражнения по математическому анализу для втузов / Под ред.
Б.П. Демидовича. – М.: Физматгиз, 1978.
7. Кагадій Л.П., Павленко А.В., Чуднов К.У. Лінійна алгебра та аналітична геометрія. Ч. 1,2: Конспект лекцій. – Дніпропетровськ, НМетАУ. – 2004.
8. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1980.
9. Кулініч Г.Л., Максименко Л.О., Плахотник В.В., Призва Г.Й. Вища математика. Основні означення, приклади і задачі. – К.: Либідь, 1994.
10. Маркович Е.С. Курс вищої математики з елементами теорії ймовірностей і
математичної статистики: Навч. посібник для вузів. - 2-е вид., перераб. і доп.:
Вища. шк., 1972. – 480 с.
11. Проскуряков И.В. Сборник задач по линейной алгебре. – М.: Наука, 1984.
12. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. –
М.: Наука, 1985, т. 1, 2.
13. Пискунов Н.С. Дифференциальное и интегральное исчисление: Підручник в
2-х томах, т. I. – М.: Інтеграл – Прес, 2002. – 416 с.
14. Рудавський Ю.К., Костробій П.П. Лінійна алгебра та аналітична геометрія. –
Львів, 1999.
15. Соколенко О.І., Новик Г.А. Вища математика в прикладах і задачах. – К.:
”Либідь”, 2001 р.
16. Шипачьов В.С. Основи вищої математики. – М.: Вища школа, 1989.
ЗМІСТ
| ЗАГАЛЬНІ РЕКОМЕНДАЦІЇ СТУДЕНТУ-ЗАОЧНИКУ ПО РОБОТІ НАД ДИСЦИПЛІНОЮ “ВИЩА МАТЕМАТИКА”……………. | |
| 1. ПРОГРАМА ДИСЦИПЛІНИ “ВИЩА МАТЕМАТИКА” (1 СЕМЕСТР)… | |
| ДОВІДКОВИЙ МАТЕРІАЛ………… …………………………….……..…. | |
| КОНТРОЛЬНА РОБОТА №1 … …………………………………….…….. | |
| 2. ПРОГРАМА ДИСЦИПЛІНИ “ВИЩА МАТЕМАТИКА” (2 семестр)...….. | |
| ДОВІДКОВИЙ МАТЕРІАЛ… ……………..……………………………...… | |
| КОНТРОЛЬНА РОБОТА №2… ………………………………….…..……. | |
| СПИСОК ЛІТЕРАТУРИ…………………………………………………..….…. |
Підписано до друку 28.03.2013. Формат 60х84 1/16. Папір друк. Друк плоский.
Облік.-вид. арк. 2,76. Умов. друк. арк. 2,72. Тираж 100 пр. Замовлення №
Національна металургійна академія України
49600, Дніпропетровськ-5, пр. Гагаріна, 4
______________________________________
Редакційно-видавничий відділ НМетАУ
