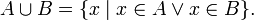Дайте определение объединения множеств. Приведите пример. Поясните с помощью диаграмм Эйлера

Ответы к экзамену по высшей математике.

1) Что называют множеством, элементом множества?

Мно́жество — одно из ключевых понятий математики, в частности, теории множеств и логики.

Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть не сводимое к другим понятиям, а значит и не имеющее определения. Однако, можно дать описание множества, например в формулировке Георга Кантора: «Под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M).»

Другая формулировка принадлежит Бертрану Расселлу: «Множество есть совокупность различных элементов, мыслимая как единое целое». Также, возможно косвенное определение через аксиомы теории множеств.

В математической логике и дискретной математике часто употребляемый синоним множества — алфавит.

Множество может быть замкнутым и незамкнутым, полным и пустым, упорядоченным и неупорядоченным, счётным и несчётным, конечным и бесконечным. Более того, как в наивной, так и в формальной теориях множеств любой объект обычно считается множеством.

Элемент множества -Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами латинского алфавита, его элементы — строчными. Если а — элемент множества А, то записывают а ∈ А (а принадлежит А). Если а не является элементом множества А, то записывают а ∉ А (а не принадлежит А).

2) Какие множества называются счётными (несчётными)?

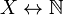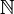Счетное множество -В теории множеств, счётное мно́жество есть бесконечное множество, элементы которого возможно пронумеровать натуральными числами. Более формально: множество X является счётным, если существует биекция (отображение) , где обозначает множество всех натуральных чисел. Другими словами, счётное множество — это множество, равномощное множеству натуральных чисел.

Счётное множество является «наименьшим» бесконечным множеством, то есть в любом бесконечном множестве найдётся счётное подмножество. Мощность множества всех натуральных чисел обозначается символом 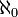(произносится: "алеф-нуль").

СВОЙСТВО:

1. Любое подмножество счётного множества не более чем счётно (т.е. конечно или счётно).
2. Объединение конечного или счётного числа счётных множеств счётно.
3. Прямое произведение конечного числа счётных множеств счётно.
4. Множество всех конечных подмножеств счётного множества счётно.
5. Множество всех подмножеств счётного множества континуально и, в частности, не является счётным.

Счётные множества - !Примеры!

• Простые числа;
• Натуральные числа;
• Целые числа;
• Рациональные числа;
• Алгебраические числа;
• Кольцо периодов;
• Вычислимые числа;
• Арифметические числа;
• Множество всех конечных слов над конечным или счётным алфавитом;
• Любое бесконечное семейство непересекающихся открытых интервалов на действительной оси;
• Множество всех прямых на плоскости, каждая из которых содержит хотя бы 2 точки с рациональными координатами;
• Любое бесконечное множество точек на плоскости, все попарные расстояния между элементами которого рациональны.

Несчетное множество - такое бесконечное множество, которое не является счётным. Таким образом, любое множество является либо конечным, либо счётным, либо несчётным.

Несчётные множества- !Примеры!

• Вещественные числа;
• Комплексные числа;
• Числа Кэли.

3) Какие способы задания множества Вам известны?

Существуют два основных способа задания множеств: перечисление и описание его элементов. Перечисление состоит в получении полного списка элементов множества, а описание заключается в задании такого свойства, которым элементы данного множества обладают, а все остальные нет.
Конечные множества можно задавать обоими способами, причем выбор того или иного способа зависит от удобства задания и дальнейшей работы с множеством. Бесконечные множества можно задавать только с помощью описания.
Георг Кантор определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Эти объекты назвал элементами множества. Множество объектов, обладающих свойством A(x), обозначил 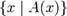. При этом, A(x) называется характеристическим свойством множества.
Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.
Так как теория множеств, фактически, используется как основание и язык всех современных математических теорий в 1908 г. теория множеств была аксиоматизирована независимо Бертраном Расселем и Эрнстом Цермело. В дальнейшем многие исследователи пересматривали и изменяли обе системы, в основном сохранив их характер. До сих пор они всё ещё известны как теория типов Рассела и теория множеств Цермело. В настоящее время, теорию множеств Кантора принято называть наивной теорией множеств, а вновь построенную аксиоматической теорией множеств.

4) Какие отношения между множествами Вы знаете?

Два множества A и B могут вступать друг с другом в различные отношения.
A включено в B, если каждый элемент множества A принадлежит также и множеству B:

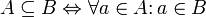
A равно B, если A и B включены друг в друга:

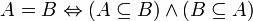
A строго включено в B, если A включено в B, но не равно ему:

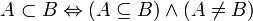
Дайте определение объединения множеств. Приведите пример. Поясните с помощью диаграмм Эйлера.

Объедине́ние мно́жеств (тж. су́мма или соедине́ние) в теории множеств — множество, содержащее в себе все элементы исходных множеств. Объединение двух множеств A и B обычно обозначается 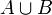, но иногда можно встретить запись в виде суммы A + B.

Объединение двух множеств

Пусть даны два множества A и B. Тогда их объединением называется множество