Передаточные функции импульсных АСУ

Представим структурную схему импульсной системы в виде, показанном на рис. 1.39.

Рис. 1.39. Структурная схема импульсной АСУ

Обычно при анализе АСУ рассматривают передаточные функции разомкнутых и замкнутых систем, а также передаточную функцию ошибки.

Передаточной функцией разомкнутой импульсной системы называют отношение изображений в смысле дискретного преобразования Лапласа выходного и входного импульсных сигналов при нулевых начальных условиях

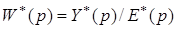, (1.43)

Аналогично

.

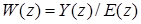Основная задача состоит в определении W(z) по известной W_ПНЧ(z). Эту задачу решают в такой последовательности:

1. Находят функцию веса ПНЧ

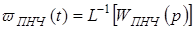. (1.44)

2. По функции веса находят аналитическое выражение для соответствующей дискретной функции веса .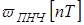

3. Выполнив z-преобразование над 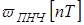, определяют

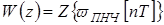. (1.45)

Передаточная функция замкнутой системы по заданию

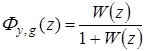, (1.46)

причем

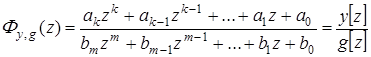. (1.47)

Передаточная функция ошибки

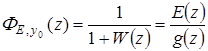. (1.48)

Зная эту передаточную функцию, можно найти дискретную функцию ошибки .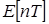

Пример. Определить передаточные функции импульсной системы, если

.

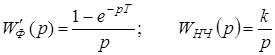Решение. Передаточная функция приведенной непрерывной части

.

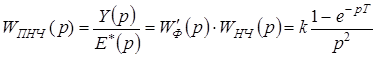Передаточная функция разомкнутой системы

.

.

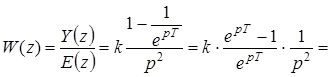
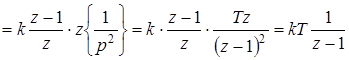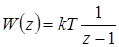Основная передаточная функция

.

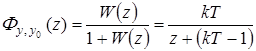Передаточная функция ошибки

.

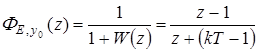Устойчивость и качество дискретных систем

Условия устойчивости

Определения устойчивости непрерывных систем в основном применимы и к импульсным системам. Основная формулировка устойчивости такова: импульсная система устойчива, если ее собственное движение с течением времени затухает.

Решение разностного уравнения

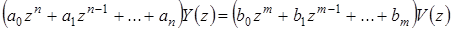, (1.49)

описывающего динамику замкнутой системы, состоит из двух частей

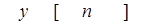, (1.50)

где первая часть определяет свободное движение, а вторая – вынужденное движение.

Решение для дискретной функции y[nT] можно представить в виде суммы свободной и вынужденной составляющих

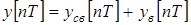. (1.51)

При оценке устойчивости ИАСУ, как и в непрерывной системе, исследуется свободное движение. Оно может быть найдено при решении однородного разностного уравнения (без правой части)

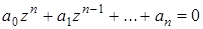, (1.52)

называемого характеристическим уравнением замкнутой ИАСУ. Это же уравнение можно получить и по передаточной функции замкнутой системы K_з(z), приравняв нулю ее знаменатель

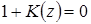. (1.53)

Решение уравнения (1.52) находим в виде

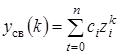, (1.54)

где c_i – постоянные коэффициенты, z_i – корни характеристического уравнения.

Для устойчивости ИАСУ необходимо и достаточно, чтобы выполнялось условие

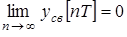. (1.55)

Это возможно, когда все корни характеристического уравнения z_i будут по модулю меньше единицы. Таким образом, условием устойчивости является соотношение

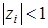. (1.56)

Графически это условие можно интерпретировать, преобразовав р-плоскость в z-плоскость. Так как 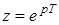, то полагая p = jw, что соответствует мнимой оси, получим 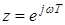, что является окружностью единичного радиуса (рис. 1.40, а).

Эта связь указывает на следующее соответствие корней z_i и p_i:

при p_i = 0 z_i = 1;

если Re p_i < 0, то | z_i | < 1.

р

Отсюда вытекает математическая формулировка условия устойчивости: импульсная система устойчива, если все корни характеристического уравнения замкнутой системы (1.52) лежат внутри круга единичного радиуса с центром в начале координат комплексной плоскости z (рис. 1.40, б).

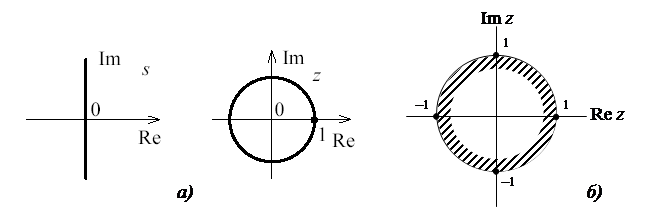Если хотя бы один корень лежит на окружности – система на границе устойчивости. Если хотя бы один корень лежит вне круга – система неустойчива.

Рис. 1.40. Отображение р-плоскости в z-плоскость (а),

круг единичного радиуса комплексной плоскости z (б)

Соответствие p-плоскости, z-плоскости и временных характеристик при различных случаях корней характеристического уравнения изображено на рис. 1.41.

	р
	р
		р
	р

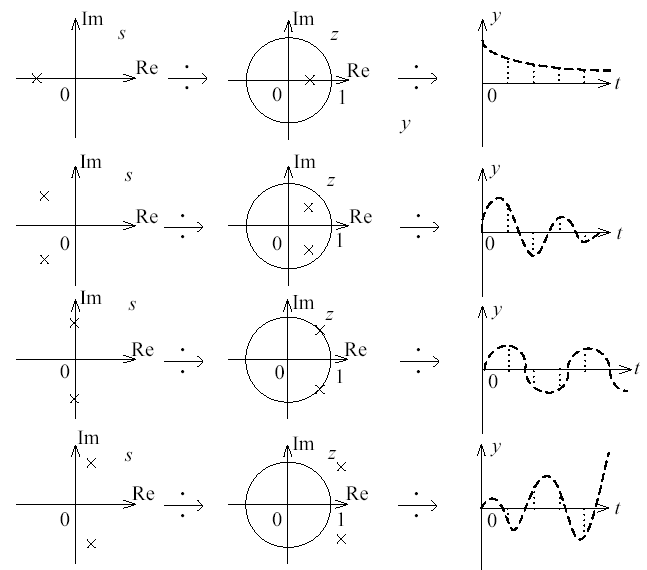
Рис. 1.41. Соответствие корней характеристического уравнения p-плоскости,

z-плоскости и временных характеристик

Пример. Оценить устойчивость импульсной системы со структурой, представленной на рис.1.42.

		р
	р

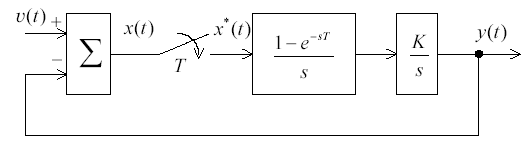Рис. 1.42. Структурная схема ИАСУ

Передаточная функция разомкнутой системы .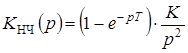

Перейдя к z-преобразованию, получим .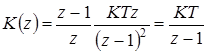

Передаточная функция замкнутой системы 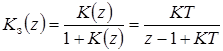, откуда характеристическое уравнение z + (KT – 1) = 0. Здесь единственный корень z = 1 – KT. По условию устойчивости 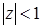, то есть ½1 – KT½<1 и окончательно область устойчивости будет иметь вид неравенства: 0<KT<2. При всех других значениях K и T импульсная система будет неустойчивой.

В дискретных, как и в непрерывных системах, используют критерии устойчивости, позволяющие судить об устойчивости без определения корней.

Их применение основано на формуле билинейного преобразования

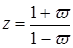, (1.57)

которое позволяет отобразить единичный круг плоскости z в левую часть комплексной плоскости w.

Такое преобразование называют также дробно-линейным преобразованием. Оно позволяет отобразить внутренности единичного круга в плоскости z на левую полуплоскость плоскости w, причем контур окружности единичного радиуса переходит при этом в мнимую ось на w-плоскости (рис. 1.43).

Рис. 1.43. К вопросу дробно-линейного преобразования

Пример. Характеристическое уравнение системы 1-го порядка

.

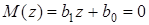Определить условия устойчивости системы.

Решение.

С учетом формулы билинейного преобразования 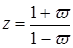, запишем исходное характеристическое уравнение в следующем виде

,

,

.

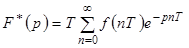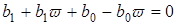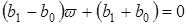Условие устойчивости

.

Пусть 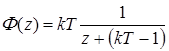, тогда

,

,

.

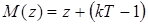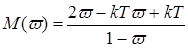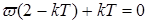Условие устойчивости

.

Здесь раскрывается важное свойство импульсных систем: устойчивость зависит как от общего коэффициента передачи k системы в разомкнутом состоянии, так и от периода дискретности T.

Для систем 2-го порядка необходимым и достаточным условием является положительность коэффициентов характеристического уравнения. Для систем 3-го и выше порядка применяют критерий Гурвица. Можно также применить критерий Михайлова.