Самостоятельная работа студентов (срс)
Самостоятельное изучение тем разделов программы (материалы для самостоятельной работы студентов: УМК дисциплины («Математика»).
5.1 Виды СРС
| Наименование СРС | Количество часов по семестрам |
| Выполнение курсового проекта | - |
| Выполнение курсовой работы | - |
| Выполнение РЗ | - |
| Написание реферата по разделу дисциплины | - |
| Написание реферата по дисциплине ООП | - |
| Выполнение контрольной работы | |
| Сдача коллоквиума | - |
| Самостоятельное изучение тем разделов программы Подготовка к практическим занятиям | |
| Итого: |
5.2 Примерный перечень домашних семестровых заданий для заочников
| Семестр | Кол-во КР | Кол-во часов | Тема |
| I | Элементы линейной и векторной алгебры. Элементы аналитической геометрии. Основы дифференциального исчисления функции одной и нескольких переменных. | ||
| II | Неопределенный и определенный интегралы. Кратные и криволинейные интегралы. Элементы теории поля. | ||
| III | Обыкновенные дифференциальные уравнения. Числовые и функциональные ряды. | ||
| IV | Теория вероятностей. Математическая статистика. Статистические методы обработки экспериментальных данных. | ||
| Итого: 160 часов |
5.3 Примерный перечень тем курсовых проектов (работ).
Курсовые работы не предусмотрены.
5.4 Примерный перечень тем рефератов.
Рефераты не предусмотрены.
5.5 Самостоятельное изучение тем разделов программы (материалы для самостоятельной работы студентов:УМК дисциплины «Математика»).
Виды СРС
| Наименование СРС | Количество часов по семестрам |
| Выполнение курсового проекта | - |
| Выполнение курсовой работы | - |
| Выполнение РЗ | - |
| Написание реферата по разделу дисциплины | - |
| Написание реферата по дисциплине ООП | - |
| Выполнение контрольной работы | |
| Сдача коллоквиума | - |
| Самостоятельное изучение тем разделов программы Подготовка к практическим, лабораторным занятиям | |
| Итого: |
6.Методические указания к самостоятельной работе студентов.
Векторный анализ
ВЕКТОРНОЕ ПОЛЕ. ВЕКТОРНЫЕ ЛИНИИ И ИХ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Определение 6.1.1. Векторным полем точки М называется векторная функция 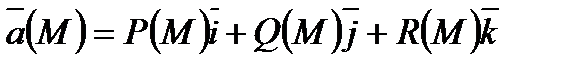 точки М вместе с областью ее определения.
точки М вместе с областью ее определения.
Задание векторного пространственного поля равносильно заданию трех скалярных функций 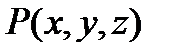 ,
, 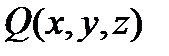 ,
, 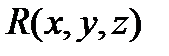 , являющихся проекциями вектора
, являющихся проекциями вектора 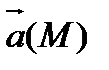 на координатные оси. Примерами векторных полей являются поле магнитной напряженности, поле сил тяготения, поле скоростей установившегося потока жидкостей и т.д.
на координатные оси. Примерами векторных полей являются поле магнитной напряженности, поле сил тяготения, поле скоростей установившегося потока жидкостей и т.д.
Определение 6.1.2. Векторной линией поля 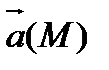 называется такая линия, в каждой точке которой касательная совпадает с направлением вектора
называется такая линия, в каждой точке которой касательная совпадает с направлением вектора 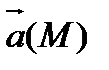 . Векторная линия обычно называется линией тока для поля скоростей, силовой линией – для силового поля.
. Векторная линия обычно называется линией тока для поля скоростей, силовой линией – для силового поля.
Как известно, направляющие косинусы касательной пропорциональны дифференциалам 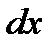 ,
, 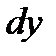 ,
, 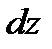 . Для нахождения векторных линий поля
. Для нахождения векторных линий поля 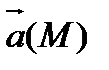 векторов
векторов 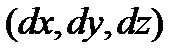 и
и 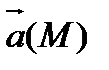
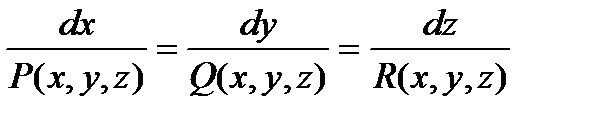
 , (6.1.1)
, (6.1.1)
где 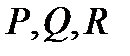 - проекция вектора
- проекция вектора 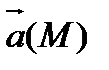 на координатные оси.
на координатные оси.
Уравнения (6.1.1.) называются дифференциальными уравнениями векторных линий поля 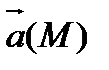 . Если
. Если 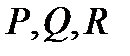 - непрерывно дифференцируемые функции и в точке М вектор
- непрерывно дифференцируемые функции и в точке М вектор 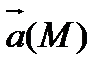 отличен от нуля, то через точку М проходит одна определенная векторная линия поля
отличен от нуля, то через точку М проходит одна определенная векторная линия поля 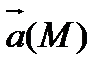 .
.
Пример 6.1.1. Найти векторные линии поля 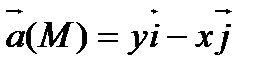 .
.
Решение. Дифференциальные уравнения векторных линий имеют вид 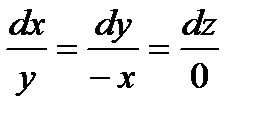 или
или 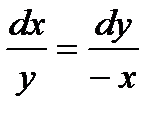 ,
, 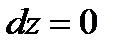 ;
;
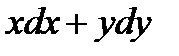 ,
, 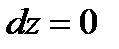 . Интегрируя, получим
. Интегрируя, получим 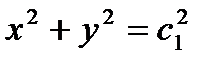 и
и 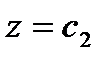 , где
, где 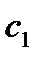 и
и 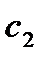 - произвольные постоянные. Векторными линиями являются окружности, расположенные в плоскостях, параллельных плоскости
- произвольные постоянные. Векторными линиями являются окружности, расположенные в плоскостях, параллельных плоскости 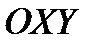 и в самой плоскости
и в самой плоскости 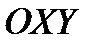 при
при 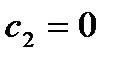 .
.
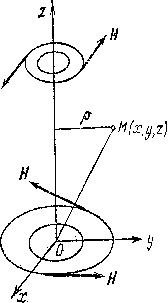
Пример 6.1.2. Найти векторные линии магнитного поля бесконечного проводника тока.
Решение. Будем считать, что проводник направлен по оси 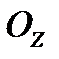 и в этом же направлении течет ток I . Вектор напряженности H магнитного поля, создаваемого током, равен
и в этом же направлении течет ток I . Вектор напряженности H магнитного поля, создаваемого током, равен
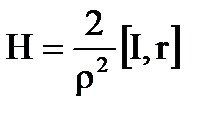 , (6.1.2)
, (6.1.2)
где 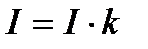 есть вектор тока,
есть вектор тока, 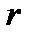 - радиус-вектор точки
- радиус-вектор точки 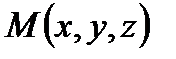 ,
, 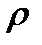 - расстояние от оси провода до точки М. Раскрывая векторное произведение (6.1.2), получим
- расстояние от оси провода до точки М. Раскрывая векторное произведение (6.1.2), получим
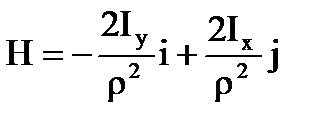 .
.
Дифференциальные уравнения векторных линий:
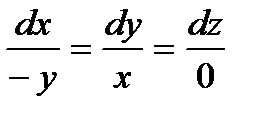 ,
,
откуда
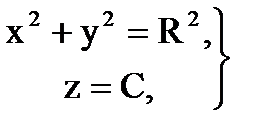 ,
,
т.е. векторные линии являются окружностями с центрами на оси 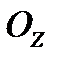
ПОТОК ВЕКТОРНОГО ПОЛЯ ЧЕРЕЗ ПОВЕРХНОСТЬ
Определение 6.1.3. Потоком П векторного поля 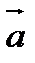 через
через
двустороннюю поверхность 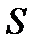 называется поверхностный интеграл
называется поверхностный интеграл
второго рода.
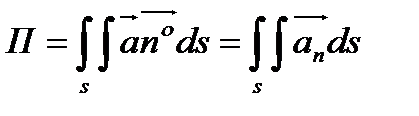 , (6.1.3)
, (6.1.3)
где 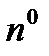 - единичный вектор нормали к
- единичный вектор нормали к 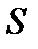 , указывающей её ориентацию;
, указывающей её ориентацию; 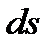 - элемент площади поверхности
- элемент площади поверхности 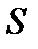 ;
; 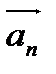 - проекция вектора
- проекция вектора 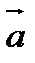 на направление
на направление 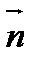 .
.
Дадим физическое истолкование формулы (6.1.2). Пусть 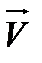 - скорость жидкости, протекающей через произвольную (двустороннюю) поверхность
- скорость жидкости, протекающей через произвольную (двустороннюю) поверхность 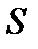 . Рассмотрим разбиение
. Рассмотрим разбиение 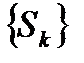 поверхности на n частей
поверхности на n частей 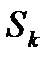 с площадками
с площадками 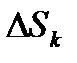 . Тогда произведение
. Тогда произведение 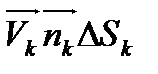 равно количеству жидкости, протекающей через поверхность
равно количеству жидкости, протекающей через поверхность 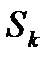 за единицу времени в
за единицу времени в
направлении вектора  .
.
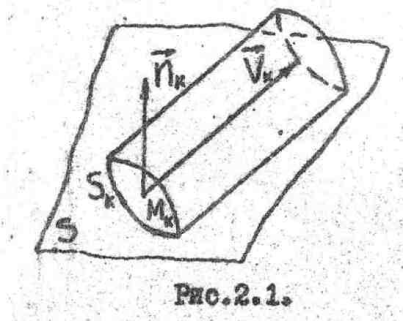
Интеграл 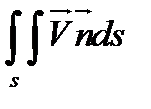 , являющийся
, являющийся
пределом интегральной суммы
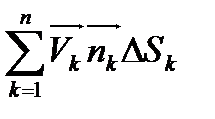 , дает полное количество жидкости, протекающей в единицу времени через
, дает полное количество жидкости, протекающей в единицу времени через 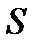 в положительном направлении. Пусть
в положительном направлении. Пусть 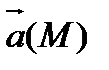 - поле скоростей в стационарном течении жидкости, так что ее скорость
- поле скоростей в стационарном течении жидкости, так что ее скорость 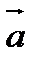 в точке М зависит лишь от М, но не зависит от времени. Из сказанного выше следует, что поток скорости через ориентированную поверхность
в точке М зависит лишь от М, но не зависит от времени. Из сказанного выше следует, что поток скорости через ориентированную поверхность 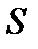 за единицу времени в том направлении, в котором ориентирована эта поверхность (физический смысл потока).
за единицу времени в том направлении, в котором ориентирована эта поверхность (физический смысл потока). Вычисление потока
Вычисление методом проектирования на одну
из координатных плоскостей
Пусть поверхность 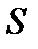 задана уравнением
задана уравнением 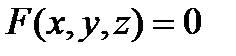 .Единичный вектор нормали
.Единичный вектор нормали 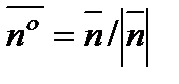 , но, как известно,
, но, как известно, 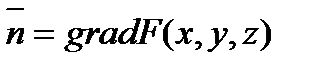
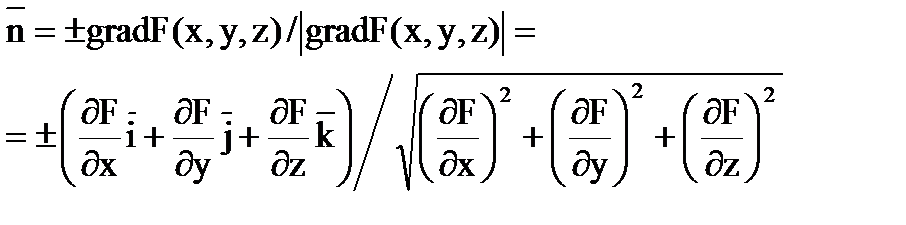 .
.
Знак в правой части берется так, чтобы получить нормальный вектор 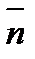 именно к выбранной стороне поверхности.
именно к выбранной стороне поверхности.
Если поверхность задана уравнением 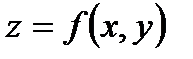 , то
, то 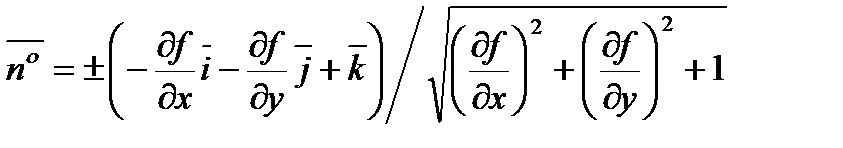 .
.
Знак «+» соответствует выбору верхней стороны поверхности, нормаль к которой образует острый угол с осью 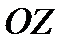 и, следовательно, направляющий косинус положителен.
и, следовательно, направляющий косинус положителен.
Известно также, что 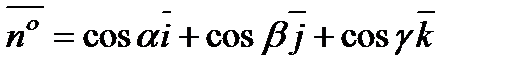 и
и 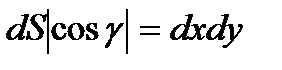 .
.
Пусть поверхность 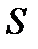 взаимно однозначно проектируется на плоскость
взаимно однозначно проектируется на плоскость 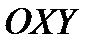 в область
в область 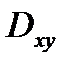 , тогда вычисление потока векторного поля через поверхность
, тогда вычисление потока векторного поля через поверхность 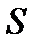 сводится к вычислению двойного интеграла
сводится к вычислению двойного интеграла
по области 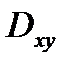 :
: 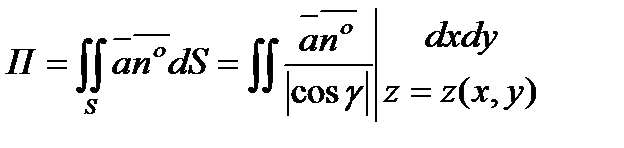 . (6.1.4.)
. (6.1.4.)
Аналогично, если поверхность 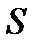 взаимно однозначно проектируется на плоскость
взаимно однозначно проектируется на плоскость 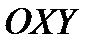 или
или 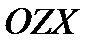 , то поток вычисляется по формулам
, то поток вычисляется по формулам 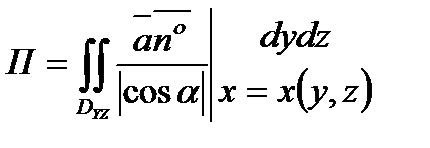 ;
; 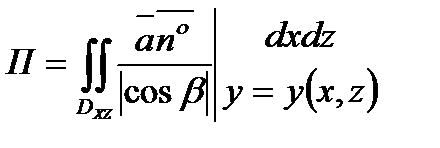 .
.
Пример 6.1.3. Найти поток векторного поля 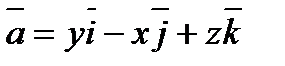 через поверхность конуса
через поверхность конуса 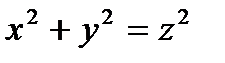 и плоскость
и плоскость 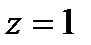 .
.
Решение. Обозначим потоки векторного поля: 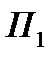 через боковую поверхность конуса
через боковую поверхность конуса 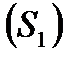 и
и 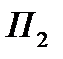 через плоскость
через плоскость 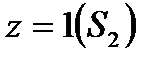 .
.
Тогда весь поток П=П1 +П2 =
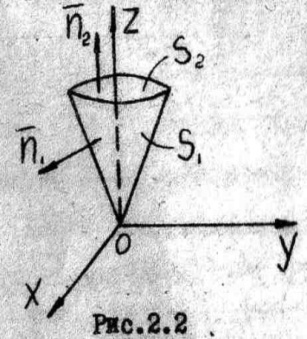
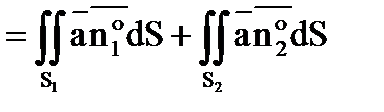 .
.
Вычислим 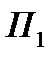 . Уравнение
. Уравнение 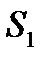 :
:
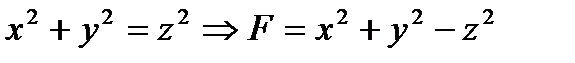 .
. Проекция вектора 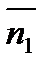 на ось
на ось 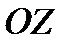 отрицательна.
отрицательна.
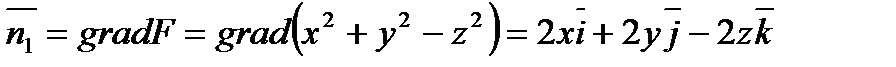 ;
;
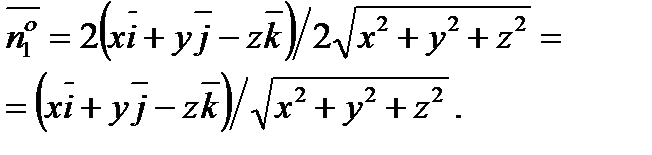
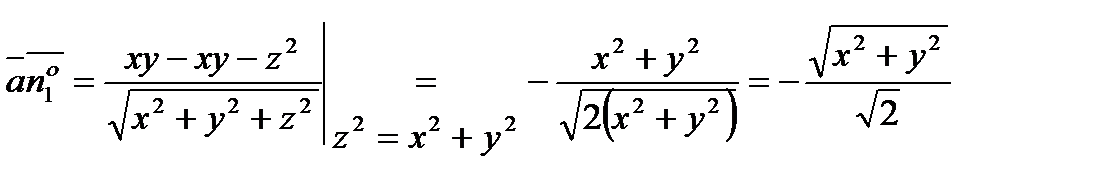 .
.
Из выражения для (6.1.3.) найдем
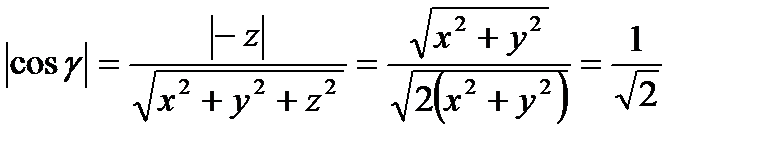 .
.
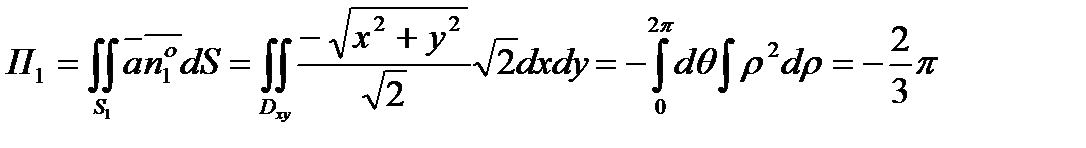 .
.
Вычислим 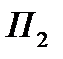 . Уравнения поверхности
. Уравнения поверхности 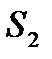 :
: 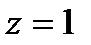 ,
, 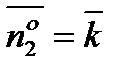 ,
, 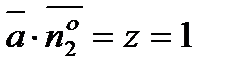 (На поверхности
(На поверхности 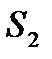 ),
),
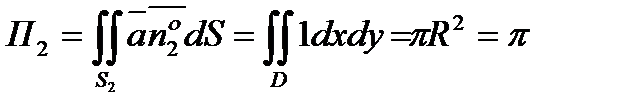 .
.
Следовательно, 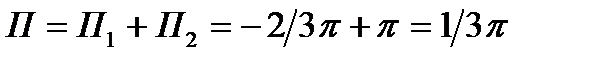 .
.
Пример 6.1.4. Найти поток векторного поля 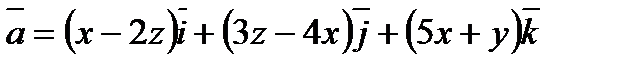 через верхнюю сторону треугольника с вершинами в точках
через верхнюю сторону треугольника с вершинами в точках 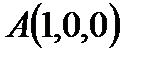 ,
, 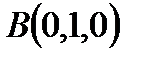 ,
, 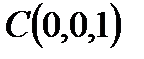 .
.
Решение. Уравнение плоскости 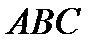 составим как уравнение
составим как уравнение
 плоскости, проходящей через три точки
плоскости, проходящей через три точки
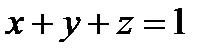 . Следовательно,
. Следовательно, 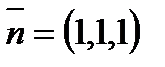 ,
,
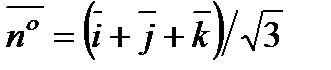 .
.
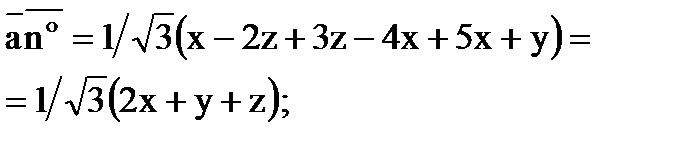
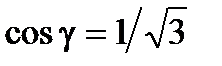 .
.
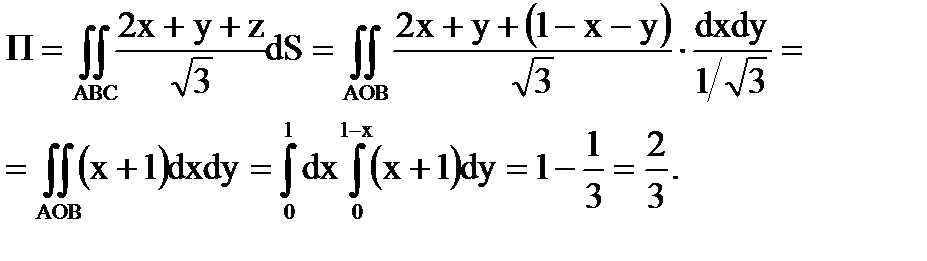
Пример 6. 1.5. Вычислить поток векторного поля
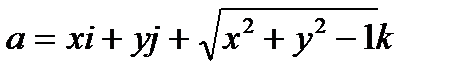
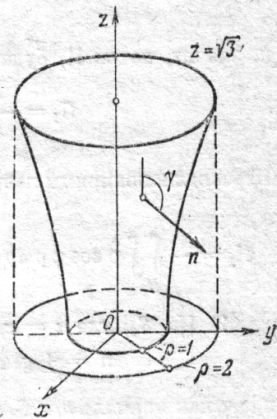 через внешнюю сторону однополостного гиперболоида
через внешнюю сторону однополостного гиперболоида 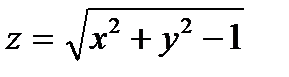 ,ограниченного плоскостями
,ограниченного плоскостями 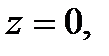
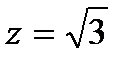 .
.
Решение. Данная поверхность проектируется взаимно однозначно на плоскость 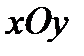 в область
в область 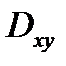 , ограниченную окружностями
, ограниченную окружностями
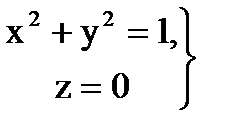 и
и 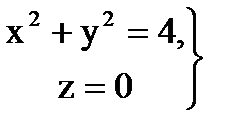 .
.
Находим внешнюю нормаль 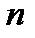 : рис.6.1.5.
: рис.6.1.5. 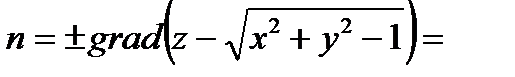
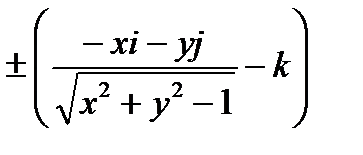 .
.
Т.к. 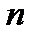 образует с осью
образует с осью 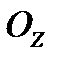 тупой угол
тупой угол 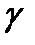 , то берем знак минус и, значит,
, то берем знак минус и, значит, 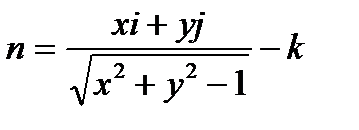 .
.
Находим скалярное произведение 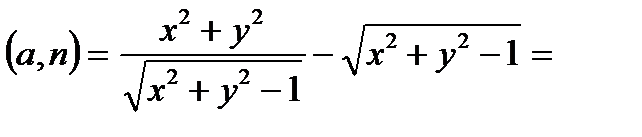
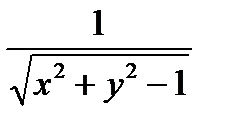 .
.
Применяя формулу
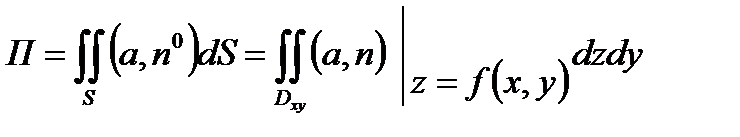 ,
,
получим 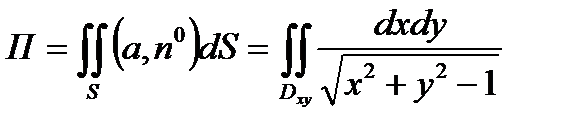 .
.
Переходя к полярным координатам 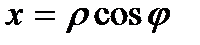 ,
, 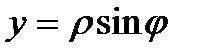 , будем иметь
, будем иметь 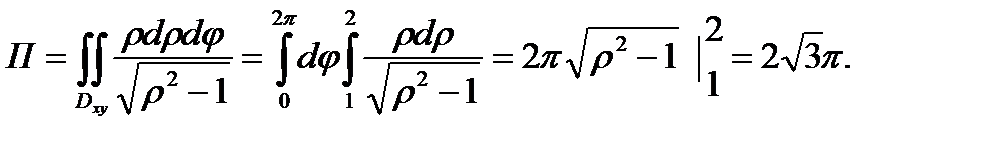
Вычисление потока методом проектирования
на все три координатные плоскости
Пусть поверхность 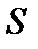 взаимно однозначно проектируется на все три координатные плоскости:
взаимно однозначно проектируется на все три координатные плоскости:
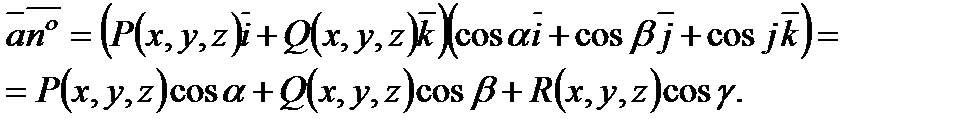
Тогда поток векторного поля 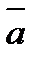 равен
равен
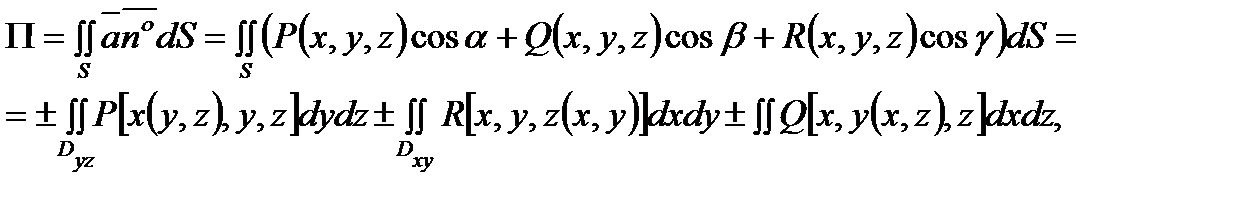
где знак перед каждым из двойных интегралом берется соответственно таким, каков знак 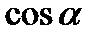 ,
, 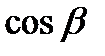 ,
, 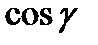 на поверхности
на поверхности 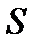 .
.
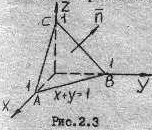
Пример 6.1.6. Найти поток векторного поля 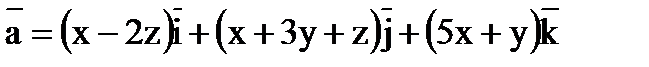 через треугольник, получаемый при пересечении плоскости
через треугольник, получаемый при пересечении плоскости 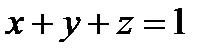 с координатными плоскостями (выбор указан на рис. 6.1.6,).
с координатными плоскостями (выбор указан на рис. 6.1.6,).
Решение. Найдем 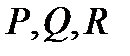 . P[x(y,z),y,z]=(1-y-z)-2z=1-y-3z (выразили из уравнения плоскости)
. P[x(y,z),y,z]=(1-y-z)-2z=1-y-3z (выразили из уравнения плоскости)
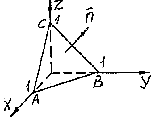
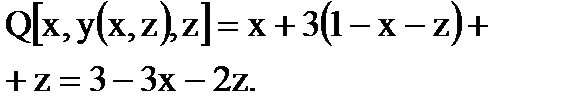
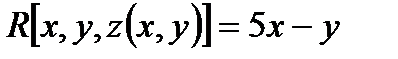 .
.
По формуле (6.1.3) получим
Рис. 6.1.6
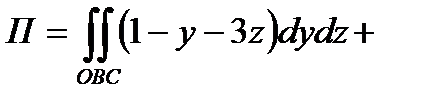
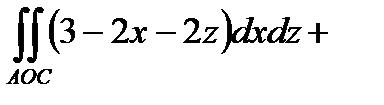
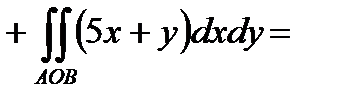
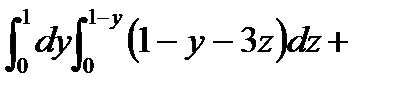
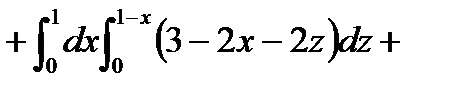
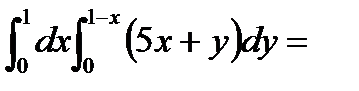
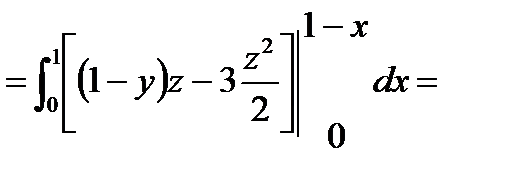
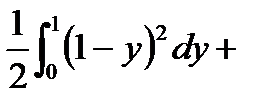
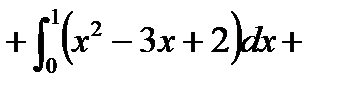
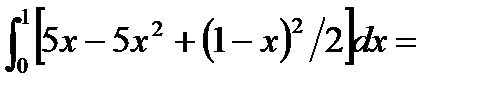
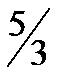 .
.
При вычислении потока векторного поля через боковую поверхность кругового цилиндра или через сферу удобно пользоваться соответственно цилиндрическими или сферическими координатами.
Пример 6.1.7. Найти поток векторного поля
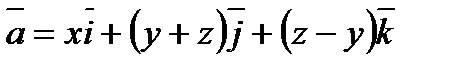 через часть сферической поверхности
через часть сферической поверхности 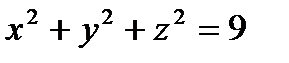 , расположенную в первом октанте.
, расположенную в первом октанте.
Решение. Найдем вектор- градиент 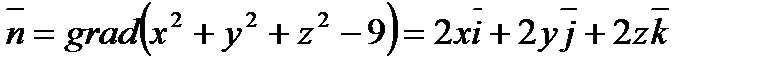 ,
,
тогда единичный вектор 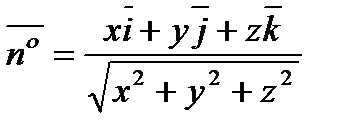 ;
; 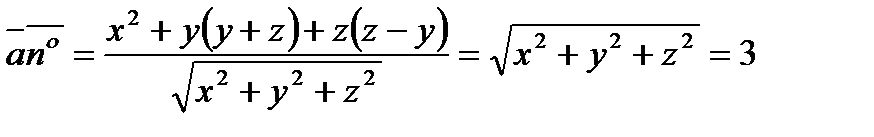 .
.
По условию задачи поверхность находится в первом октанте, т.е. 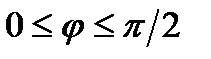 ,
, 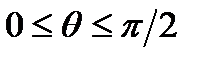 , элемент площади в сферических координатах равен
, элемент площади в сферических координатах равен 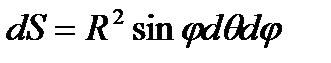 . Следовательно, поток через часть сферы вычисляется по формуле
. Следовательно, поток через часть сферы вычисляется по формуле 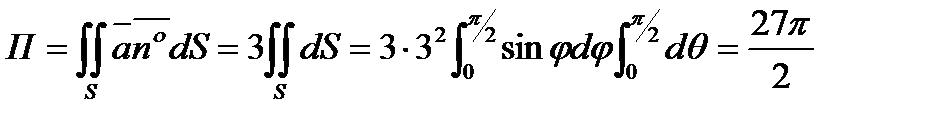 .
.
Вычисление потока методом введения
криволинейных координат на поверхности
В некоторых случаях при вычислении потока векторного поля через данную поверхность S возможно выбрать на самой поверхности простую систему координат, в которой удобно вычислять поток, не применяя проектирования на координатные плоскости.
Рассмотрим частные случаи.
Случай 1). Пусть поверхность S является частью кругового цилиндра 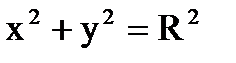 , ограниченного поверхностями
, ограниченного поверхностями 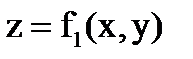 и
и 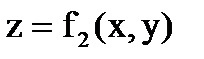 .
.
Полагая 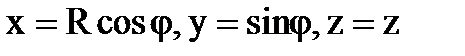 , будем иметь для данной поверхности
, будем иметь для данной поверхности 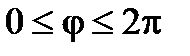 ,
,
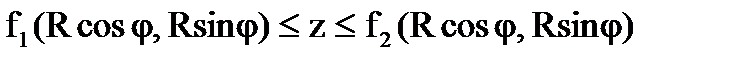 , а для элемента площади dS получаем следующее выражение (рис.6. 1.8.):
, а для элемента площади dS получаем следующее выражение (рис.6. 1.8.):
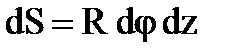 .
.
Тогда поток векторного поля a
через внешнюю сторону поверхности S
вычисляется по формуле
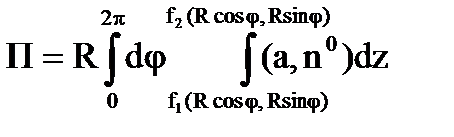 , (6.1.5)
, (6.1.5)
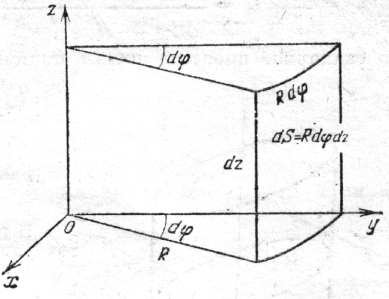 где
где
Рис.6.1.7.
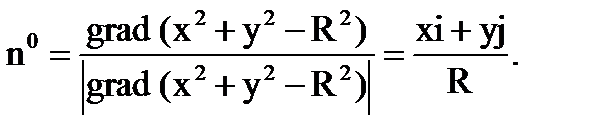
Пример 6. 1.8. Вычислить поток радиуса-вектора
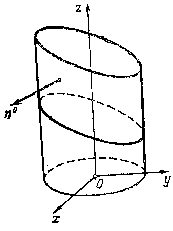
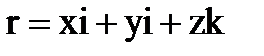 через боковую поверхность кругового цилиндра
через боковую поверхность кругового цилиндра 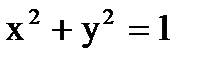 , ограниченного снизу плоскостью
, ограниченного снизу плоскостью 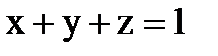 , а сверху – плоскостью
, а сверху – плоскостью 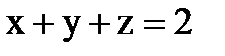 .
.
Решение. В данном случае (рис. 6.1.7) имеем
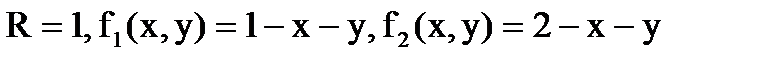 .
.
Переходя к координатам на цилиндре
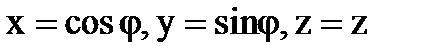 будем рис.6.1.8
будем рис.6.1.8
иметь 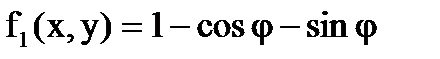 ,
,
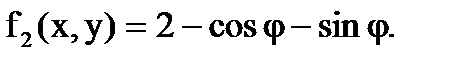
Согласно формуле (6.1.4) поток вектора r
будет равен
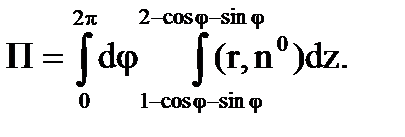
Но так как на цилиндре 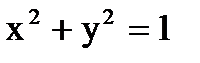
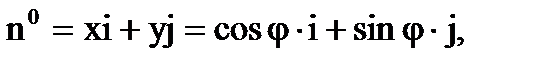
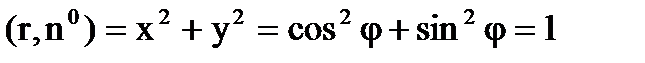
и, следовательно,
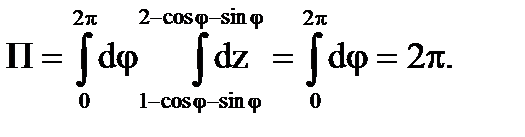
Случай 2). Пусть поверхность S является частью сферы 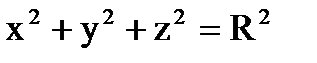 , ограниченной коническими поверхностями, уравнения которых в сферических координатах имеют вид
, ограниченной коническими поверхностями, уравнения которых в сферических координатах имеют вид 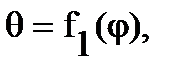 и полуплоскостями
и полуплоскостями 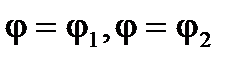 .
.
Положим для точек данной сферы
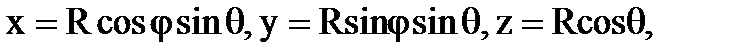
где 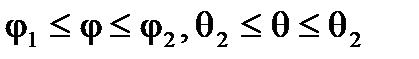 .
.
Тогда для элемента площади dS полу- чим (рис. 6.1.8)
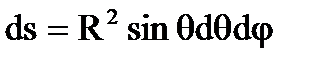 .
.
В этом случае поток векторного поля а через внешнюю часть S сферы вычисляется по формуле
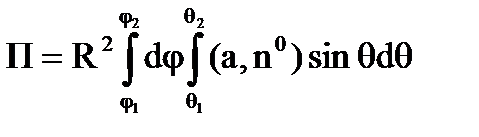 ( 6.1.6)
( 6.1.6)
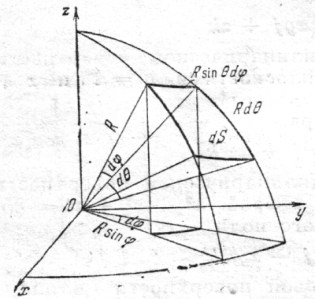
Рис.6.1.9.
где
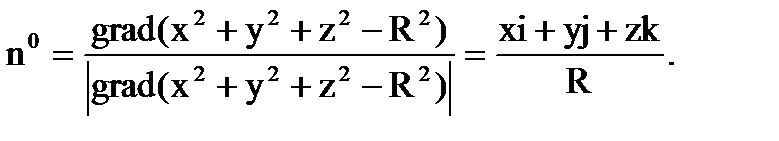
Пример 6.1.9. Найти поток вектора
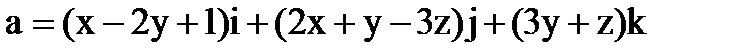
через часть поверхности сферы 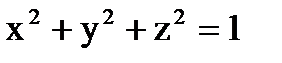 , расположенную в первом октанте, в область, где
, расположенную в первом октанте, в область, где 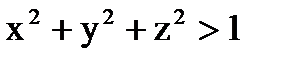 .
.
Решение. В данном случае имеем
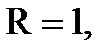
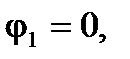
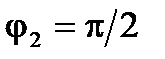 ,
, 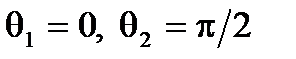 ,
,
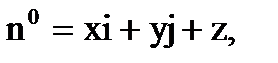
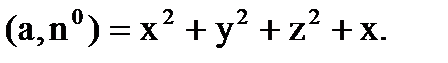
Введем на сфере 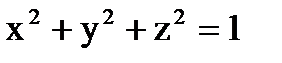 координаты
координаты 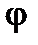 и
и 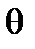 так, что
так, что

Тогда будет иметь 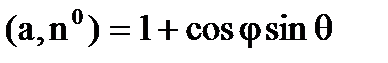
и, применяя формулу (6.1.5), получим
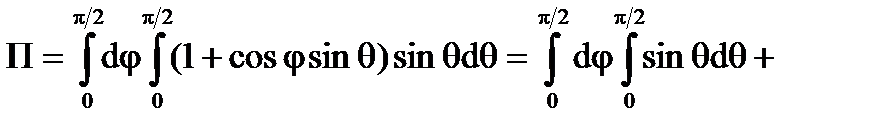
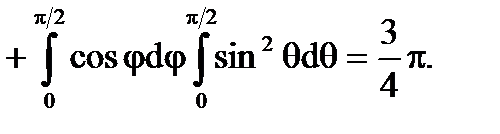
ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ.
ФОРМУЛА ОСТРОГРАДСКОГО
Вычисление дивергенции
Определение 6.1.4. Отношение потока векторного поля через поверхность 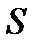 к величине объема
к величине объема 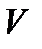 называется средней объемной плотностью потока векторного поля.
называется средней объемной плотностью потока векторного поля.
В поле скоростей жидкости это отношение при 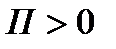 определяет среднее количество жидкости, поступающей из единицы объема внутри поверхности
определяет среднее количество жидкости, поступающей из единицы объема внутри поверхности 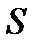 за единицу времени. При
за единицу времени. При 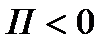 определяет среднее количество жидкости, поглощаемой единицей объема за единицу времени.
определяет среднее количество жидкости, поглощаемой единицей объема за единицу времени.
Определение 6. 1.5. Дивергенцией (или расходимостью) векторного поля 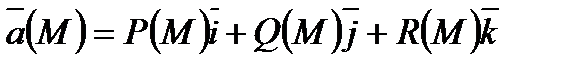 называется объемная
называется объемная
плотность потока векторного поля 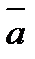 в этой точке:
в этой точке:
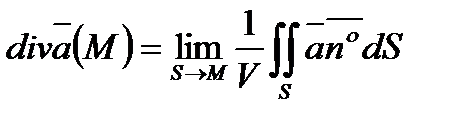 ,
,
где V-объем, ограниченный замкнутой поверхностью 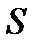 , содержащей точку М.
, содержащей точку М.
Если координаты вектора 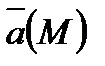 непрерывны вместе со своими частными производными
непрерывны вместе со своими частными производными 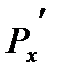 ,
, 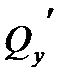 ,
, 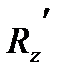 , то в декартовой системе координат дивергенция вычисляется по формуле
, то в декартовой системе координат дивергенция вычисляется по формуле
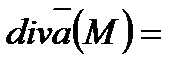
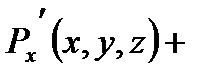
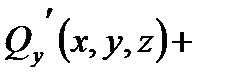
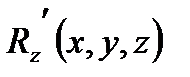 , (6.1.7)
, (6.1.7)
где частные производные вычислены в точке М.
Пример 6.1.10. Вычислить дивергенцию поля радиус-вектора 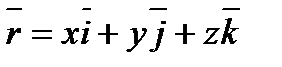 .
.
Решение.
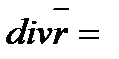
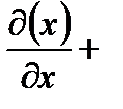
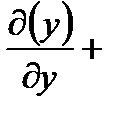
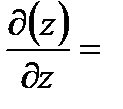
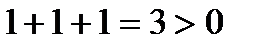 .
.
Следовательно, в каждой точке поля радиус-вектора имеется источник, плотность которого равна трем единицам.
Формула Остроградского в векторной форме
Равенство (6.1.6.) позволяет записать формулу Остроградского в векторной форме. Если учесть, что

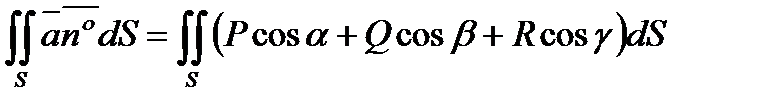 (6.1.8.)
(6.1.8.)
является потоком векторного поля, тогда равенство
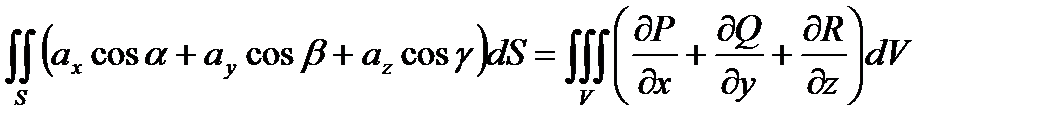 примет следующий вид:
примет следующий вид:
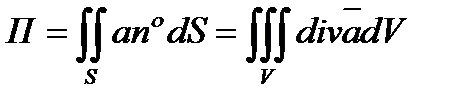 . (6.1.9.)
. (6.1.9.)
Физический смысл формулы Остроградского заключается в том, что, если 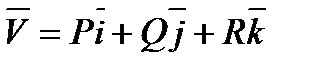 - вектор скорости жидкости, протекающей через тело
- вектор скорости жидкости, протекающей через тело 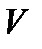 ,тогда подынтегральное выражение в правой части равенства (6.1.8.) дает полное количество жидкости ,вытекающей из тела
,тогда подынтегральное выражение в правой части равенства (6.1.8.) дает полное количество жидкости ,вытекающей из тела 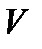 или через поверхность
или через поверхность 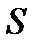 за единицу времени (или втекающей в тело
за единицу времени (или втекающей в тело 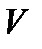 , если интеграл отрицателен) .Если дивергенция равна нулю , то количество жидкости , втекающей внутрь тела , равно количеству жидкости , вытекающей из него .
, если интеграл отрицателен) .Если дивергенция равна нулю , то количество жидкости , втекающей внутрь тела , равно количеству жидкости , вытекающей из него .
Формула (6.1.9.) позволяет упростить вычисления потоков через замкнутую поверхность.
Пример 6.1.11. Вычислить поток поля 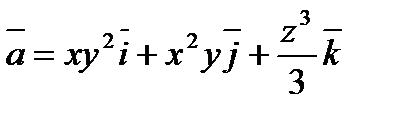 через полную поверхность цилиндра
через полную поверхность цилиндра
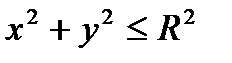 ,
, 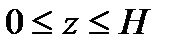 .
.
Решение. Найдем дивергенцию
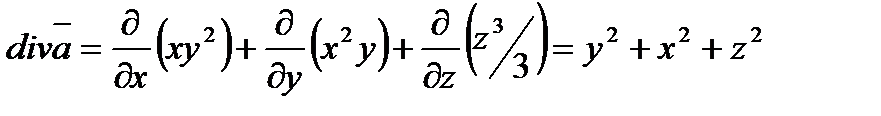 .
.
По формуле (6.1.9.)
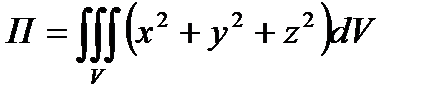 .
.
Перейдем к циклическим координатам, тогда 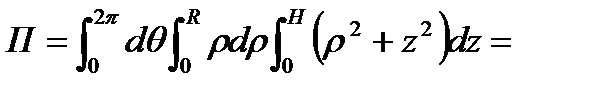
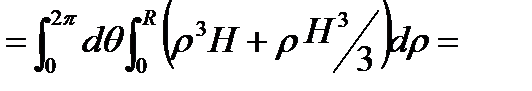
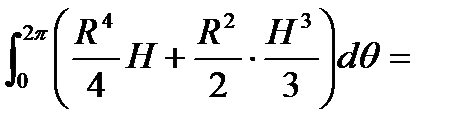
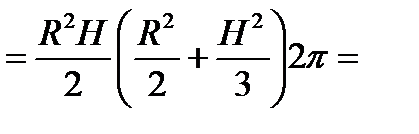
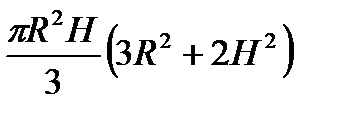 .
.
ЛИНЕЙНЫЙ ИНТЕГРАЛ В ВЕКТОРНОМ ПОЛЕ.
ЦИРКУЛЯЦИЯ. ПЛОТНОСТЬ ЦИРКУЛЯЦИИ
Определение и вычисление циркуляции
Пусть L-пространственная кусочно-гладкая направленная линия и 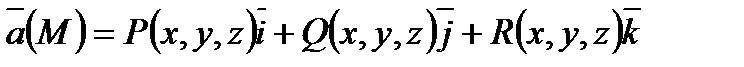 - непрерывное векторное поле, заданное в
- непрерывное векторное поле, заданное в 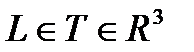 , где
, где 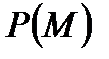 ,
, 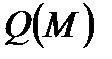 ,
, 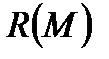 - проекции
- проекции 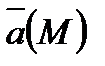 на координатные оси.
на координатные оси.
Определение 6.1.6. Криволинейный интеграл вида
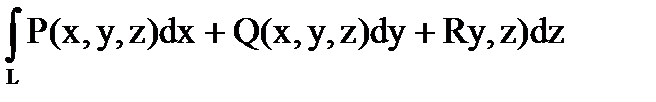 ,
,
взятый по некоторой направленной линии L, называется линейным интегралом от вектора 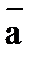 вдоль линии L.
вдоль линии L.
Пример 6. 1.12. Вычислить работу силового поля
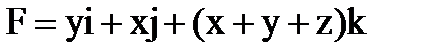 вдоль отрезка AB прямой, проходящей через точки M1(2,3,4) и M2(3,4,5).
вдоль отрезка AB прямой, проходящей через точки M1(2,3,4) и M2(3,4,5).
Решение. Работа данного силового поля будет равна линейному интегралу вдоль отрезка M1M2:
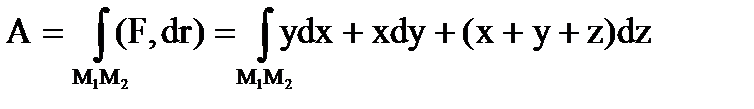 .
.
Находим канонические уравнения прямой M1M2. Имеем
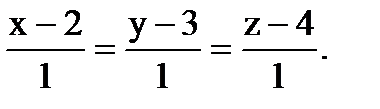
Отсюда 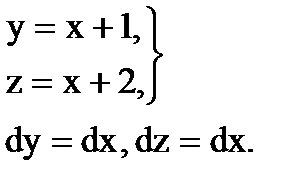
Здесь x изменяется в пределах от 2 до 3 (так как абсцисса точки M1 равна 2, а абсцисса точки M2 равна 3). Искомая работа будет равна
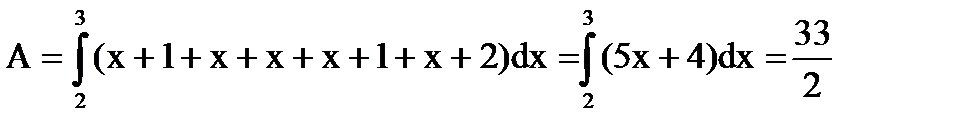 .
.
Определение 6.1.7. Циркуляцией векторного поля 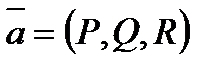 по замкнутой линии L в области
по замкнутой линии L в области 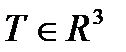 называется линейный интеграл по этой замкнутой линии L, обозначаемый через Ц и определяемый формулой
называется линейный интеграл по этой замкнутой линии L, обозначаемый через Ц и определяемый формулой 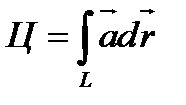 , где
, где 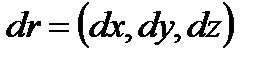 - вектор-дифференциал.
- вектор-дифференциал.
В том случае, когда 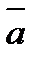 - силовое поле, линейный интеграл от вектора
- силовое поле, линейный интеграл от вектора 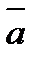 равен работе сил поля при перемещении тока по линии L(физический смысл циркуляции).
равен работе сил поля при перемещении тока по линии L(физический смысл циркуляции).
Найдем скалярное произведение векторов 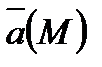 и
и 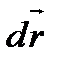 . Вектор
. Вектор 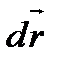 направлен по касательной к кривой L .
направлен по касательной к кривой L .
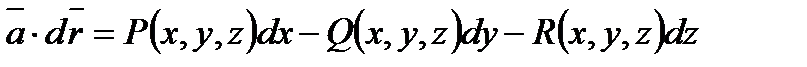 .
.
Тогда циркуляция принимает вид
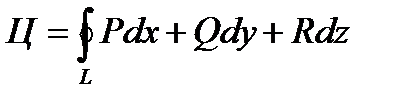 .
.
Пример 6.1.13. Найти циркуляцию векторного поля 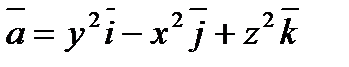 по контуру АВСА, полученному при пересечении параболоида
по контуру АВСА, полученному при пересечении параболоида 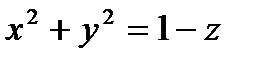 с координатными плоскостями
с координатными плоскостями
(рис.6. 1.9.).
Решение. 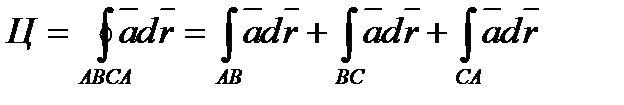 .
.
1. На АВ: 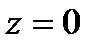 ,
, 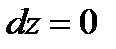 ;
; 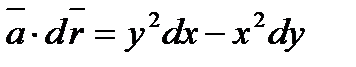 .
.
Линейный интеграл
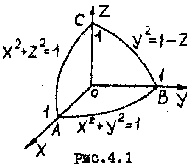
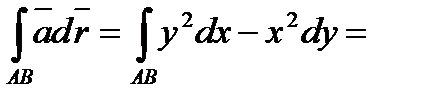
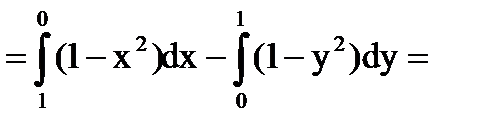
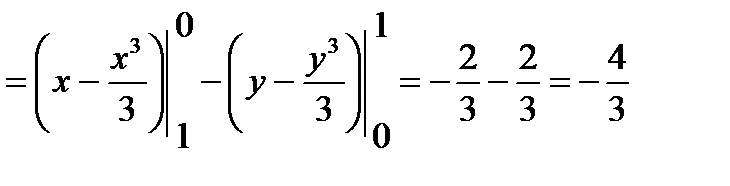 .
.
2. На ВС:  ,
, 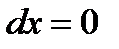 ,
, 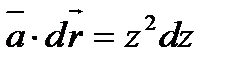
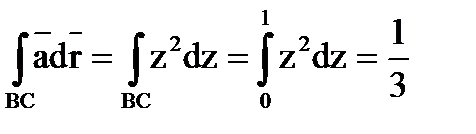 .
.
3. На СА: 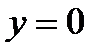 ,
, 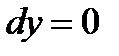 ;
; 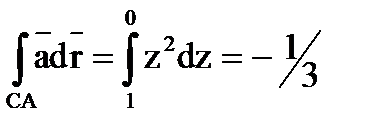 .
.
Таким образом, 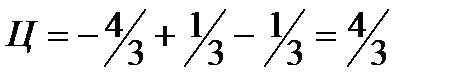 .
.
Знак минус указывает на то, что под действием сил поля 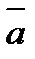 контур будет вращаться в отрицательном направлении, т.е. по часовой стрелке.
контур будет вращаться в отрицательном направлении, т.е. по часовой стрелке.
Пример 6.1.14. Вычислить циркуляцию векторного поля
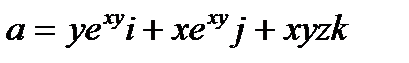 вдоль линии
вдоль линии 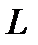 , получаемой пересечением конуса
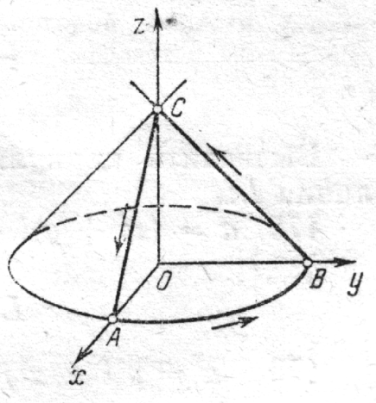
, получаемой пересечением конуса 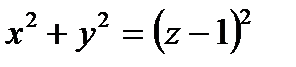 с координатными плоскостями (рис. 6.1.10).
с координатными плоскостями (рис. 6.1.10).
Решение. Линия 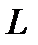 состоит из двух отрезков ВС и СА, расположенных на координатных плоскостях
состоит из двух отрезков ВС и СА, расположенных на координатных плоскостях 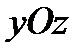 и
и 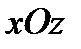 соответственно и
соответственно и
 дуги
дуги 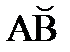 окружности
окружности
Рис. 6.1.10.
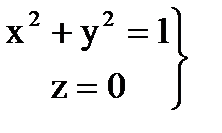 .
.
Поэтому циркуляция данного векторного поля будет равна
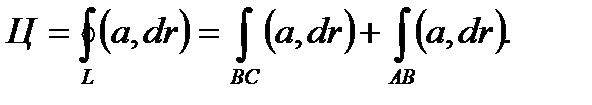
1. На отрезке ВС имеем 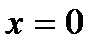 ,
,
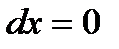 ;
; 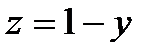 ,
, 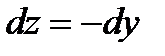 ;
;
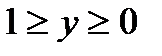 .
.
Следовательно, 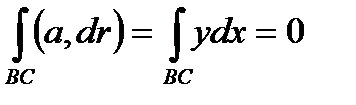 .
.
2. На отрезке СА имеем 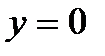 ,
, 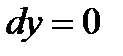 ;
; 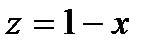 ,
, 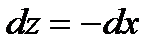 ;
; 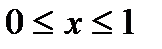 .
.
Следовательно, 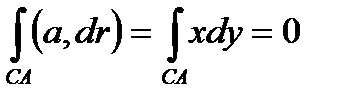 .
.
3. На дуге 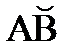 окружности
окружности 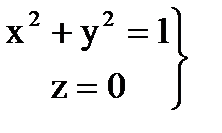 имеем
имеем 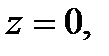
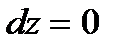 , и значит,
, и значит, 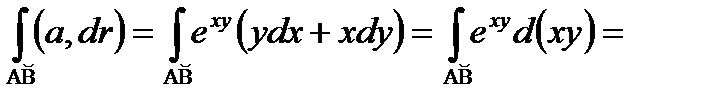
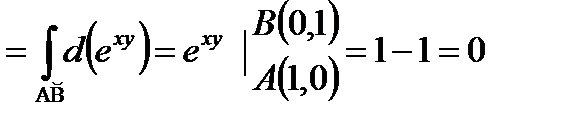 .
.
Искомая циркуляция векторного поля равна нулю.
Плотность циркуляции векторного поля
Пусть в векторном поле 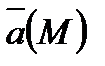 на поверхности
на поверхности 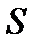 дан замкнутый контур L, заключающий в себе точку М
дан замкнутый контур L, заключающий в себе точку М
(рис. 6.1.11.)
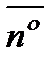 - единичный вектор нормали к
- единичный вектор нормали к
поверхности 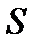 в т. М;
в т. М;
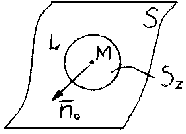
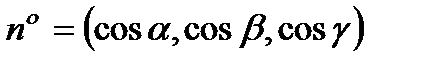 .
.
Пусть 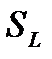 - площадь поверхности,
- площадь поверхности,
ограниченной контуром L.
Рис. 6.1.11.
Определение 6.1.8. Плотностью циркуляции в точке М называется предел отношения циркуляции к площади поверхности 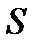 при условии стягивания контура
при условии стягивания контура 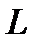 к точке М.
к точке М.
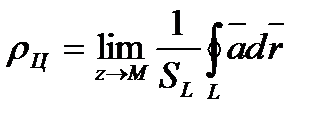 . (6.1.10)
. (6.1.10)
В проекциях плотность циркуляции выражается в виде 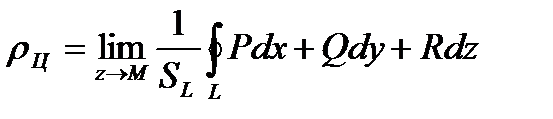 .
.
Если подынтегральное выражение преобразовать по формуле Стокса, то получим
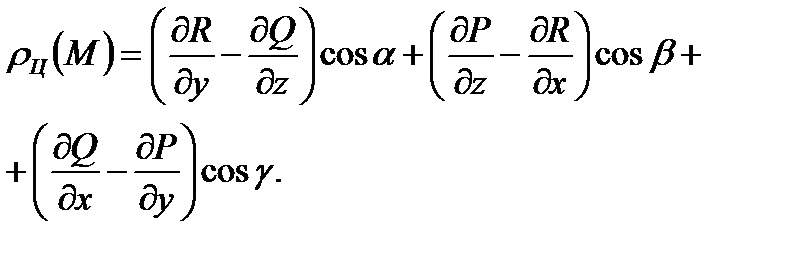 (6.1.11)
(6.1.11)
Частные производные вычислены в данной точке М.
РОТОР ВЕКТОРНОГО ПОЛЯ. ТЕОРЕМА СТОКСА
В ВЕКТОРНОЙ ФОРМЕ
Определение 6.1.9. Ротор (или вихрь) векторного поля точки М обозначается 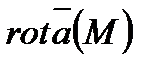 и определяется формулой
и определяется формулой 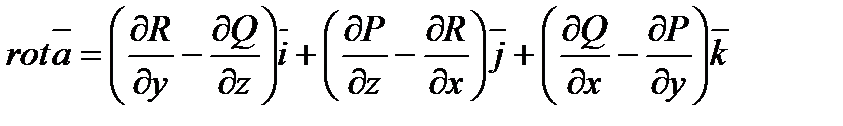 , (6.1.12)
, (6.1.12)
где частные производные вычислены в точке М.
Для лучшего запоминания этот вектор можно записать в виде следующего символического определителя:
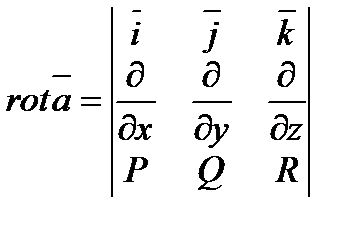 (6.1.13.)
(6.1.13.)
Смысловое определение ротора вытекает из его связи с плотностью циркуляции поля; сравнивая формулы (6.1.10.) и (6.1.11.), можно записать
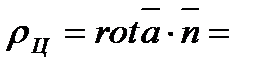
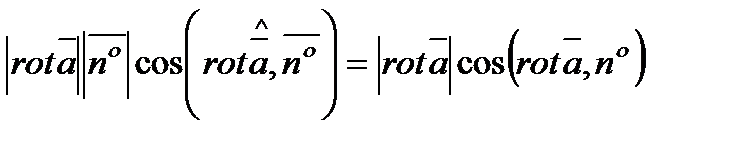 .
.
Если значение косинуса равно 1, то из последнего равенство 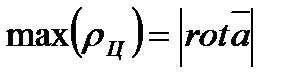 . Таким образом, плотность циркуляции в точке М будет наибольшей в направлении ротора и равна его численному значению. Физический смысл ротора в поле скоростей
. Таким образом, плотность циркуляции в точке М будет наибольшей в направлении ротора и равна его численному значению. Физический смысл ротора в поле скоростей 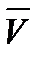 заключается в том, что ротор представляет собой мгновенную угловую скорость вращения тела.
заключается в том, что ротор представляет собой мгновенную угловую скорость вращения тела.
Пример 6.1.15. Найти ротор векторного поля 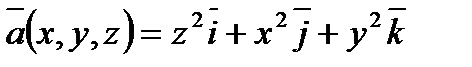 .
.
Решение. Используя формулу (6.1.12), найдем проекции ротора
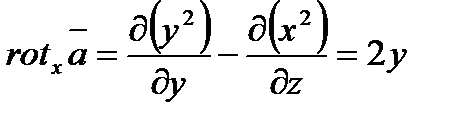 ;
; 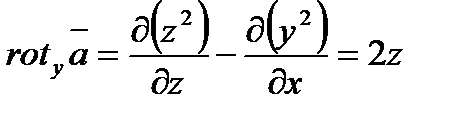 ;
;
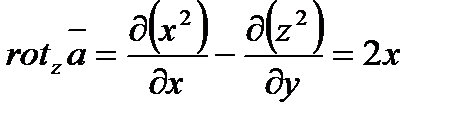 .
.
Следовательно, 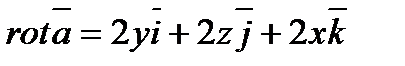 .
.
С помощью введенного 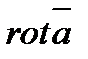 можно записать формулу Стокса в векторной форме. Так как
можно записать формулу Стокса в векторной форме. Так как 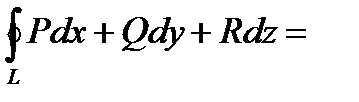
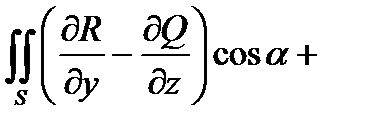
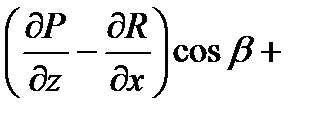 +
+ 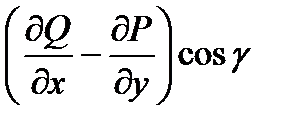 ,
,
следовательно, в векторной форме это равенство имеет вид 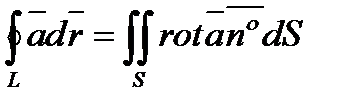 . (6.1.14) Итак, поток вектора
. (6.1.14) Итак, поток вектора 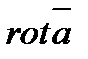 через ориентированную поверхность
через ориентированную поверхность 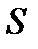 равен циркуляции вектора
равен циркуляции вектора 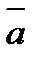 вдоль положительного направления обхода контура L этой поверхности.
вдоль положительного направления обхода контура L этой поверхности.
Пример 6.1.16. Найти циркуляцию векторного поля 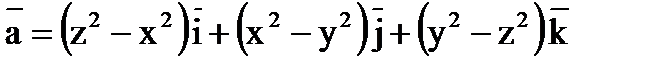
по контуру 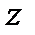 , где
, где 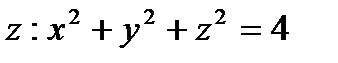 ,
, 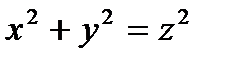
(рис. 6.1.12.)
Решение. Найдем 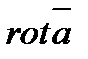 , используя символическую запись (6.1.13)
, используя символическую запись (6.1.13)
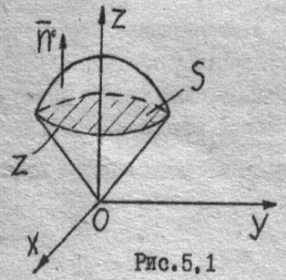
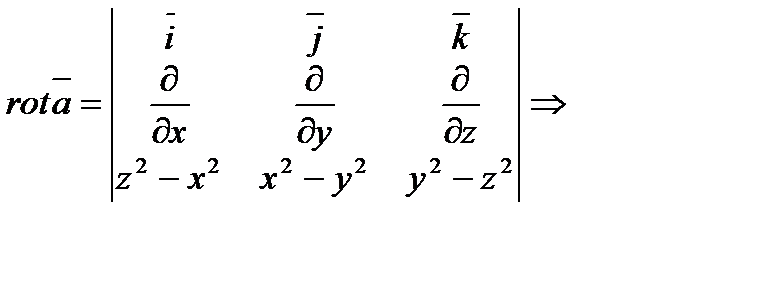
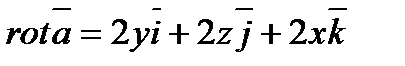 .
.
В качестве поверхности 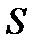 , натянутой на контур
, натянутой на контур 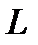 , возьмем круг (в плоскости
, возьмем круг (в плоскости 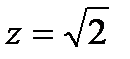 ), тогда
), тогда 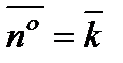 ,
, 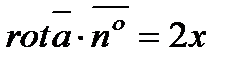 . По формуле (6.1.14) найдем циркуляцию, вычислив двойной интеграл в полярных координатах:
. По формуле (6.1.14) найдем циркуляцию, вычислив двойной интеграл в полярных координатах:
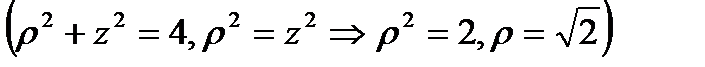 ;
;
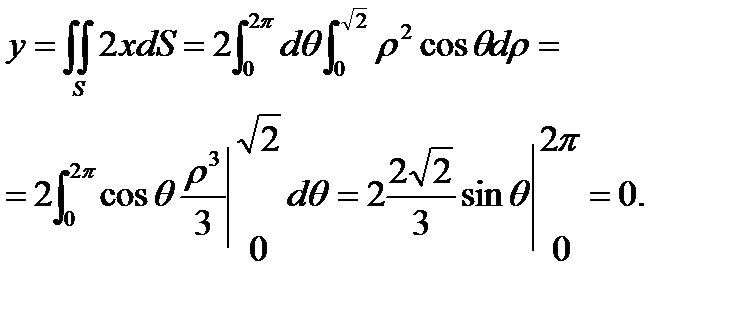

Пример 6.1.17. Вычислить циркуляцию векторного поля 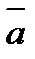 :
: 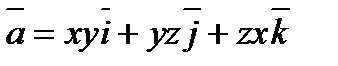 по контуру
по контуру 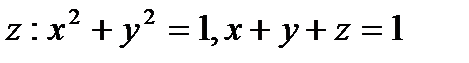 .
.
Решение. Вычислим, применив формулу Стокса (6.1.13). Найдем
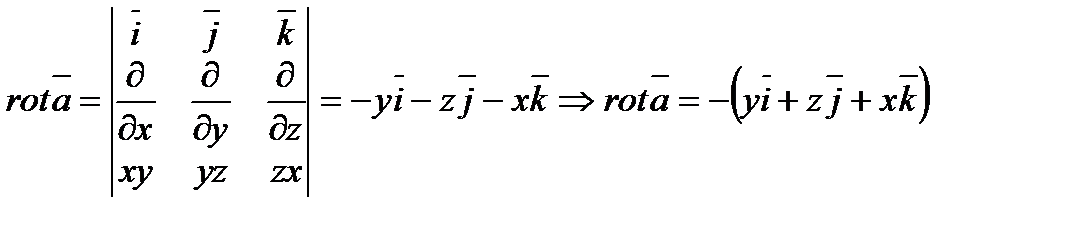 .
.
В качестве поверхности 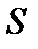 берем часть плоскости
берем часть плоскости 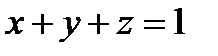 , ограниченную контуром
, ограниченную контуром 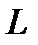 .
.
При пересечении цилиндра 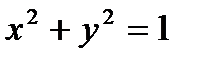 и плоскости
и плоскости 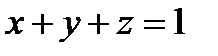 получится эллипс. Поверхность
получится эллипс. Поверхность 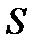 (эллипс) проектируется на плоскость
(эллипс) проектируется на плоскость 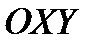 в круг. Тогда
в круг. Тогда 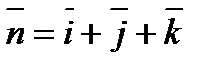 ,
, 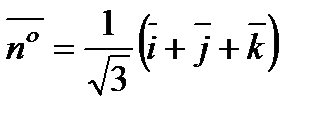 (из уравнения плоскости
(из уравнения плоскости 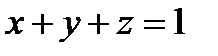 ).
).
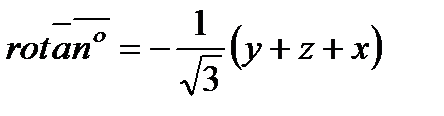 ;
;
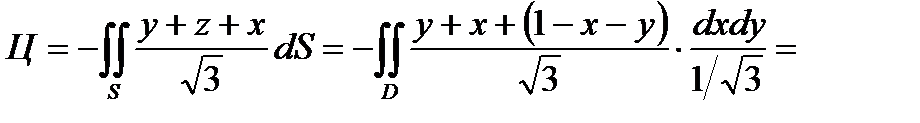
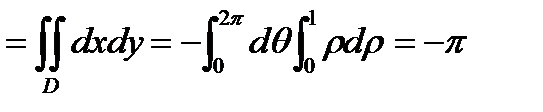 .
.
ЧИСЛОВЫЕ РЯДЫ
Основные понятия
Пусть дана бесконечная числовая последовательность: a1, a2, a3,…, an,…
Выражение, которое получится, если все члены этой последовательности соеденить формально знаком плюс:
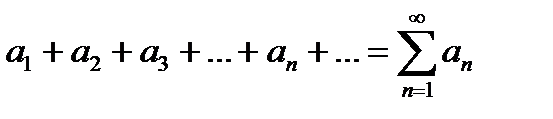 , (6.2.1)
, (6.2.1)
называется числовым рядом (или просто рядом). Часто ряд записывают в виде 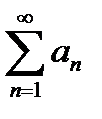 , где указано, что индекс n пробегает все натуральные числа: 1, 2, 3,….
, где указано, что индекс n пробегает все натуральные числа: 1, 2, 3,….
Числа a1, a2, a3,…, an,… называются членами ряда, 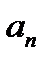 называют общим членом ряда ( при произвольном n!!).
называют общим членом ряда ( при произвольном n!!).
В арифметике и алгебре рассматривают суммы с конечным числом слагаемых. В ряде же слагаемых бесконечно много. Поэтому понятие суммы, состоящей из бесконечного числа слагаемых, требует некоторого специального определения. Что же понимают под выражением (6.2.1) ?
Может оказаться, что иногда это выражение и лишнего чистого смысла.
Введем тонкое определение.
Возьмем сумму n первых членов ряда (6.2.1) и обозначим ее через Sn:
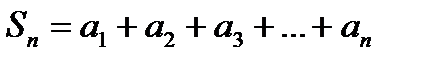 (6.2.2)
(6.2.2)
эту сумму называют n-й частичной суммой ряда (6.2.1). При этом под S1 понимают a1.
Давая в (6.2.2) «n» последовательных значений 1, 2, 3,…, получим последовательность частичных сумм:
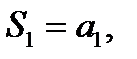
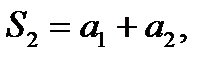
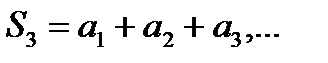
Возможны два случая:
1) либо эта последовательность имеет конечный предел
2) либо она не имеет конечного предела ( стремится к ¥ или вовсе не стремится
ни к какому пределу).
Определение 6.2.1. Если последовательность частичных сумм (или иначе частичная сумма Sn) имеет конечный предел 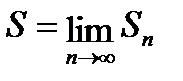 , то ряд (6.2.1) называется сходящимся, а сам этот предел называется суммой ряда.
, то ряд (6.2.1) называется сходящимся, а сам этот предел называется суммой ряда.
При этом пишут: 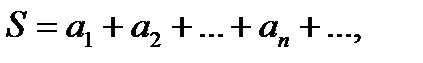 или
или 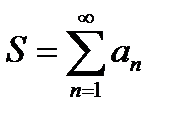 .
.
Если же последовательность частичных сумм не имеет предела то ряд (6.2.1) называется расходящимся.
Расходящийся ряд не имеет суммы в том смысле как мы ее определили.
Однако в том случае когда 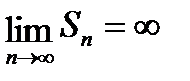 , пишут
, пишут 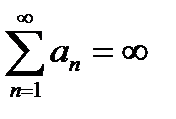 , а также S=¥.
, а также S=¥.
Пример 6.2.1. Пользуясь непосредственно определением суммы ряда, показать, что ряд 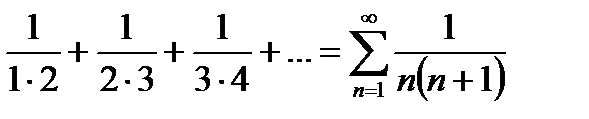 сходится и найти его сумму.
сходится и найти его сумму.
Представим общий член ряда в виде суммы двух дробей:
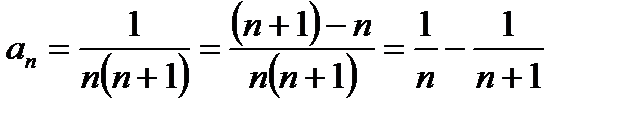
Тогда частичную сумму Sn данного ряда можем переписать так:
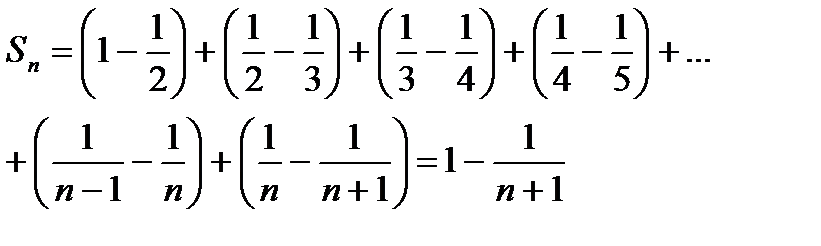
В соответствии с определением надо выяснить существует ли конечный предел Sn при n®¥:
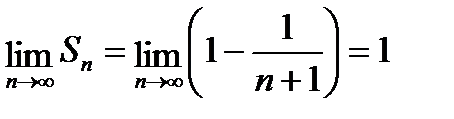
следовательно данный ряд сходится и его сумма S=1.
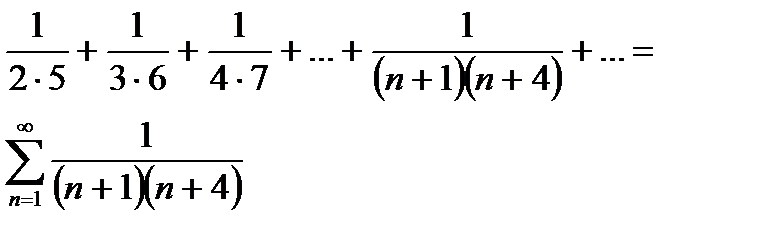
Решение. 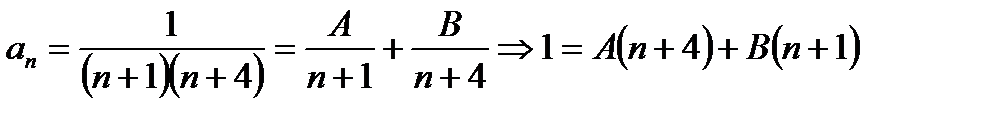 n=-1; A=1/3; B=-1/3.
n=-1; A=1/3; B=-1/3.
Sn-? 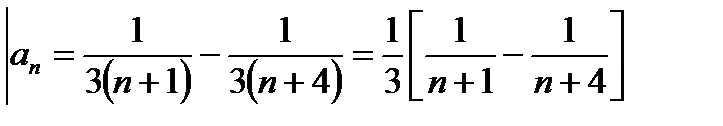
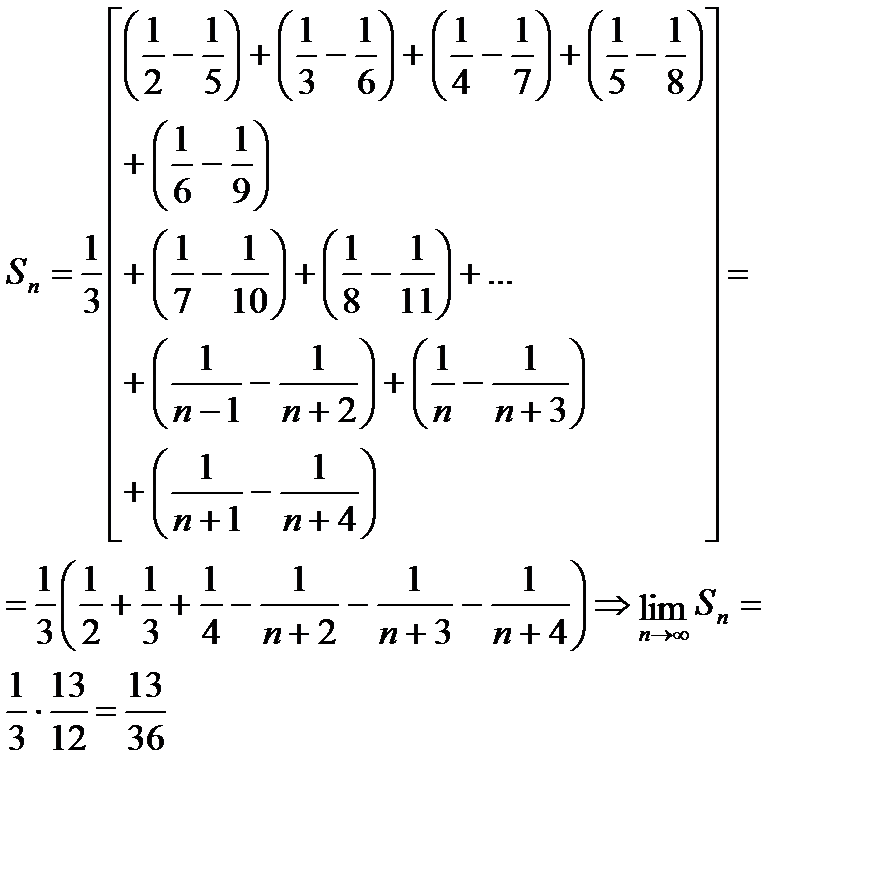
Пример 6.2.2. Исследование сходимости ряда, составленного из членов геометрической прогрессии.
Рассмотрим ряд
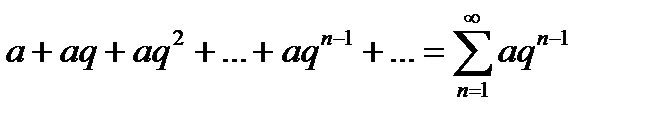 (6.2.3)
(6.2.3)
составленный из членов геометрической прогрессии. Часто данный ряд называют геометрическим рядом.
Выясним, при каких значениях q ряд (6.2.3) сходится.
Составим частичную сумму Sn ряда:
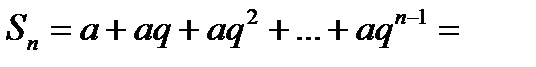 по формуле для суммы n первых членов геометрической прогрессии
по формуле для суммы n первых членов геометрической прогрессии
= 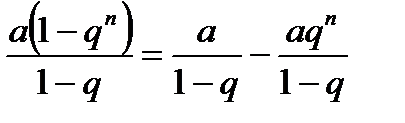 (6.2.4)
(6.2.4)
а) если 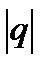 <1 (прогрессия убывающая), то
<1 (прогрессия убывающая), то 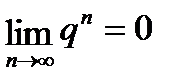 , поэтому
, поэтому 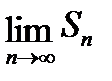 существует и
существует и 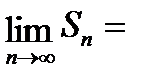
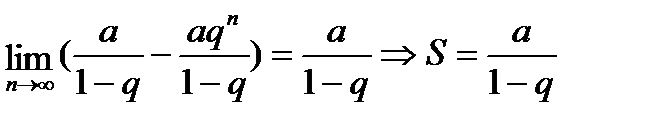
следовательно, в случае, когда 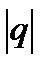 <1, ряд (6.2.3) сходится и его сумма равна
<1, ряд (6.2.3) сходится и его сумма равна 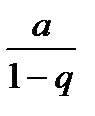 .
.
б) Если 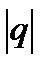 >1, то
>1, то 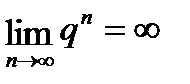 , а тогда (т. к. a¹0) и
, а тогда (т. к. a¹0) и 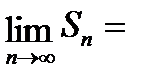
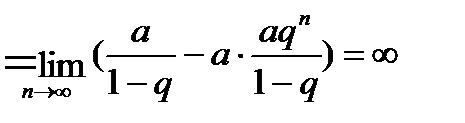
Значит, в случае, когда 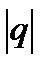 >1, ряд (6.2.3) расходится.
>1, ряд (6.2.3) расходится.
в) если q=-1, то частичная сумма Sn принимает вид: 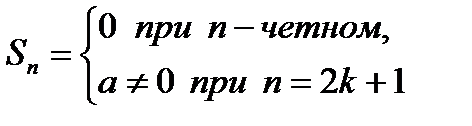
Отсюда ясно что в этом случае Sn при n®¥ предела не имеет и ряд (6.2.3) расходится.
г) При q=1 формула (6.2.4) лишена смысла. Но ясно непосредственно, что в этом случае
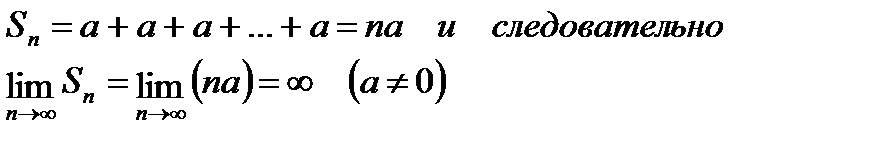
Значит в случае q=1 ряд (6.2.3) также расходится.
Вывод. Итак геометрический ряд 1) сходится при 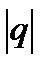 <1 и 2) расходится
<1 и 2) расходится 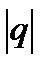 ³1 (a¹0), причем при
³1 (a¹0), причем при 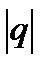 <1 имеем известную (из школьного курса математики) формулу суммы членов бесконечной убывающей геометрической прогрессии.
<1 имеем известную (из школьного курса математики) формулу суммы членов бесконечной убывающей геометрической прогрессии.
