Оценка качества линейной модели регрессии

Основным показателем качества уравнения множественной регрессии является множественный коэффициент детерминации, определяемый по формуле (2.19), либо по формуле в матричных обозначениях:

.

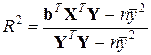(3.18)

Множественный коэффициент детерминации характеризует долю вариации результата Y, обусловленной регрессией, т. е. вариацией всех включенных в модель факторов. Чем ближе R² к единице, тем лучше модель описывает зависимость между факторами и результатом Y.

Показателем качества модели может служить и скорректированный коэффициент детерминации (3.9). Если его значение превышает 0,5, то качество модели считается удовлетворительным.

Проверка значимости уравнения множественной регрессии производится по F-критерию Фишера [см. § 2.3 и формулу (2.21)]. Значимость коэффициентов уравнения проверяется по t-критерию Стьюдента. Стандартная ошибка коэффициента b_j уравнения регрессии определяется по формуле

,

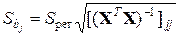(3.19)

где 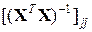— диагональный элемент матрицы .

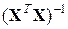Доверительный интервал для истинного параметра b_j имеет вид:

,

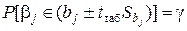(3.20)

где t_таб — табличное значение t-критерия Стьюдента в соответствии с уровнем значимости 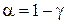и числом степеней свободы остатка 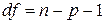(см. приложение 3); g — доверительная вероятность.

Если нижняя граница доверительного интервала имеет отрицательное значение, а верхняя — положительное, то считается, что коэффициент b_j сформировался под влиянием случайных причин, а изменение соответствующего фактора X_j не оказывает существенного влияния на изменение результата Y.

Компьютерные программы обычно рассчитывают для каждого из коэффициентов уравнения регрессии t-статистику Стьюдента

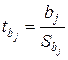(3.21)

и так называемое «P-Значение» — вероятность того, что коэффициент b_j сформировался случайным образом.

Коэффициент b_j признается статистически значимым на уровне значимости a, если выполняется неравенство

,

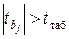(3.22)

где t_таб — табличное значение t-критерия Стьюдента в соответствии с уровнем значимости a и числом степеней свободы 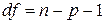(см. приложение 3).

На значимость коэффициента указывает и его «P‑Значение», не превышающее принятый уровень значимости a.

Если значимость коэффициента b_j не установлена, то все выводы относительно него и соответствующего фактора X_j не вполне надежны. Если значение t-статистики при этом больше единицы (по абсолютной величине), то фактор X_j все же считается в какой-то степени информативным. Если же t-статистика по модулю меньше единицы, то фактор X_j следует исключить из модели. Затем уравнение регрессии строится уже без исключенного фактора, все расчеты и анализ при этом повторяются.

Показателями точности модели множественной регрессии также как и парной модели служат стандартная ошибка регрессии S_рег (3.17) и средняя относительная ошибка аппроксимации E_отн (2.23).