Динамика материальной точки и тела, движущегося поступательно 2 страница
Ускорение при гармоническом колебании –
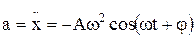 .
.
Амплитуда А результирующего колебания, полученного при сложении двух, происходящих вдоль одной прямой, колебаний с одинаковыми частотами, определяется по формуле
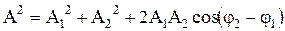 ,
,
где 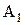 и
и 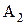 – амплитуды составляющих колебаний;
– амплитуды составляющих колебаний; 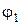 и
и 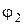 – их начальные фазы.
– их начальные фазы.
Начальная фаза φ результирующего колебания может быть найдена из формулы
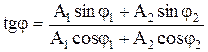 .
.
Частота биений колебаний, возникающих при сложении двух колебаний, происходящих вдоль одной прямой с различными, но близкими по значению частотами 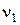 и
и 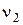 , –
, –
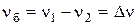 .
.
Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами 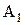 и
и 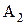 и начальными фазами
и начальными фазами 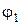 и
и 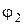 , –
, –
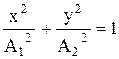 ,
,
т.е. точка движется по эллипсу.
Дифференциальное уравнение гармонических колебаний материальной точки :
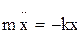 , или
, или 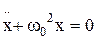 ,
,
где m – масса точки; k – коэффициент квазиупругой силы 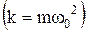 .
.
Полная энергия материальной точки, совершающей гармонические колебания, –
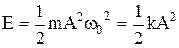 .
.
Период колебаний тела, подвешенного на пружине (пружинный маятник), –
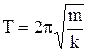 ,
,
где m – масса тела; k – жёсткость пружины.
Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).
Период колебаний математического маятника
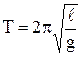 ,
,
где 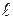 – длина маятника; g – ускорение свободного падения.
– длина маятника; g – ускорение свободного падения.
Период колебаний физического маятника –
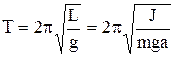 ,
,
где 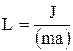 – приведённая длина физического маятника; J – момент инерции колеблющегося тела относительно оси колебаний; a – расстояние от центра масс маятника до оси колебаний.
– приведённая длина физического маятника; J – момент инерции колеблющегося тела относительно оси колебаний; a – расстояние от центра масс маятника до оси колебаний.
Эти формулы являются точными для случая бесконечно малых амплитуд. При конечных значениях они дают лишь приближенные результаты. При амплитудах не более ~ 30 погрешность в значении периода не превышает 1%.
Период крутильных колебаний тела, подвешенного на упругой нити, –
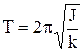 ,
,
где J – момент инерции тела относительно оси, совпадающей с упругой нитью; k – жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.
Дифференциальное уравнение затухающих колебаний :
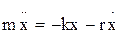 , или
, или 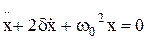 ,
,
где r – коэффициент сопротивления; δ – коэффициент затухания, 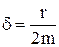 ;
;
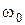 - собственная круговая частота колебаний,
- собственная круговая частота колебаний, 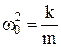 .
.
Решение дифференциального уравнения затухающих колебаний –
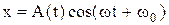 ,
,
где А(t) – амплитуда затухающих колебаний в момент времени t; w - круговая частота затухающих колебаний в момент t.
Круговая частота затухающих колебаний –
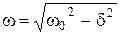
Зависимость амплитуды затухающих колебаний от времени –
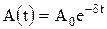 ,
,
где 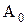 - амплитуда колебаний в момент t=0.
- амплитуда колебаний в момент t=0.
Логарифмический декремент затуханий :
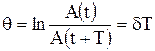 ,
,
где A(t) и A(t+T) – амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.
Дифференциальное уравнение вынужденных колебаний :
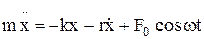 , или
, или 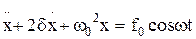 ,
,
где 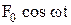 – внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания;
– внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания; 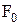 – её амплитудное значение,
– её амплитудное значение, 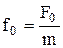 .
.
Амплитуда вынужденных колебаний :
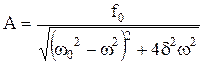 .
.
Резонансная частота и резонансная амплитуда :
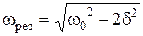 и
и 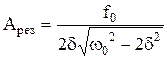 .
.
1.2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Уравнение движения материальной точки вдоль оси имеет вид x = A + Bt + Ct3, где А =2 м, В = 7м/с; С = -0,5м/с3. Найти координату x, скорость v и ускорение a точки в момент времени t, равный 2 с.
Решение. Координату x найдем, подставив в уравнение движения числовые значения коэффициентов А,В,С и времени t:
x=(2+7∙2-0,5∙23)=12 м.
Мгновенная скорость есть первая производная от координат по времени:
v = 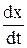 = B +3Ct2.
= B +3Ct2.
Ускорение точки найдем, взяв первую производную от скорости по вре- мени:
a = 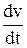 = 6Ct2.
= 6Ct2.
В момент времени t=2с
v =(7-3∙0,5∙22) = 1м/с;
a = 6 · 0,5 ·2 = 6 м/с2.
Пример 2. Тело брошено со скоростью v0 = 10 м/с под углом α = 400 к горизонту. Пренебрегая сопротивлением воздуха, найти:
1) высоту h подъема тела; 2) дальность S полета тела (по горизонтали);
3)время движения тела.
Решение. Перемещение тела можно разложить на два: горизонтальное вдоль оси x и вертикальное вдоль оси y (см. рисунок). Применяя закон независимости движений, имеем
h = 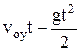 ; (1)
; (1)
S = vox · 2t, (2)
где t – время подъема; 2t – время полета.
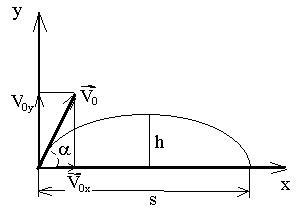
Из рисунка видно, что v0y =v0sinα; v0x = v0cosα . В верхней точке подъема vy = 0, и из уравнения vy = v0y – gt получаем, что v0sin α = gt. Отсюда время подъема равно
t = 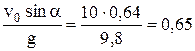 c.
c.
Подставив значение t в (1), получим высоту, на которую поднимется тело:
h= 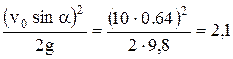 м.
м. 
Подставив значение t в (2), найдем дальность полета:
S = v0 cosα 2t = 10·0,77·1,3 = 10м.
Время полета 2t = 2 · 0,64 = 1,3 с.
Пример 3.Диск радиусом R =5 см вращается вокруг неподвижной оси так, что зависимость угловой скорости от времени задается уравнением
ω = 2At + 5Bt4, где А = 2 рад/с2, В = 1 рад/с5.
Найти для точек на ободе диска к концу первой секунды после начала движения: 1) полное ускорение; 2) число оборотов диска.
Решение. Полное ускорение может быть найдено как геометрическая сумма тангенциального ускорения 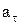 , направленного по касательной к траектории, и нормального ускорения an, направленного к центру кривизны траектории, см. рисунок.
, направленного по касательной к траектории, и нормального ускорения an, направленного к центру кривизны траектории, см. рисунок.
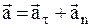 .
.
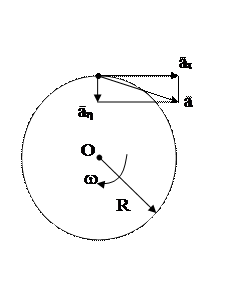 | Так как векторы 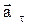 и и 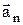 взаимно перпендикулярны, то модуль ускорения – взаимно перпендикулярны, то модуль ускорения – 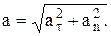 Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами 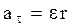 ; ; 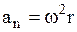 , где ε – угловое ускорение тела; ω – угловая скорость тела. , где ε – угловое ускорение тела; ω – угловая скорость тела. |
По условию задачи
ω = 2 Аt + 5 Bt4.
Следовательно,
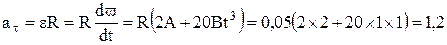 м/с2;
м/с2;
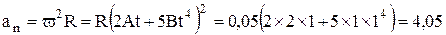 м/с2.
м/с2.
Полное ускорение
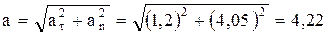 м/с2.
м/с2.
Угол поворота диска равен φ = 2πN (где N –число оборотов), но угловая скорость составляет
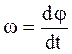 .
.
Следовательно,
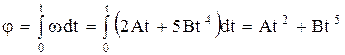 .
.
Тогда число оборотов диска –
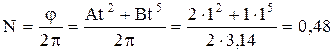 .
.
Пример 4.Маховик вращается с постоянной частотой n0=10 c-1. При торможении он начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова стало равномерным, но уже с частотой n = 6c-1. Найти угловое ускорение ε маховика и продолжительность t торможения, если за время равнозамедленного движения маховик сделал N=50 оборотов.
Решение. Угловое ускорение маховика связано с начальной 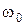 и конечной ω угловыми скоростями соотношением
и конечной ω угловыми скоростями соотношением 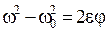 ; откуда
; откуда 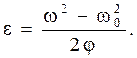
Но так как φ = 2 π N, ω = 2 π n, то
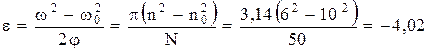 рад/с2.
рад/с2.
Знак «минус» указывает на то, что маховик вращается замедленно.
Для определения продолжительности торможения используем формулу, связывающую угол поворота со средней угловой скоростью вращения и временем: φ = ωсрt. По условию задачи угловая скорость линейно зависит от времени, и поэтому wср можно выразить так:
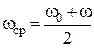 ,
,
тогда 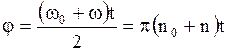 . Откуда
. Откуда
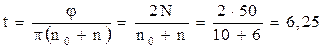 с.
с.
Пример 5.К нити подвешен груз массой m=1 кг. Найти силу натяжения нити 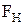 , если нить с грузом: 1) поднимать с ускорением a=5 м/с2; 2) опускать с тем же ускорением.
, если нить с грузом: 1) поднимать с ускорением a=5 м/с2; 2) опускать с тем же ускорением.
 Решение. На поднимаемый груз, действуют сила тяжести mg (вниз) и сила натяжения нити FH (вверх), см. рисунок. Применив второй закон Ньютона, получим, что ma=FH-mg. Отсюда
Решение. На поднимаемый груз, действуют сила тяжести mg (вниз) и сила натяжения нити FH (вверх), см. рисунок. Применив второй закон Ньютона, получим, что ma=FH-mg. Отсюда 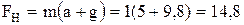 H.
H.
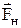 На опускаемый груз также действуют сила тяжести mg (вниз)
На опускаемый груз также действуют сила тяжести mg (вниз)
и сила натяжения нити FH (вверх). Применив второй закон Нью-
тона, получим, что 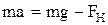 . Отсюда
. Отсюда 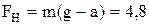 H.
H.
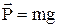
Пример 6.По плоскости с углом наклона 300 к горизонту скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения k = 0,15.
Решение
| Уравнение движения тела в векторной форме (второй закон Ньютона): 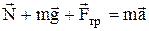 . В проекциях на оси x и y это уравнение примет вид . В проекциях на оси x и y это уравнение примет вид 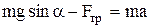 ; (1) ; (1) 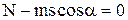 . (2) . (2) |
 Из уравнения (2)
Из уравнения (2) 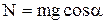 , см. рисунок. Сила трения
, см. рисунок. Сила трения
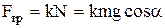 .
.
Тогда, подставив 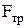 в уравнение (1), получим выражение
в уравнение (1), получим выражение
mgsinα-kmgcosα=ma,
отсюда a=g(sinα-kcosα).
Скорость тела 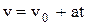 , но v0=0; поэтому
, но v0=0; поэтому
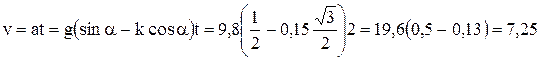 м/с.
м/с.
Пример 7.После абсолютно упругого соударения тела массой m1, движущегося поступательно, с покоящимся телом массой m2 оба тела разлетаются симметрично относительно направления вектора скорости первого тела до удара. Определить, при каких значениях 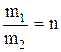 это возможно. Угол между векторами скоростей тел после удара равен 600 , см. рисунок.
это возможно. Угол между векторами скоростей тел после удара равен 600 , см. рисунок.
Решение. Удар абсолютно упругий, и импульс системы постоянен:
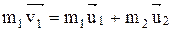
 | В проекциях на оси X и Y 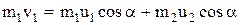 ; (1) ; (1) 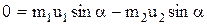 . (2) Из уравнения (2) следует, что . (2) Из уравнения (2) следует, что 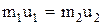 . (3) . (3) |
Уравнение (1) примет вид 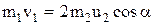 .
.
Закон сохранения кинетической энергии, поскольку удар – абсолютно упругий, имеет вид
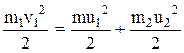 . (4)
. (4)
Подставляя в (4) уравнение (3) при замене 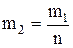 , получаем:
, получаем:
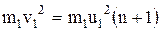 ;
;
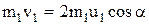 .
.
Уравнения образуют систему, совместное решение которой дает следующий результат:
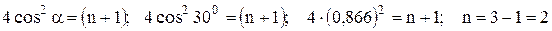 .
.
Пример 8.Шар массой m1, движущийся горизонтально с некоторой скоростью v1, столкнулся с неподвижным шаром массой m2. Шары – абсолютно упругие, удар прямой. Какую долю своей кинетической энергии первый шар передал второму?
Решение. Доля энергии, переданной первым шаром второму, выразится соотношением
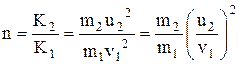 , (1)
, (1)
где K1 – кинетическая энергия первого шара до удара; u2 и K2 – скорость и кинетическая энергия второго шара после удара.
При ударе абсолютно упругих тел одновременно выполняются два закона сохранения: импульса и механической энергии. По закону сохранения импульса, с учетом того, что второй шар до удара покоился, имеем
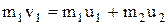 .
.
По закону сохранения механической энергии –
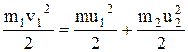 .
.
Решая совместно два последних уравнения, найдём, что
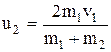 .
.
Подставив выражение 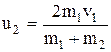 в равенство (1), получим
в равенство (1), получим
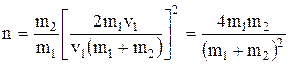 .
.
Из этого соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров.
Пример 9.Сплошной шар массой 1 кг и радиусом 0,05 м вращается вокруг оси, проходящей через его центр. В точке, наиболее удалённой от оси вращения, на шар действует сила, касательная к поверхности. Угол поворота шара меняется по закону 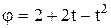 . Определить величину действующей силы, тормозящий момент, время равнозамедленного движения.
. Определить величину действующей силы, тормозящий момент, время равнозамедленного движения.
Решение. Согласно основному закону динамики вращательного движения вращающийся момент равен 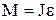 , где J – момент инерции шара; ε – угловое ускорение. Момент инерции шара:
, где J – момент инерции шара; ε – угловое ускорение. Момент инерции шара:
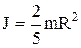 .
.
Угловое ускорение – 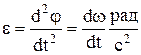 .
.
 Следовательно,
Следовательно, 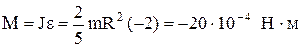 .
.
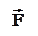
|
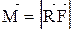 , где
, где 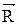 - радиус – вектор, проведённый из этой точки в точку
- радиус – вектор, проведённый из этой точки в точку 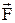 приложения силы. Модуль момента
приложения силы. Модуль момента
силы, как видно из рисунка, 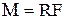 . Отсюда
. Отсюда
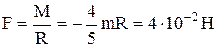 .
.
В момент остановки шара ω=0,
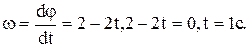
Пример 10.Найти линейное ускорение шара, скатывающегося без скольжения с наклонной плоскости. Угол наклона плоскости a=300, начальная скорость v0=0.
Решение. При скатывании шара с наклонной плоскости высотой h его потенциальная энергия уменьшается, переходя в кинетическую поступательного и
вращательного движения:
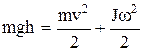 , (1)
, (1)
где J – момент инерции шара. Так как 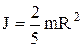 и
и 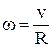 , где R – радиус шара, то уравнение (1) можно записать так:
, где R – радиус шара, то уравнение (1) можно записать так:
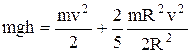 ,
,
т.е. 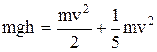 .
.
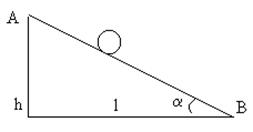
Из рисунка видно, что h=lsinα; тогда 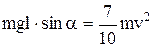 ;
;
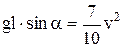 . (2)
. (2)
Так как движение тела происходит под действием постоянной силы, то оно равноускоренное с v0=0 (из условия задачи); поэтому
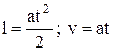 . (3)
. (3)
Подставив (3) в уравнение (2), получим:
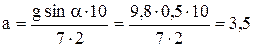 м/с2.
м/с2.
Пример 11.Маховик в виде диска массой m=50 кг и радиусом R = 20 см был раскручен до частоты вращения 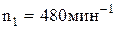 . Вследствие трения маховик остановился. Найти момент M сил трения, считая его постоянным для двух случаев: 1) маховик остановился через t=50 с; 2) маховик до полной остановки сделал N=200 об.
. Вследствие трения маховик остановился. Найти момент M сил трения, считая его постоянным для двух случаев: 1) маховик остановился через t=50 с; 2) маховик до полной остановки сделал N=200 об.
Решение. По основному закону динамики вращательного движения изменение момента импульса вращающегося тела равно произведению момента силы, действующего на тело, на время действия этого момента:
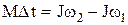 ,
,
где J –момент инерции маховика; 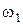 и
и 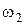 - начальная и конечная угловые скорости. Так как ω2=0 и
- начальная и конечная угловые скорости. Так как ω2=0 и 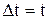 , то Mt=-Jω, откуда
, то Mt=-Jω, откуда
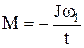 . (1)
. (1)
Момент инерции диска относительно его геометрической оси равен
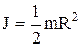 .
.
Подставив это выражение в формулу (1), найдём, что
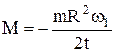 . (2)
. (2)
Выразив угловую скорость ω1 через частоту вращения 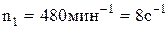 , получим
, получим 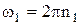 , произведя вычисления по формуле (2), найдём, что
, произведя вычисления по формуле (2), найдём, что
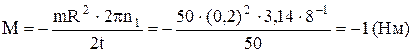 .
.
В условии задачи дано число оборотов маховика до остановки, т.е. его угловое перемещение:
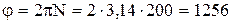 рад.
рад.
Запишем формулу, выражающую связь работы с изменением кинетической энергии:
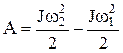 , или ω2=0.
, или ω2=0.
Она примет вид
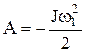 . (3)
. (3)
Работа при вращательном движении определяется по формуле 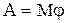 . Подставив выражение работы и момента инерции диска в формулу (3), получим
. Подставив выражение работы и момента инерции диска в формулу (3), получим
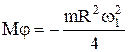 .
.
Отсюда
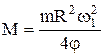 = –1 (Нм) .
= –1 (Нм) .
Знак «минус» показывает, что момент силы трения оказывает тормозящее действие.
Пример 12.Человек стоит в центре круга Жуковского, вращающегося по инерции вокруг неподвижной оси с частотой 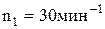 . В вытянутых руках он держит по гире массой m=5кг каждая. Расстояние от каждой гири до оси вращения
. В вытянутых руках он держит по гире массой m=5кг каждая. Расстояние от каждой гири до оси вращения 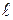
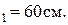 Суммарный момент инерции человека и скамьи относительно оси вращения I0=2 кг×см2. Определить частоту n2 вращения скамьи с человеком. Какую работу совершит человек, если прижмёт гири к себе так, что расстояние от каждой гири до оси станет равным
Суммарный момент инерции человека и скамьи относительно оси вращения I0=2 кг×см2. Определить частоту n2 вращения скамьи с человеком. Какую работу совершит человек, если прижмёт гири к себе так, что расстояние от каждой гири до оси станет равным 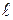 2=20cм?
2=20cм?
Решение. По условию задачи момент внешних сил относительно вертикальной оси вращения равен нулю, поэтому момент импульса системы сохраняется:
I1ω1= I2 ω2,
где 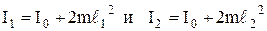 – соответственно момент инерции всей системы до и после сближения; m- масса каждой гири. Угловая скорость ω=2πn. Подставив w в уравнение, получим искомую частоту вращения:
– соответственно момент инерции всей системы до и после сближения; m- масса каждой гири. Угловая скорость ω=2πn. Подставив w в уравнение, получим искомую частоту вращения:
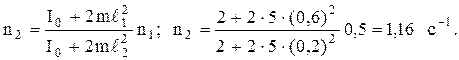
Работа, совершаемая человеком, равна изменению кинетической энергии системы:
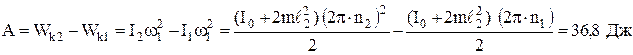 .
.

 N
N 



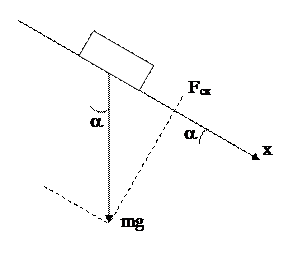 Рис. 4
Рис. 4