Формула пуассона для найпростішого потоку

Імовірність того ,що за проміжок часу t+△t не відбудеться жодна подія ,подається у вигляді

Імовірність того, що за цей самий проміжок часу здійсниться т подій, визначається так

Поділимо ліву і праву частини системи рівнянь на ∆t і вико­наємо граничний перехід при ∆t -0

У результаті дістанемо систе­му лінійних диференціальних рівнянь:

Імовірність того ,що за час t відбудеться m випадкових подій ,які утворюють найпростіший потік ,обчислюється за формулою

P_m(t)= (λt)^m*e^-λt /m! де λ-інтенсивність найпростішого потоку, тобто :середне число подій ,які відбудуться за одиницю часу.

41) Випадкові процеси можна класифікувати залежно від того, плавно чи стрибкоподібно змінюються стани системи, в якій вони відбуваються, скінченна чи нескінченна множина цих станів. Серед випадкових процесів особливе місце посідають марковські випадкові процеси, що становлять основу теорії масового обслуговування.

Випадковий процес називається марковським, якщо для будь-якого моменту часу імовірнісні характеристики процесу в майбутньому залежать лише від його стану в даний момент і не залежать від того, коли і як система набула цього стану.

Приклад. Система — лічильник у таксі. Стан системи в момент t характеризується кількістю кілометрів, пройдених автомобілем до даного моменту. Нехай у момент лічильник показує Імовірність того, що в момент лічильник показуватиме ту чи іншу кількість кілометрів залежить від але не залежить від того, в які моменти часу змінювались покази лічильника до моменту

Деякі процеси можна наближено вважати марковськими.

42). Системи для розвязування однотипних задач називаються системами масового обслуговування -(СМО) Процеси, які при цьому відбуваються, називають процесами обслуговування.Кожна МСО складається з певної кількості обслуговуваних одиниць (пристроїв, пунктів, станцій), які називатимемо каналами обслуговування.За кількістю каналів СМО поділяються на одно- та багатоканальні. Заявки надходять до СМО звичайно не регулярно, а випадково, створюючи так званий випадковийпотік заявок (посилань). Обслуговування заявок також триває протягом певного випадкового часу. З огляду на випадковість потоку заявок і часу обслуговування СМО завантажуються нерівномірно: у певні періоди нагромаджується дуже багато заявок (вони або стають у чергу, або залишають СМО не обслуговуваними), в інші періоди СМО працює з недовантаженням або простоює.

Предметом теорії масового обслуговування є побудова математичних моделей, що пов’язують задані умови роботи СМО з показниками її ефективності, які описують здатність цієї системи обробляти потоки заявок.

СМО поділяються на два основні класи:

СМО з відмовами і СМО з очікуванням (чергою).

У СМО з відмовами заявка, яка надійшла в момент, коли всі канали були зайняті, отримавши відмову, залишає СМО і в подальшому процесі обслуговування не бере участі.

У СМО з очікуванням заявка, що надходить у момент, коли всі канали зайняті, не залишає систему, а стає в чергу на обслуговування.

Процес роботи СМО являє собою випадковий процес.

Процес називається процесом із дискретними станами, якщо його можливі стани можна зарані перелічити, а перехід системи з одного до іншого відбувається миттєво (стрибкоподібно). Процес називається процесом із неперервним часом, якщо моменти можливих переходів системи з одного стану до іншого не фіксовані заздалегідь, а випадкові.

Процес функціонування СМО являє собою випадковий процес із дискретними станами та неперервним часом.

Математичний аналіз роботи СМО істотно спрощується, якщо процес цієї роботи — марковський.

Процеси відновлення

44) Генеральною сукупністю в математичній статистиці називається множина однотипних об’єктів, кількісна чи якісна ознака яких підлягає вивченню. Підмножина об’єктів, дібраних у відповідний спосіб із генеральної сукупності, називається вибірковою сукупністю. Вважаємо, що ознака, яка вивчається, є випадковою величиною Х із функцією розподілу Результати вибірки розглядатимемо як послідовність незалежних однаково розподілених випадкових величин Закон розподілу для всіх визначається функцією Результати вибірки — реалізації випадкових величин — позначатимемо відповідно через Розмістивши ці числа в порядку зростання і записавши частоти з якими зустрічаються ці значення, дістанемо варіаційний, або статистичний, ряд:

			…
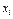Частоти			…

На підставі такого ряду можна побудувати статистичну функцію розподілу Якщо , то статистична функція розподілу збігається д теоретичної функції розподілу.