Представление параметров пассивных элементов и синусоидальных сигналов в комплексной форме

Комплексный ток, напряжение, ЭДС. Задача определения параметров электрического сигнала в цепях синусоидального тока может быть довольно просто решена с привлечением аппарата алгебры комплексных чисел. Для этого синусоидальный сигнал представляют комплексным числом (табл.4.1).

Источник синусоидального напряжения или тока полностью определен, если заданы его комплексная амплитуда либо комплекс действующего значения.

Таблица 3.1 — Комплексный ток, напряжение, ЭДС

Вели- чина	Оригинал (мгновенное значение)	Комплексная гармоническая функция	Комплекс-ная амплитуда	Комплекс действую-щего значения
Ток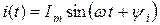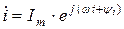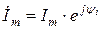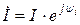
Напря- жение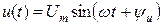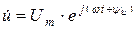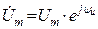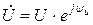
ЭДС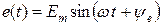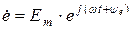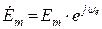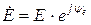

Комплексное сопротивление. Пассивный элемент в цепи синусоидального тока определяется своим комплексным сопротивлением

,

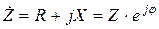где 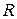— вещественная часть комплексного сопротивления, равная активному сопротивлению цепи;

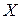— мнимая часть комплексного сопротивления, равная реактивному сопротивлению цепи;

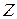— модуль комплексного сопротивления цепи, равен ;

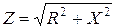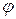— аргумент комплексного сопротивления, равный углу сдвига фаз между током и напряжением, .

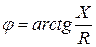Комплексное сопротивление определяется как отношение комплексного напряжения к комплексному току : .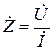

Комплексные сопротивления отдельных пассивных элементов приведены в табл.3.2. Для резистивного элемента комплексное сопротивление 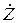является чисто активным, а для индуктивного и емкостного — чисто реактивным.

Таблица 3.2 — Комплексные сопротивления пассивных элементов

Элемент	Оригинал	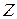Комплексное изображение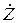
Резистивный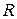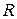
Индуктивный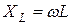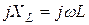
Емкостной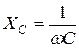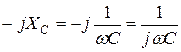

Комплексная проводимость. Пассивный элемент в цепи синусоидального тока может быть определен и такой величиной, как комплексная проводимость

,

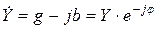где 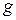— вещественная часть комплексной проводимости, равная активной проводимости цепи;

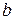— мнимая часть комплексной проводимости, равная реактивной проводимости цепи;

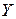— модуль комплексной проводимости цепи, равен ;

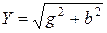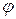— аргумент комплексной проводимости, равный углу сдвига фаз между током и напряжением, взятому с обратным знаком, .

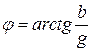Комплексная проводимость — величина, обратная комплексному сопротивлению, определяется как отношение комплексного тока к комплексному напряжению: .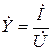

Комплексные проводимости отдельных пассивных элементов приведены в табл.3.3. Для резистивного элемента комплексная проводимость 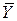является чисто активной, а для индуктивного и емкостного — чисто реактивной.

Таблица 3.3 — Комплексные проводимости элементов

Элемент	Оригинал	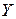Комплексное изображение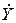
Резистивный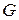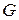
Индуктивный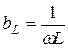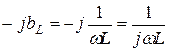
Емкостной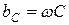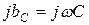

Связь между комплексным сопротивлением и проводимостью. Установим соответствие между величинами комплексного сопротивления и проводимости:

; ; ;

; ; .

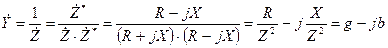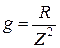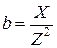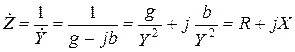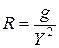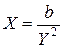Мощность в линейной 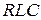-цепи синусоидального тока. Для цепи с напряжением на участке цепи 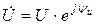и током 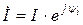полная мощность в комплексной форме определяется следующим образом:

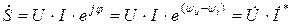
Модуль полной мощности в линейной цепи синусоидального тока определяется по формуле:

,

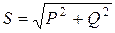где 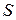— полная мощность, измеряется в Вольт-Амперах (ВА);

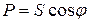— активная составляющая полной мощности, измеряется в Ваттах (Вт);

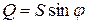— реактивная составляющая полной мощности, измеряется в Вольт-Амперах реактивных (ВАР).