Критерий устойчивости Найквиста

Критерий Найквиста ориентирован на представление динамических свойств системы в виде структуры с единичной обратной связью (рис.2.1). Для анализа устойчивости положения равновесия в нуле и, следовательно, устойчивости всех других решений линейного ДУ

Д(p)y(t) = B(p) ν(t), p ≡ d/dt, (2.9)

он использует амплитудно-фазовую характеристику 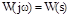, 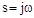разомкнутой системы и число q правых корней в характеристическом уравнении разомкнутой системы

D(p)=Д(p)–B(p)=0. (2.10)

Условия устойчивости для статических систем по критерию Найквиста формулируются следующим образом.

Пусть система, показанная на рис. 2.1, устойчива в разомкнутом состоянии, q = 0. Она будет устойчива в замкнутом состоянии тогда и только тогда, когда АФХ W(jω) не охватывает критическую точку (-1,j0). Если же АФХ охватывает критическую точку (-1,j0), то система неустойчива в замкнутом состоянии.

Если АФХ проходит через т.(-1,j0), то в характеристическом уравнении замкнутой системы имеется пара чисто мнимых корней, а остальные левые. Последний вариант соответствует критическому случаю теорем Ляпунова об анализе устойчивости по уравнениям 1-го приближения. На рис. 2.2 приведены кривые иллюстрирующие поведение АФХ для случая 1 – устойчивой, 2 – неустойчивой и 3 – критический случай (граница устойчивости линейной системы).

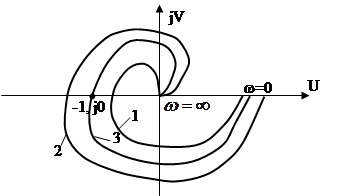Рис. 2.2.

Для анализа устойчивости астатических систем их АФХ

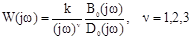
в разомкнутом состоянии на комплексной плоскости приходится дополнять дугами радиуса R = ∞ и центральным углом, равным νπ/2, отсчитываемым от положительного направления вещественной оси по направлению часовой стрелки. На рис. 2.3 приведены АФХ с их дополнениями систем с порядком астатизма ν = 1 (рис.2.3,а) и ν= 2 (рис. 2.3,б).

После дополнения АФХ астатических систем удовлетворяют условиям устойчивости, приведенным для статических систем.

Степень удаления АФХ устойчивой системы от критической точки (-1,j0) оценивается по величине запасов устойчивости по амплитуде и фазе.

Запасом устойчивости по фазе называют дополнение γ угла φ(ω_с), где ω_с – частота среза, до значения –π по часовой стрелке. Численно запас γ определяется выражением γ = π + φ (ω_с). Частота среза определяется условием | W(jω_c) | = R(ω_c) = 1.

Запасом устойчивости по амплитуде называют минимальную из величин (R(ω_π1),R^-1(ω_π2)), где частоты 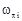определяются условием

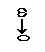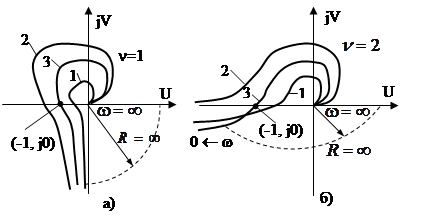Рис. 2.3.

φ(ω) = - π, наименее удаленные от критической точки (-1,j0).

Запасы устойчивости удобно определять графически. Для этого на комплексной плоскости с годографом вектора W(jω),ω 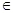[0,∞) проводят окружность единичного радиуса с центром в начале координат плоскости. В точке пересечения окружности и АФХ частоты ω = ω_с, arg W(jω_с) = φ(ω_c). По графику непосредственно определяются запас по фазе γ и запас по амплитуде H = min (H₁ и h^-1), как это показано на рис.2.4.

Если вместо АФХ разомкнутой системы использовать ее логарифмические частотные характеристики, то для систем с АФХ I-рода условия устойчивости принимают вид: а) устойчивость ω_с<ω_π; б) неустойчивость ω_с>ω_π1; в) граница устойчивости ω_с=ω_π.

Для сложных систем используется правило переходов Я.З.Цыпкина [5].

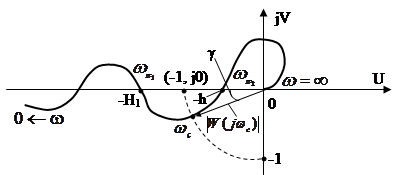Рис. 2.4