Пуассоновские потоки событий

10. Для анализа изменения с течением времени размера текущего фонда компании, ведущей дела по автострахованию, важно обладать информацией о процессе поступлений в компанию требований по выплатам в соответствии со страховыми полисами.

Наблюдение за работой компании в предшествующий период показало, что число поступающих в компанию требований по выплатам за любой промежуток времени длиной τ не зависит от момента времени, с которого начинается отсчет промежутка τ, а зависит только от его продолжительности; требования в компанию в любые два непересекающиеся интервалы времени поступают независимо; в достаточно малые промежутки времени в компанию поступает по одному требованию. Ожидаемое число требований, поступающих в компанию за неделю, равно 2.

Какова вероятность того, что:

1) за месяц в компанию поступит 7 требований;

2) за месяц в компанию поступит менее 7 требований;

3) за месяц в компанию поступит не менее 7 требований;

4) за неделю в компанию не поступит ни одного требования;

5) за две недели в компанию поступит хотя бы одно требование;

6) интервал времени между двумя соседними требованиями будет менее двух дней;

7) интервал времени между двумя соседними требованиями будет не менее двух дней.

Решение. Сначала определим, каким является поток требований по выплатам.

По условию число поступающих в компанию требований по выплатам за любой промежуток времени не зависит от начала этого промежутка, а зависит лишь от его длины. Поэтому поток стационарен.

Поскольку требования за любые два непересекающиеся интервала времени поступают независимо, то поток обладает свойством отсутствия последействия.

Так как в достаточно малые промежутки времени в компанию поступает по одному требованию, то поток одинарен.

Таким образом, рассматриваемый поток является стационарным пуассоновским, т.е., простейшим потоком, и к нему можно применить формулы из теорем 1,2,3 лекций. За единицу времени естественно принять одну неделю.

По условию интенсивность потока равна 2 требования в неделю.

Пусть X(τ) – число требований по выплатам, поступающих в компанию за промежуток τ (недель), и Т – промежуток времени между любыми двумя соседними требованиями.

1) В первом вопросе τ = 1 месяц = 4 недели и m = 7. Тогда по формуле 2 из имеющейся таблицы 1 получаем

p_m(τ) = 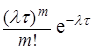, т.е. p₇(4) = 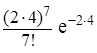≈ 0,143.

2) По формуле 4 из таблицы 1

Р(Х < k) = 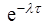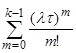, т.е. Р(Х(4) < 7) =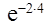 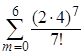≈ 0,321.

3) По формуле 5 из таблицы 1

Р(Х(4) ≥ 7) = 1 – Р(Х(4) < 7) = 1 – 0,321 = 0,679.

4) В четвертом вопросе τ = 1 неделя. Вероятность p₀(1) того, что за неделю в компанию не поступит ни одного требования по выплатам, вычисляется по формуле 2 из таблицы 1.

p₀(τ) = 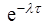, т.е. p₀(1) = 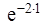≈ 0,135.

5) В пятом вопросе τ = 2 недели. Вероятность Р(Х(2) ≥ 1) того, что за две недели в компанию поступит хотя бы одно требование, вычисляем по формуле 6 из таблицы 1.

Р(Х(2) ≥ 1) = 1 - 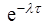, т.е. Р(Х(2) ≥ 1) = 1 - 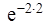≈ 0,981.

6) Вероятность того, что Т меньше двух дней или 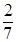недели, вычисляем с помощью формулы для функции распределения из теоремы 3 §4.

F(t) = P(T < t) = 1 - 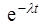, т.е. P(T < 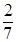) = F( 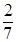) = 1 – 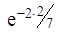≈ 0,393.

7) Вероятность того, что Т не меньше двух дней или 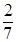недели, вычисляем с помощью формулы для функции распределения из теоремы 3 §4.

P(T ≥ 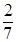) = 1 – P(T < 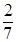) = 1 – 0,393 = 0,607. ►

11. Число вкладов частных лиц в банк за любой определенный промежуток времени, как показали предыдущие наблюдения, не зависят от начала этого промежутка, а зависят лишь от его продолжительности. Вклады в банк в любые два непересекающихся промежутка времени делаются независимо. В промежутки времени достаточно малой длины вклады в банк поступают по одному. Средний интервал времени между двумя соседними вкладами равен 3-м часам.

Найти вероятности, с которыми:

1) за два дня в банк будет сделано 5 вкладов;

2) за два дня в банк будет сделано менее 5 вкладов;

3) за два дня в банк будет сделано не менее 5 вкладов;

4) за день в банк не будет сделано ни одного вклада;

5) за три дня в банк будет сделан хотя бы 1 вклад;

6) промежуток времени между двумя соседними вкладами в банк составит менее 3-х часов;

7) промежуток времени между двумя соседними вкладами в банк составит не менее 3-х часов.

Решение. Сначала по формуле математического ожидания из теоремы 3 найти интенсивность потока λ. Временная единица день приравнивается к 8 рабочим часам.

p₅(16) ≈ 0,174;

Р(Х(16) < 5) ≈ 0,384;

Р(Х(16) ≥ 7) ≈ 0,616;

p₀(8) ≈ 0,069;

Р(Х(24) ≥ 1) ≈ 0,999;

P(T < 3) ≈ 0,632;

P(T ≥ 3) ≈ 0,368.►

12. Проанализируем поток поступлений в страховую компанию, занимающуюся автострахованием, требований по выплатам в соответствии со страховыми полисами за период с начала ноября по конец января. Изучение этого потока в рассматриваемый период в прошлые годы показало, что число требований по выплатам, поступающих за некоторый промежуток времени τ, зависит не только от его продолжительности, но и от его начала. Объясняется это тем, что в рассматриваемый период ухудшаются погодные условия, обстановка на дорогах, что ведет к увеличению дорожно-транспортных происшествий.

Независимость поступлений требований в любые непересекающиеся интервалы времени и поступление требований по одному в малые промежутки времени сохраняются и в данной ситуации.

Ожидаемое число требований, поступающих в компанию за неделю, зависит от времени следующим образом: λ(t) = .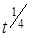

С какой вероятностью

1) за ноябрь месяц поступит в компанию 6 требований;

2) за декабрь месяц поступит в компанию 6 требований;

3) за январь месяц поступит в компанию не менее 5 требований;

4) за первые две недели ноября не поступит ни одного требования;

5) за вторую и третью недели декабря поступит хотя бы одно требование;

6) интервал времени между двумя соседними поступлениями требований будет не менее трех дней, если первое из них поступило в первый день второй недели января;

7) интервал времени между двумя соседними поступлениями требований будет менее двух дней, если первое из них поступило в первый день третьей недели декабря.

Решение. Поток требований является пуассоновским, но не стационарным.

За единицу времени примем одну неделю.

Пусть Х(t₀, τ) – случайное число поступивших в компанию требований за промежуток времени от t₀ до t₀ + τ, а Т(t₀) – случайный интервал времени между двумя соседними требованиями, первое из которых поступило в момент времени t₀.

Имеем следующую картинку распределения временных промежутков за рассматриваемый период:

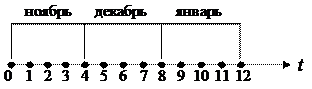1) В первом вопросе τ = 1 месяц = 4 недели, момент начала этого промежутка t₀ = 0, m = 6.

По формуле 2 из таблицы 2 математическое ожидание а = М(Х(0; 4)) случайной величины Х(0; 4) равно

а =М(Х(0; 4)) = 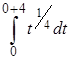= = 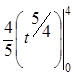= 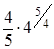4,525.

Теперь по формуле 3 из таблицы 2можно найти требуемую вероятность

Р₆(0; 4) = 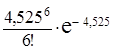≈ 0,129.

2) Во втором вопросе τ = 1 месяц = 4 недели, t₀ = 4, m = 6. По формуле 2 таблицы 2

а =М(Х(4; 4)) = 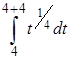= = 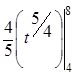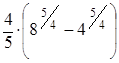≈ 6,238.

Тогда по формуле 3 таблицы 2

Р₆(4; 4) = 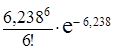≈ 0,16.

3) В третьем вопросе τ = 1 месяц = 4 недели, t₀ = 8, k = 5. По формуле 2 таблицы 2

а =М(Х(8; 4)) = 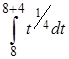= = 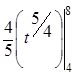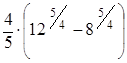≈ 7,104.

Искомую вероятность Р(Х(8,4) ≥ 5) находим по формуле 6 таблицы 2

Р(Х(8,4) ≥ 5) = 1 - 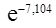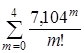≈ 0,836.

4) В четвертом вопросе τ = 2 недели, t₀ = 0, m = 0.

а =М(Х(0; 2)) = 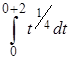= = 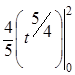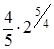≈ 1,903.

Тогда по формуле 4 таблицы 2

p₀(0, 2) = 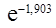≈ 0,149.

5) В пятом вопросе τ = 2 недели, t₀ = 5.

а =М(Х(5; 2)) = 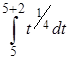= = 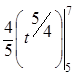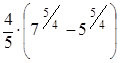≈ 3,127.

Тогда по формуле 7 таблицы 2

Р(Х(5,2) ≥ 1) = 1 - 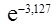≈ 0,956.

6) В шестом вопросе τ = 3 дня = 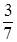недели, t₀ = 9.

а =М(Х(9; 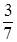)) = = 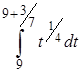= 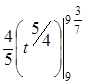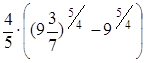≈ 0,747.

Тогда искомую вероятность находим по формуле (1) §5

P(T(9) ≥ 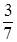) = ℮^{- 0,747} ≈ 0,474.

7) В седьмом вопросе τ = 2 дня = 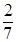недели, t₀ = 6.

а =М(Х(6; 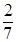)) = = 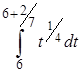= 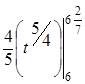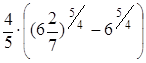≈ 0,45.

Тогда

P(T(6) < 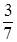) = 1 – P(T(6) ≥ 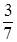) = 1 – ℮^{- 0,45} ≈ 0,362.►

13. Ответить на вопросы предыдущего примера, если в его условии ожидаемое число требований, поступающих в компанию за месяц, зависит от времени t следующим образом: λ(t) = .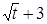

Ответ. За единицу времени принять 1 месяц.

Р₆(0; 1) ≈ 0,086;

Р₆(1; 1) ≈ 0,115;

Р(Х(2,1) ≥ 5) ≈ 0,482;

p₀(0, 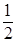) ≈ 0,176;

Р(Х(1 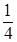, 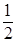) ≥ 1) ≈ 0,879;

P(T(2 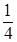) ≥ ) 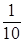≈ 0,452;

P(T(1 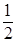) < ) 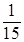≈ 0,246.►

Потоки Эрланга.

14. Рассмотрим деятельность некоторого рекламного агентства. Для формулирования рекомендаций по улучшению его работы полезно обладать информацией о потоке поступления заказов на изготовление и размещение рекламы. Поэтому велись наблюдения, в частности, за интервалом времени между соседними поступлениями заказов, представляющим собой непрерывную случайную величину. Обозначим ее через Т. В результате статистической обработки этих данных были получены следующие характеристики случайной величины Т: среднее значение интервалов времени Т между двумя соседними поступлениями заказов М(Т) = 1 неделя и среднее квадратическое отклонение σ(Т) = 4 дня.

Заменим поток заказов нормированным потоком Эрланга 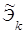, обладающим приближенно теми же характеристиками, найдем его интенсивность 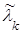, порядок k и плотность распределения 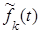; подсчитаем вероятность того, что промежуток времени между двумя соседними заказами больше трех и меньше пяти дней.

Итак, для потока 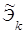имеем.

М( 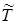) = 1 неделя, σ( 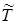) = 4 дня = 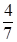недели. По формулам 2 и 5 из таблицы 3 для нормированного потока

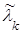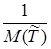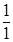= λ = = = 1 (заказ в неделю).

По формулам 7 и 2 для нормированного потока таблицы 3 имеем

σ( ) = = =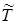

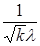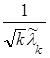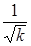
откуда

k = 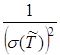= 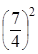≈ 3.067.

Так как k – порядок нормированного потока Эрланга, то k должно быть натуральным числом. Поэтому в качестве k естественно выбрать ближайшее натуральное число, т.е. k = 3.

Таким образом, данный поток заказов можно приближенно заменить нормированным потоком Эрланга третьего порядка 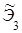с интенсивностью 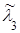=1 заказ в неделю.

Для плотности распределения случайной величины 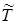по формуле 3 из таблицы 3 для нормированного потока получим выражение

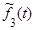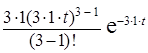= = 13,5∙t²∙℮^-3t (t > 0).

Исследовав стандартным методом функцию 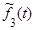, найдем, что она

1) определена на (0, +∞),

2) является функцией общего вида,

3) возрастает на промежутке 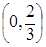и убывает на промежутке ;

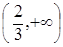4) точка t = 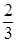является точкой максимума, а сам максимум равен 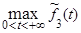=0,812,

5) точки t₁ = 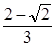и t₂ = 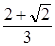являются точками перегиба графика функции, значения функции в этих точках равно 0,287 и 0,575 соответственно,

6) 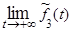= 0, т.е. ось 0t является для графика функции горизонтальной асимптотой.

Построим график функции.

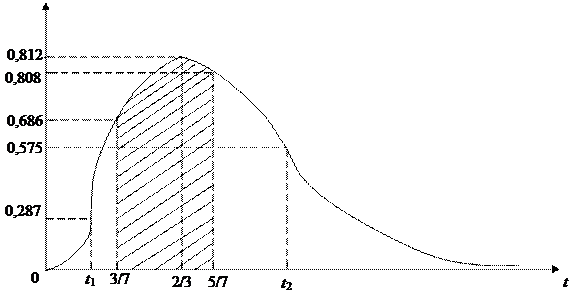Вероятность р = 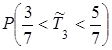того, что интервал времени между двумя соседними заказами больше трех и меньше пяти дней, равна по значению площади заштрихованной на рисунке криволинейной трапеции, которая вычисляется по формуле

р = 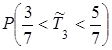= = 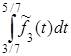13,5 .

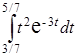Интегрируем по частям

р = 13,5∙ 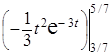+ 13,5∙ =

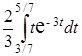=–13,5∙0,003+13,5∙ 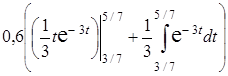=–13,5∙0,003+13,5∙0,17 = 0,189.►

15. Проанализировать ситуацию, рассмотренную в предыдущем примере, если среднее значение интервала Т между двумя соседними поступлениями заказов на рекламу М(Т) = 1,5 недели и среднее квадратическое отклонение σ(Т) = 1 неделя. Найти вероятность того, что промежуток времени между двумя соседними заказами будет меньше двух недель.

Ответ. Поток заказов можно приближенно заменить нормированным потоком Эрланга второго порядка 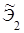с интенсивностью = .

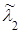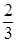Плотность распределения 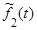= 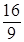∙t∙℮^-2t.

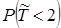≈ 0,404.►