Порівняння нескінченно малих та нескінченно великих величин
Ділення двох нескінченно малих або двох нескінченно великих величин не визначено тому що їх відношення може бути нескінченно малою або нескінченно великою або постійною величиною.
Означення. Нескінченно малі величини 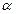 та
та 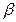 називаються нескінченно малими одного порядку, якщо їх відношення має скінченну границю, відмінну від нуля, тобто якщо
називаються нескінченно малими одного порядку, якщо їх відношення має скінченну границю, відмінну від нуля, тобто якщо 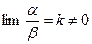 .
.
Означення. Якщо відношення двох нескінченно малих величин є нескінченно мала величина, тобто 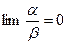 , то
, то 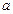 називають нескінченно малою величиною вищого порядку малості в порівняння з
називають нескінченно малою величиною вищого порядку малості в порівняння з 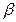 .
.
Знаходження границі відношення двох нескінченно малих або двох нескінченно великих величин називають розкриттям невизначеності їх відношення.
Не слід вважати, що будь-яка змінна величина має границю. Розглянемо, наприклад, послідовність
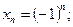
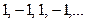
Ця послідовність не має границі тому, що при будь-якому n сусідні два значення цієї змінної відрізняються за модулем на дві одиниці. Отже, для 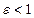 на числовій осі не має такої точи,
на числовій осі не має такої точи,  -окіл якого містив би усі значення х, починаючи з деякого N.
-окіл якого містив би усі значення х, починаючи з деякого N.
Ознаки існування границі змінної величини:
Ознака 1. Якщо в одному процесі змінна величина у заключна між двома іншими змінними х та z, які мають однакову границю а, то й змінна величина у має границю, що дорівнює а. Іншими словами:
якщо 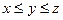 , та
, та 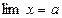 ,
, 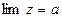 , то у також має границю
, то у також має границю 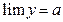 .
.
Цю ознаку іноді називають теоремою про двох міліціонерів.
Ознака 2. Обмежена монотонна змінна величина має границю.
Ця ознака вказує умови, при яких існує границя змінної величини.
Перша ознака вказує не тільки умови існування границі змінної величини, але й величину самої границі.
