Материальные уравнения
Уравнение Максвелла для поля в веществе можно получить из уравнений поля в вакууме. Но их надо рассматривать как обобщения законов сохранения.
пара 
пара 
В этих уравнения появилось два новых вектора 
и 
напряжённость магнитного поля и индукция электрического поля. С помощью этих векторов учитывается вклад заряда вещества в общее поле.
В интегральной форме:
пара 
пара 
Система уравнений (1)-(2) не являются замкнутыми. Это система 8-ми скалярных уравнений относительно 12-ти неизвестных компонент векторов 
.
Поэтому уравнения Максвелла необходимо дополнить соотношениями, которые связывают векторы и , учитывающие вклад заряда в веществе в общее поле, с векторам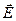и 
и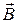 
. Уравнения связи можно записать в виде соотношений: 
(5)
(6)
(7)
Уравнения Максвелла универсальны и пригодны для описания любых сред, в то время как уравнения (5) – (7) существенно зависят от свойства среды, поэтому их называют материальными уравнениями. Эти уравнения могут быть сложными: связь может быть нелинейной, нелокальной во времени и пространстве (т.е. значения 
и 
в некоторые моменты времени и в некоторых точках пространства могут зависеть от 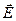и в других точках и в другие моменты времени). Нелокальность уравнений связи обуславливает такие свойства среды, как пространство и временная дисперсия.
В силу линейности уравнений Максвелла их решение удовлетворяют принципу суперпозиции. Для электромагнитного поля в вакууме, например если 
- решения уравнений Максвелла, то и 
,
- тоже решения Максвелла.
Сочетание уравнений Максвелла и линейных уравнений связи составляют основу нелинейной электродинамики.
В простейшем случае матер уравнения имеют вид:
(8)
(9)
(10)
где 
и 
- соотв. диэлектрическую проницаемость, магнитная проницаемость и проводимость среды; в общем случае и - тензоры. Если хотя бы один из и - тензор, то среда анизатропна. В противном случае среда изотропна. Если , зависят (явно) от времени, то среда нестационарна. В противном случае стационарна.
Если , зависят от координат, то среда неоднородна, иначе - однородна.
Для вакуума:
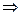
Истинные физические силовые поля (поля, определяющие силу, которая действует на пробный заряд q) характеризуется векторам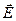и и 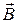. За вектором 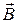сохранилось неудачное название “магнитной индукции”, хотя принято 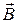является магнитным аналогом напряжённости электрического поля .
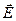