Свойства средней арифметической

Средняя арифметическая величина имеет следующие свойства, использование которых упрощает ее расчет.

1) Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты.

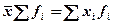
2) Сумма отклонений индивидуального значения признака от средней арифметической равна нулю:

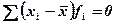
3) Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на туже величину.

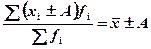
4) Если все варианты значений признака уменьшить или увеличить в А раз, то средняя соответственно уменьшится или увеличится в А раз:

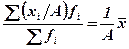
5) Если все частоты уменьшить или увеличить в А раз, то средняя останется неизменной:

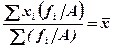
6) Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:

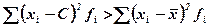
Средние гармонические величины

Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Различают среднюю гармоническую простую и взвешенную.

Средняя гармоническая простая.

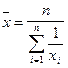
Средняя гармоническая взвешенная применяется тогда, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение.

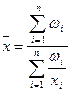
Средняя арифметическая и средняя гармоническая величины могут применятся в одних и тех же ситуациях, но по разным данным. Если в ИСС неизвестен числитель, то в расчетах применяется средняя арифметическая величина. Если в ИСС неизвестен знаменатель, то в расчетах используется средняя гармоническая величина.

Другие виды средних величин

Средняя квадратическая величина применяется тогда, когда вместо индивидуальных значений признака представлены квадраты исходных величин.

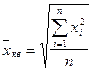
Средняя геометрическаяприменяется в случаях определения средней по значениям, имеющим большой разброс, либо в случаях определения средней величины по относительным показателям.

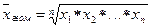
Средняя степенная. В математической статистике различные средние выводятся из формул степенной средней:

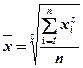
При z = 1 – средняя арифметическая;

z = 0 – средняя геометрическая;

z = –1 – средняя гармоническая;

z = 2 – средняя квадратическая.

Чем выше z, тем больше значения средней величины.

Структурные средние

Характеристиками структуры совокупности являются следующие структурные средние:

1. Мода (Mo) – величина признака, наиболее часто встречающаяся в совокупности, т.е. имеющая наибольшую численность в ряду распределения.

а) В дискретном ряду распределения мода определяется визуально.

б) В интервальном ряду распределения визуально можно определить только интервал, в котором заключена мода, который называется модальным интервалом. Мода будет равна:

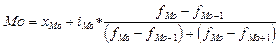
2. Медиана (Me) – значение признака, приходящееся на середину ранжированного ряда, т.е. делящее ряд распределения на две равные части.

а) В дискретном ряду распределения определяется номер медианы по формуле:

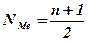
Номер медианы показывает то значение показателя, которое и является медианой.

б) В интервальном ряду распределения медиана рассчитывается по следующей формуле:

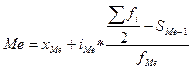
Понятие и меры вариации

Вариации – колеблемость, многообразие, изменяемость величины признака у единиц совокупности.

Измерение вариации позволяет определить степень воздействия на данный признак других варьирующих признаков.

Показатели вариации делятся на абвсолютные и относительные. К абсолютным показателям относятся размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение. К относительным – коэффициенты осцилляции, коэффициенты вариации и относительное линейное отклонение.

Размах вариации – простейший показатель, разность между максимальным и минимальным значениями признака.

Недостатком является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ.

Среднее линейное отклонение отражает все колебания варьирующего признака и представляет собой среднюю арифметическую из абсолютных значений отклонений вариант от средней величины, т.к. сумма отклонений значений признака от средней равно 0, то все отклонения берутся по модулю.

Простая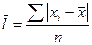

Взвешенная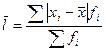

Дисперсия– средний квадрат отклонений значений признака от их средней величины.

Невзвешенная формула: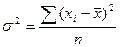

Взвешенная формула: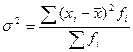

Наиболее удобным и широко распространенным на практике показателем является Среднее квадратическое отклонение. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность, что и изучаемый признак.

Невзвешенная формула: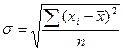

Взвешенная формула: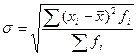

Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемой совокупности. В отличие от них, коэффициент вариации измеряет колеблемость в относительном выражении, относительно среднего уровня, что во многих случаях является предпочтительнее:

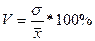
Если коэффициент вариации не превышает 33%, то совокупность по рассматриваемому признаку можно считать однородной.

Относительные показатели.

1) Коэффициент осцилляции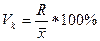

2) Линейный коэффициент вариации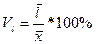

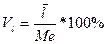
3) Коэффициент вариации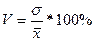

Они определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 %

Свойства дисперсии

1⁰Дисперсия постоянной величины равна 0

2⁰ Уменьшение всех значений признака на одну и ту же величину А не изменяет величину дисперсии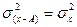

3⁰Уменьшение всех значений признака в В раз уменьшает дисперсию в В² раз, а среднее квадратическое отклонение в В раз

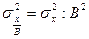
Таким образом все значения признака можно разделить на какую-то постоянную величину, затем определить среднее квабратическое отклонение и умножить его на эту постоянную величину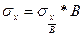

4⁰ Средний квадрат отклонений от любой величины А в той или иной степени отличающейся от средней арифметической всегда будет больше среднего квадрата отклонений, исчисленного от средней арифметической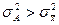

При этом средний квадрат отклонений будет больше на определенную величину (на квадрат разности средней и условно взятой величины)

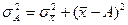
5⁰ Дисперсия имеет свойство минимальности; если А=0, то дисперсия вычисляется по формуле: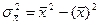

Между средним линейным отклонением и средним квадратическим отклонением существует примерное соотношение. 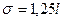в том случае, если фактическое распределение близко к нормальному распределению. Как правило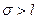

В условиях нормального распределения существует зависимость между величиной среднего квадратического отклонения и количеством наблюдений.

Правило трех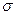

1) В пределах 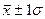располагается 68,3% количества наблюдений

2) В пределах 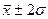находится 95,4% количества наблюдений

3) В пределах 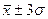находится 99,7% количества наблюдений

Отклонения 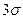считается максимально возможными.