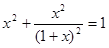В.Метод подбора: при решении уравнений высших степеней рациональные корни уравнения ищем в виде ,где -делитель , - делитель , и взаимно просты
Содержание.
Предисловие.
1. Алгебраические преобразования.
2. Неравенства.
3. Функции и графики.
4. Преобразование степенных и иррациональных выражений.
5. Иррациональные уравнения.
6. Основные методы решения алгебраических уравнений.
7. Уравнения, содержащие модуль.
8. Геометрические задачи.
9. Примерное контрольное задание.
10. Основные формулы.
Литература.
ПРЕДИСЛОВИЕ
Во все времена математика лежала в основе так называемого точного естествознания, была мощным рабочим аппаратом физики, астрономии, техники. Абстрактные математические понятия и теоремы позволяли наиболее полно и точно описывать объективные законы природы.
В последние десятилетия значение математики в общей системе человеческих знаний возросло неизмеримо, ибо усилился интенсивный процесс математизации многих наук. Эти слова следует понимать в том смысле, что только обладая точной математической формой исследования, данная отрасль знаний может получить исчерпывающие количественные результаты. Вот почему математические методы широко применяются в механике, геофизике, геологии, экономике, управлении производством.
На вступительном экзамене надо уметь решать примеры, задачи и при этом решать их правильно, т.е. давать исчерпывающее, логически верное и математически грамотно изложенное решение. Предлагаются не какие-то сложные проблемы, а задачи в пределах обычного школьного курса, которые решаются с помощью изучаемых в школе теорем, правил и приемов.
Как следует выполнять письменную работу по математике на экзамене?
Решение задач, предлагаемых на письменном экзамене должны быть приведены подробно, четко и аккуратно; объяснять выкладки, провести проверку( если это необходимо), указать все ограничения (возникающие как из условия, так и в ходе выкладок): чертежи следует выполнять аккуратно (можно и от руки), все обозначения на чертеже должны быть объяснены и должны совпадать с обозначениями, используемыми в тексте решения.
Поступающие часто допускают в решении арифметические ошибки, путают простейшие формулы. Поэтому следует тщательно контролировать себя, внимательно проверять выкладки.
При выполнении письменной работы полезно учесть несколько «тактических» советов. Целесообразно сначала решать ту задачу, которая кажется более простой, довести ее решение до конца, переписать его начисто, а уже после этого приниматься за решение следующей задачи. Никогда не следует решать одну и ту же задачу несколько часов подряд, если она не получается- в результате может не хватить времени на остальные задачи. Лучше отложить эту задачу и заняться другими, а потом, решив их, вернуться к ней снова. Такая система позволяет наиболее рационально использовать предоставляемое для экзамена время.
На экзамене необходимо проявить определенную выдержку и самообладание , не отвлекаться, не обращаться к справочникам, книгам и т.п.
При подготовке к вступительному экзамену следует обстоятельно изучить материал школьных учебников, всерьез потренироваться в решении примеров и задач.
1. Алгебраические преобразования
Пример: Найти числовые значения выражения:
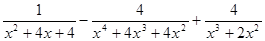 при
при 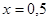 .
.
Решение. 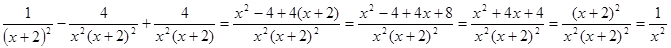 О т в е т: 4.
О т в е т: 4.
Упростить выражение:
1) 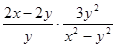 ;
;
2) 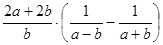 ;
;
3) 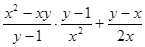 ;
;
4) 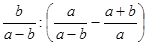 ;
;
5) 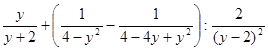 ;
;
6) 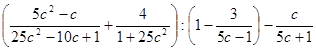 ;
;
7) 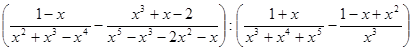 ; Ответ:
; Ответ: 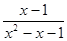 .
.
8) 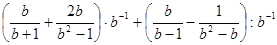 ; Ответ:
; Ответ: 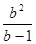 .
.
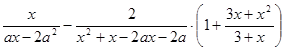 ; Ответ:
; Ответ: 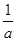 .
.
2. Неравенства
Пример 1: 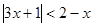 .
.












 Решение.
Решение. 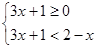 и
и 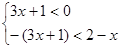
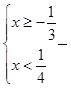 и
и 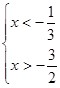
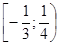
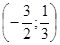
Пример 2: 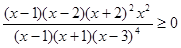 .
.
Решение. 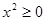 ;
; 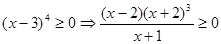
|
 |
|
|
|
-2 -1 0 2 3
О т в е т: 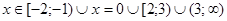 .
.
Решить неравенства.
1) 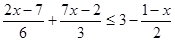 ;
;
2) 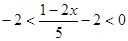 ;
;
3) 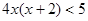 ;
;
4) 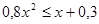 ;
;
5) 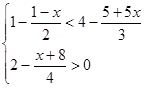 ;
;
6) 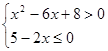 ;
;
7) 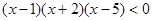 ;
;
8) 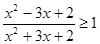 ;
;
Найдите область определения функции:
1) 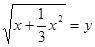 ; 4)
; 4) 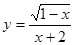 ;
;
2) 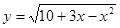 ; 5)
; 5) 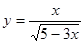 ;
;
3) 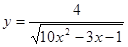 ;
;
3. Функции и графики
Пример: Построить график функции 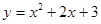 .
.
Решение.
1) Находим координаты вершины параболы 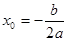 ;
; 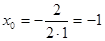 ;
; 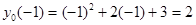 (-1;2)
(-1;2)
2) Точки пересечения параболы с осями координат 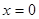 ;
; 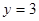
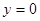
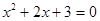
D= 4 – 12= - 8 < 0
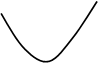
 3) Строим график.
3) Строим график.

 1
1

-1
1) Построить график функции
a) 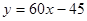
b) 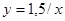
c) 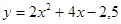
d) 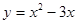
e) 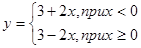
f) 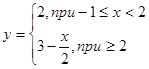
2) Решить графически систему уравнений
a) 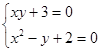 e)
e) 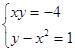
b) 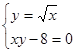 f)
f) 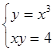
c) 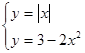 g)
g) 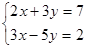
d) 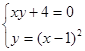 h)
h) 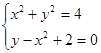
3) Решить графически уравнения:
a) 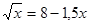 d)
d) 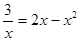
b) 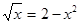 e)
e) 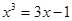
c) 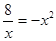 f)
f) 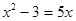
4. Преобразования степенных и иррациональных выражений
Пример 1. Найдите значение выражения 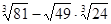 .
.
1) 14 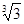 ; 2)
; 2) 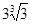 ; 3)
; 3) 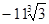 ; 4)-11.
; 4)-11.
Решение. Учитывая, что 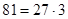 , а
, а 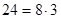 , и используя формулу
, и используя формулу 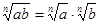 , получим:
, получим:
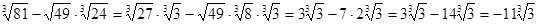 .
.
Такой ответ среди приведенных ответов стоит под номером 3.
О т в е т: 3.
Пример 2. Выполните действия: 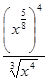 .
.
1) 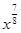 ; 2)
; 2) 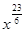 ; 3)
; 3) 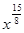 ; 4)
; 4) 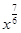 .
.
Решение. 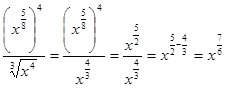 .
.
О т в е т: 4.
Пример 3. Упростите выражение 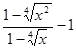 .
.
1) 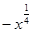 ; 2) 0; 3)
; 2) 0; 3) 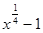 ; 4)
; 4) 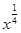 .
.
Решение. Используя определение степени с дробным показателем 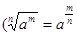 , где
, где 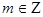 ,
, 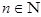 ,
, 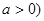 и свойство степени
и свойство степени 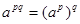 , получаем:
, получаем:
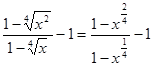 .
.
Обозначив 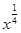 буквой
буквой 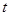 , полученное выражение можно записать так:
, полученное выражение можно записать так: 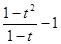 .
.
Разложив числитель на множители, сократим дробь и приведем подобные члены полученного многочлена: 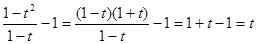 .
.
Следовательно, 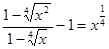 .
.
О т в е т: 4.
Пример 4. Упростите выражение 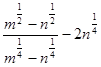 .
.
1) 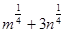 ; 2)
; 2) 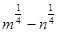 ; 3)
; 3) 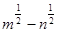 ; 4)
; 4) 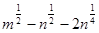 .
.
Решение. 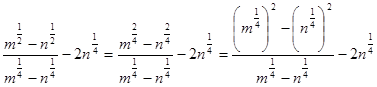 .
.
Пусть 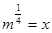 ,
, 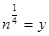 . Далее получаем:
. Далее получаем: 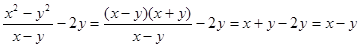 , то есть
, то есть 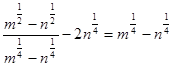 .
.
О т в е т: 2.
Пример 5. Упростите выражение 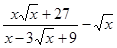 .
.
1) 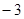 ; 2)
; 2) 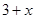 ; 3)
; 3) 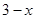 ; 4)
; 4) 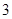 .
.
Решение. Используя определение степени с дробным показателем и свойства степеней, получаем: 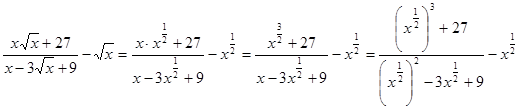 .
.
Пусть 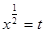 , тогда
, тогда 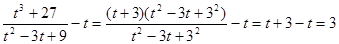 .
.
Итак, 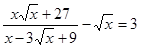 .
.
О т в е т: 4.
Пример 6. Упростите выражение 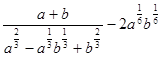 .
.
1) 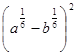 ; 2)
; 2) 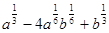 ; 3)
; 3) 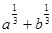 ; 4)
; 4) 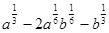 .
.
Решение. 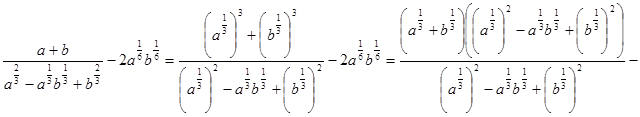
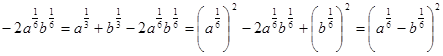 .
.
О т в е т:1
Решите самостоятельно.
1. Упростите выражение 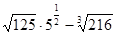 .
.
1) 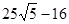 ; 2)
; 2) 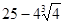 ; 3)19; 4)
; 3)19; 4) 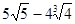 .
.
2.Упростите выражение 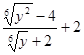 .
.
1) 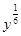 ; 2)
; 2) 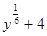 ; 3)
; 3) 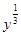 ; 4)
; 4) 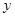 ;
;
3.Упростите выражение 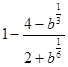 .
.
1) 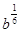 ; 2)
; 2) 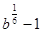 ; 3)
; 3) 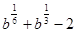 ; 4)
; 4) 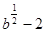 .
.
4.Упростите выражение 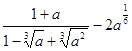 .
.
1) 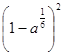 ; 2)
; 2) 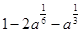 ; 3)
; 3) 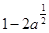 ; 4)
; 4) 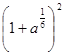 .
.
5.Упростите выражение 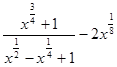 .
.
1) 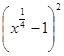 ; 2)
; 2) 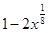 ; 3)
; 3) 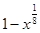 ; 4)
; 4) 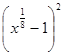 .
.
Иррациональные уравнения.
Пример 1. Укажите промежуток, на котором лежит корень уравнения 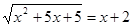 .
.
1) 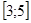 ; 2)
; 2) 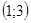 ; 3)
; 3) 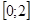 ; 4)
; 4) 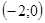 .
.
Решение. Возведем обе части уравнения в квадрат: 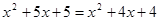 .
.
После преобразований получим 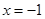 . Проверим, является ли –1 корнем исходного уравнения:
. Проверим, является ли –1 корнем исходного уравнения: 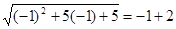 ,
, 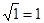 .
.
Последнее равенство верно, следовательно, -1 - искомый корень. Так как 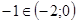 , то верный ответ №4.
, то верный ответ №4.
О т в е т: 4.
Пример 2. Сколько корней имеет уравнение 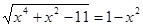 ?
?
1) ни одного; 2) один; 3) два; 4)четыре;
Решение. 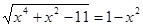 ;
; 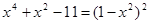 ;
; 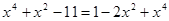 ;
;
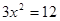 ;
; 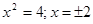 .
.
Проверка. 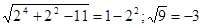 - равенство неверно, значит, 2 – не корень.
- равенство неверно, значит, 2 – не корень.
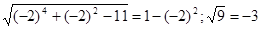 - равенство неверно, значит, -2 – не корень.
- равенство неверно, значит, -2 – не корень.
О т в е т: 1.
Пример 3. Найдите решение системы 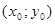 уравнений
уравнений 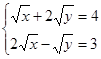 и вычислите значение суммы
и вычислите значение суммы 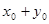 .
.
1) 7; 2) 5; 3) 3; 4) 2.
Решение. Введем обозначения: 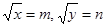 . Получим:
. Получим: 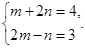
Умножим второе уравнение на 2 и сложим с первым: 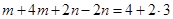 .
.
Отсюда получаем: 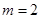 . Подставив 2 в первое уравнение, получим:
. Подставив 2 в первое уравнение, получим: 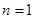 .
.
Итак, 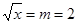 , следовательно,
, следовательно, 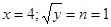 , значит,
, значит, 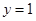 . Итак, пара
. Итак, пара 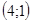 - искомое решение системы уравнений:
- искомое решение системы уравнений: 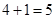 .
.
О т в е т:2.
Решите самостоятельно.
1. Укажите промежуток, которому принадлежит корень уравнения 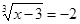 .
.
1) (-6;-3); 2) (-3;0); 3) (0;3); 4) (3;6).
2. Сколько корней имеет уравнение 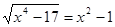 ?
?
1) четыре; 2) два; 3) один; 4) ни одного.
3. Найдите сумму корней уравнения 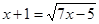 .
.
1) –1; 2) 1; 3) 4; 4) 5.
4. Найдите решение 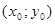 системы уравнений
системы уравнений 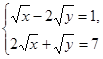 и вычислите значение суммы
и вычислите значение суммы 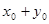 .
.
1) 4; 2) 5; 3) 7; 4) 10.
6. Основные методы решения алгебраических уравнений.
I. Линейные уравнения 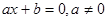 . Такое уравнение имеет один корень, нахождение которого не вызывает затруднений:
. Такое уравнение имеет один корень, нахождение которого не вызывает затруднений: 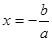 .
.
II. Квадратное уравнение 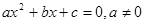 . Квадратные уравнения решаются по готовой формуле
. Квадратные уравнения решаются по готовой формуле 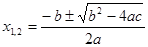 ; используется теорема Виета:
; используется теорема Виета: 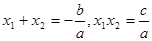 .
.
Пример 1. Решить уравнение 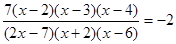 .
.
Решение. Предложенное уравнение не является алгебраическим. Более того, не любые значения неизвестной 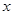 могут выступать в качестве корней этого уравнения. Начинать решение таких уравнений необходимо с указания области определения переменной
могут выступать в качестве корней этого уравнения. Начинать решение таких уравнений необходимо с указания области определения переменной 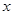 .
.
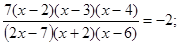
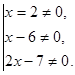 (1)
(1)
Теперь приводим уравнение к виду 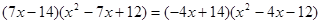 и раскрываем скобки:
и раскрываем скобки: 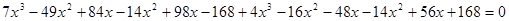 .
.
Приводим подобные слагаемые и получаем:
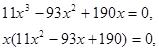
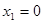 .
. 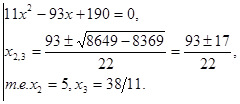
Найденные значения 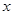 удовлетворяют соотношениям (1).
удовлетворяют соотношениям (1).
О т в е т: 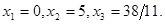
З а д а ч и. Решить уравнения.
1) 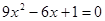
2) 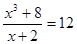
3) 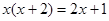
4) 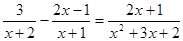
5) 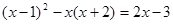
6) 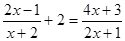
7) 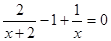
III. Уравнения степени большей чем 2.
А. Метод группировки. Путём группировки слагаемых, применения формул сокращенного умножения привести (если удается) уравнение к виду, когда слева записано произведение нескольких сомножителей, а справа – ноль. Затем приравниваем к нулю каждый из сомножителей.
Пример 2. Найти корни уравнения 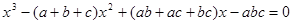 .
.
Решение: 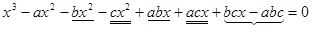 , группируем:
, группируем:
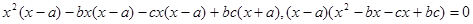 ,
,
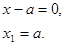
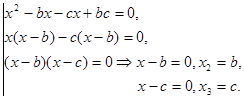
О т в е т: 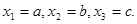
Замечание: корни уравнения можно было легко найти, пользуясь теоремой Виета для кубического уравнения: если 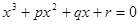 , то
, то
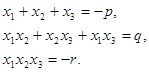
В нашем случае
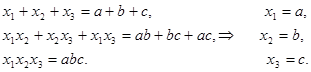
З а д а ч и. Решить уравнения. 
1)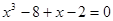
2) 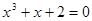
3) 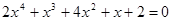 (положить
(положить 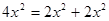 )
)
Б.Метод подстановки. Ищем в уравнении некоторое повторяющееся выражение, которое обозначим новой переменной, тем самым упрощая вид уравнения. В некоторых случаях очевидно что обозначить. Например, уравнение 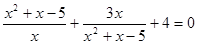 легко решается с помощью подстановки
легко решается с помощью подстановки 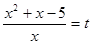 , получаем
, получаем 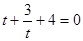 . Или
. Или 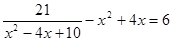 . Здесь можно сделать подстановку
. Здесь можно сделать подстановку 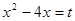 . Тогда
. Тогда 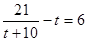 и т.д.
и т.д.
В более сложных случаях подстановка видна лишь после преобразований. Например, дано уравнение 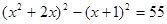 . Переписав его иначе, а именно
. Переписав его иначе, а именно 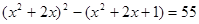 , сразу увидим подстановку
, сразу увидим подстановку 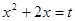 . Имеем
. Имеем 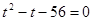 ,
, 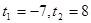 . Осталось решить
. Осталось решить 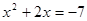 и
и 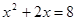 .
.
В ряде других случаев удобную подстановку желательно знать заранее.
Например:
1) Уравнение 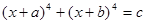 сводится к биквадратному, если сделать подстановку
сводится к биквадратному, если сделать подстановку 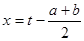 .
.
2) Симметрическое уравнение 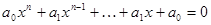 (коэффициенты членов, равноотстоящих от концов, равны) решается с помощью подстановки
(коэффициенты членов, равноотстоящих от концов, равны) решается с помощью подстановки 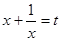 , если
, если 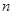 - четное; если
- четное; если 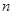 - нечетное, то уравнение имеет корень
- нечетное, то уравнение имеет корень 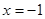 .
.
3) Уравнение вида 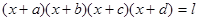 сводится к квадратному, если
сводится к квадратному, если 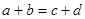 и т.д.
и т.д.
Пример 3. Найти корни уравнения 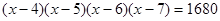 .
.
Решение. Перепишем уравнение в виде 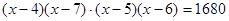 , т.е.
, т.е. 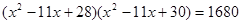 . Обозначим
. Обозначим 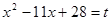 , тогда
, тогда 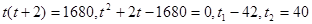 . Поэтому
. Поэтому
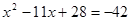 или
или 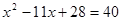

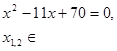
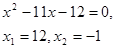
О т в е т: 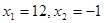 .
.
З а д а ч и.Решить уравнения.
1) 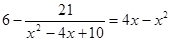
2) 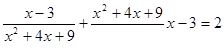
4) 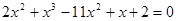
В.Метод подбора: при решении уравнений высших степеней рациональные корни уравнения ищем в виде ,где -делитель , - делитель , и взаимно просты, .
Пример 4. Найти корни уравнения 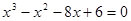 .
.
Решение. Здесь 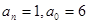 . Поэтому, если данное уравнение имеет рациональные корни, то их следует искать среди делителей числа 6:
. Поэтому, если данное уравнение имеет рациональные корни, то их следует искать среди делителей числа 6: 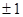 ,
, 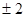 ,
, 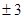 ,
, 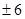 . Проверкой убеждаемся, что
. Проверкой убеждаемся, что 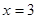 , т.к.
, т.к. 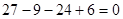 .
.
Делим 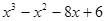 на
на 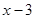 .
.



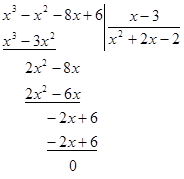
Тогда 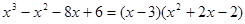 , т.е. данное уравнение можно представить в виде
, т.е. данное уравнение можно представить в виде 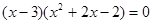 .
.
Отсюда находим, что 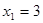 - решение, найденное подбором,
- решение, найденное подбором, 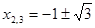 - из уравнения
- из уравнения 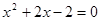 .
.
О т в е т: 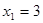 ,
, 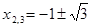 .
.
З а д а ч и.Решить уравнения.
1) 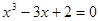
2) 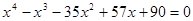
3) 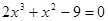
Г.Нестандартный подход. Общих формул нахождения корней алгебраических уравнений высоких степеней нет и поэтому об их решениях говорят как об искусстве решать пример нестандартно, придумать «свой метод», догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д.
Пример 5. Решить уравнение: 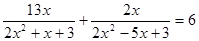 .
.
Решение. Область определения переменной 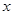 - все действительные числа, кроме корней знаменателей, т.е.
- все действительные числа, кроме корней знаменателей, т.е. 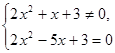 Разделим числитель и знаменатель дробей на
Разделим числитель и знаменатель дробей на 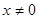 :
: 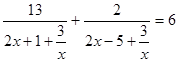 , обозначим
, обозначим 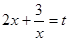 . Получаем
. Получаем 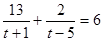 , т.е.
, т.е. 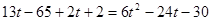 , т.е.
, т.е. 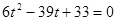 , т.е.
, т.е. 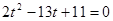 ,
, 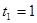 ,
, 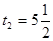 . Следовательно,
. Следовательно, 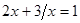 или
или 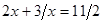

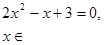
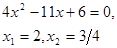
О т в е т: 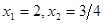 .
.
Пример 6. Решить уравнение: 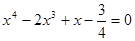 .
.
Решение. Выделим полный квадрат, прибавив и вычтя в левой части уравнения 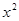 :
: 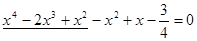 , т.е.
, т.е. 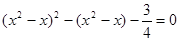 . Пусть
. Пусть 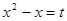 , тогда
, тогда 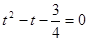 ,
, 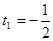 ,
, 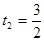 . Возвращаясь к старой переменной, получаем
. Возвращаясь к старой переменной, получаем
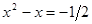 или
или 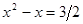

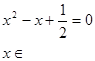
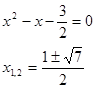
О т в е т: 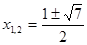 .
.
З а д а ч и.Решить уравнения.
1) 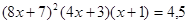
2) 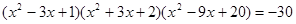
3)