Транспортная задача линейного программирования

4.1. Общая постановка транспортной задачи.

Транспортная задача является одной из важнейших частных задач линейного программирования. Специфические методы ее решения проще общей задачи. Название свое задача получила потому, что впервые была сформулирована и поставлена для решения вопроса о наиболее рациональном планировании перевозок на транспорте. Название это условно, так как с ее помощью можно решать разнообразные задачи из различных отраслей производства и не обязательно связанных с перемещением. Методы решения транспортной задачи широко применяют на автомобильном, железнодорожном и других видах транспорта для планирования перевозок различных грузов. Это объясняется их простотой и экономическим эффектом, который они дают. Планы перевозок, разработанные на основе алгоритма транспортной задачи, как правило, на 12—18% экономичнее планов, составленных без применения математических методов.

В лесной, целлюлозно-бумажной и деревообрабатывающей промышленности транспортирование составляет значительную часть производственного процесса: трелевка древесины, вывозка на промежуточные и нижние склады, доставка па деревообрабатывающие предприятия, междуцеховые и внутрицеховые перемещения на нижних складах и так далее. Транспортные расходы занимают значительный удельный вес в общей структуре лесозаготовок, вот почему задача оптимального планирования работы транспорта является одной из основных задач математического программирования.

Классическая транспортная задача линейного программирования — это задача о наиболее экономичном плане перевозок однородных или взаимозаменяемых грузов из пунктов производства в пункты потребления или, что тоже самое, это задача об оптимальном прикреплении потребителей к поставщикам.

Сформулируем транспортную задачу.

В лесозаготовительном объединении имеются А₁, А₂, ... ..., Аm лесозаготовительных предприятий {ЛЗП), вырабатывающих технологическую щепу в объеме Q₁, Q₂, .... Qm тысяч кубометров в год. Технологическая щепа должна быть доставлена потребителям (ЦБК) В₁, В₂, ….., Вn, имеющим соответственно объемы потребления Y₁, Y₂. … Yn тысяч ку­бометров в год. Стоимость доставки щепы с каждого ЛЗП каждому потребителю определяется матрицей стоимостей:

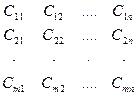(4.1)

Объем выработки щепы всеми ЛЗП равен объему потребления всеми ЦБК:

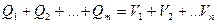(4.2)

или

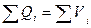(4.3)

Необходимо определить такое распределение доставки щепы от ЛЗП к потребителям, чтобы общая стоимость транспортных затрат была минимальной:

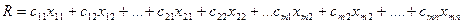(4.4)

или

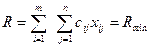(4.5)

При этом необходимо, чтобы соблюдались условия:

1. Суммарный объем щепы, вывозимой с каждого ЛЗП потребителям, должен равняться его мощности:

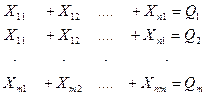(4.6)

или

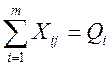(4.7)

где i=1,2,……m.

2. Суммарный объем щепы, доставляемой на каждый ЦБК от ЛЗП, должен равняться его потребности:

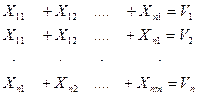(4.8)

или

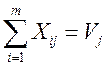(4.9)

где j=1,2,……n.

3.Объемы доставки щепы не могут быть отрицательными, но могут равняться нулю:

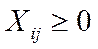(4.10)

4.Уже известное (4.3)

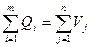
Математически сформулированная транспортная задача ли­нейного программирования:

m+n+2 уравнений,

mxn+1 неизвестных.

Кратко транспортная задача линейного программирования записывается в следующем виде.

Найти минимум функции

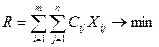(4.11)

При заданных условиях

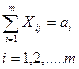(4.12)

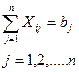(4.13)

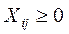(4.14)

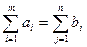(4.15)

Функция 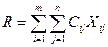называется целевой функцией или

функционалом. Решение задачи сводится к нахождению всех значений X, при которых целевая функция будет минимальной.

4.2. Общий алгоритм решения транспортной задачи

В настоящее время разработано несколько методов (алгоритмов) решения транспортной задачи линейного программирования. Одна группа этих методов основана на принципе последовательного улучшения плана, когда выбранный опре­деленным образом первоначальный план при помощи расчетов улучшается до тех пор, пока не станет оптимальным.

Алгоритм заключается в том, что сначала, строится какой-либо первоначальный допустимый план, затем проверяется, является ли план оптимальным, если план оптимальный — задача решена, если не оптималь­ный— отыскивается другой, но обязательно улучшенный и вновь проверяется на оптимальность. Шаги 2 и 3 повторяются до тех пор, пока очередной улучшенный план не будет оптимальным.

Среди группы методов последовательного улучшения плана можно выделить распределительный метод линейного программирования. Сущность этого метода заключается в том, что на основании известных линейных зависимостей между отдельными факторами составляются матрицы и в результате применения специальных правил подбираются опре­деленные сочетания факторов для получения оптимального решения.

4.3. Методы построения начального плана

Существует несколько методов построения начального плана, который иногда называют опорным решением. Наибо­лее распространенные из них: метод северо-западного угла, метод наименьшей стоимости, двойного предпочтения, по приоритету ближайших пунктов, способ Фогеля, способ Ле­бедева— Тихомирова и др. Рассмотрим простейшие из них.

Метод северо-западного угла, или диагональный, появил­ся одним из первых. Название он получил потому, что рас­пределение поставок (корреспонденции) начинается слева сверху (с северо-западного угла матрицы). Это формальный способ, приводящий к решению обычно далекому от оптимального, но зато простой и легко реализуемый на ЭВМ.

Решение удобно выполнять в табличной форме. Для это­го составляется рабочая таблица в которой в строке слева указываются поставщики (А₁, А₂, ..., Аm) и их мощности, в верхней строке указываются потребители (В₁, В₂, ..., В_n) и их спрос. В клетках таблицы в верхних левых углах указы­ваются единичные стоимости (С₁₁С₁₂ …….. С_mn), т. е. затраты на доставку единицы продукции от соответствующего поставщика А_i (i=1, 2, .... m) соответствующему потребителю B_j (j=1,2,..:,n).

Рассмотрим конкретный пример решения задачи. Три лесозаготовительных предприятия (А₁, A₂, А₃) заготовляют пи­ловочник в объемах соответственно 300, 600 и 500 тыс. м³ в год и поставляют четырем деревообрабатывающим пред­приятиям (В_1, В₂, В₃, В₄). Годовой объем потребления пило­вочника деревообрабатывающими предприятиями равен 450, 400, 200 и 350 тыс. м³. Стоимость доставки сырья от ЛЗП к деревообрабатывающим предприятиям представлена матри­цей стоимостей, показанной в табл. 4.1. цифрами С_ij в левых верхних углах клеток рабочей таблицы.

Таблица 4.1.

Исходные данные для решения транспортной задачи линейного программирования (рабочая таблица).

Поставщики и их мощности, тыс.куб. м.	Потребители и их спрос, тыс.куб.м.
В1	В2	В3	В4
А1
А2
А3

Согласно методу северо-западного угла распределение поставок от поставщиков к потребителям начинается с клет­ки А₁B₁ Сравниваем мощность первого поставщика А₁ (300) с потребностью потребителя B₁ (450). Меньшую величину (300) помещаем в клетку А₁B₁ и вычитаем ее из обеих срав­ниваемых величин. В итоге в остатке первой строки простав­ляется 0, а в итоге первого столбца остаток 450—300=150 (табл.4.2.). Первую строку из дальнейшего рассмотрения исключаем. Поскольку остаток оказался в первом столбце, следующую поставку назначаем в соседнюю клетку А₂B₁. Сравнивая итоги второй строки (600) и первого столбца (остаток 150), устанавливаем величину поставки, равную 150. Вычтя эту поставку из сравниваемых величин, в итоге первого столбца проставляем 0, а в итоге второй строки за­писываем разницу 600—150 = 450. На третьей итерации, срав­нивая потребность потребителя второго столбца B₂=400 и остаток мощности второго поставщика А₂ = 450, меньшее зна­чение записываем в клетку А₂B₂. В остатке второго столбца остается 400—400 = 0, а второй строки 450—400 = 50, что и записываем в остаток по строке в результате третьей итера­ции. Продолжая этот процесс, распределяем поставки по всей таблице. Итог распределения поставок приведен в табл. 4.2.

Таблица 4.2.

Построение опорного плана методом северо-западного угла.

Поставщики и их мощности, тыс.куб. м.	Потребители и их спрос, тыс.куб.м.	Остатки по строкам итерации
В1	В2	В3	В4
А1
А2
А3
Остатки по столбцам	Итерации

В итоге получили некоторое возможное решение. Проверка сумм ∑X_ij по строкам и столбцам показывает на допу­стимость такого плана распределения поставок и отсутствие арифметических ошибок.

Вычислим значение целевой функции. Для этого перемножим удельные стоимости доставки на соответствующие объемы и найдем сумму

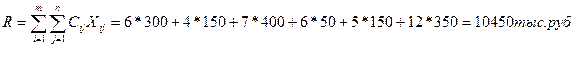
Рассмотрим еще один способ составления начального плана - способ минимального элемента.

Способ минимального элемента несколько сложнее, но позволяет отыскать начальное решение очень близкое к оптимальному, а иногда и оптимальное.

Сущность его заключается в следующем.

В матрице стоимостей отыскивается клетка с минималь­ным значением C_ij и в эту клетку записывается поставка X_ij =min (a_i b_j). Если матрица содержит несколько одинако­вых минимальных значений C_ij, то выбирают любое одно.

После этого вычеркивается строка или столбец. Если a_i> b_j, вычеркивают столбец, при a_i < b_j вычеркивают стро­ку.

Далее процесс (итерации, шаги) повторяют до тех пор, пока не будут распределены все поставки.

Если матрица большая и в уме не удержать нераспреде­ленные мощности и спрос на шагах в процессе распределе­ния на части значений a_i и b_j, в конце каждого шага оста­точные величины записывают.

Рабочая таблица имеет форму, приведенную в табл. 4.3.

Таблица 4.3.

Построение опорного плана по методу минимального элемента.

Поставщики и их мощности, тыс.куб. м.

Потребители и их спрос, тыс.куб.м.

Нераспределенные мощности на шагах

В1

В2

В3

В4

А1

А2

А3

Неудовлетворенный спрос на шагах

Распределение поставок по методу минимального эле­мента выполняется в следующей последовательности.

Шаг 1. Находим минимальное значение стоимости C_ij. В нашем случае это будет C₂₁ = 4. В эту клетку таблицы за­писываем возможную поставку, т. е. минимальную из А₂ и В₁, Сравнивая А₂ = 600 и В₁ = 450, записываем в клетку Х₂₁ поставку 450. Вычисляем нераспределенные мощности по­ставщиков и неудовлетворенный спрос потребителей.

Потребитель В₁ — удовлетворен полностью, во вспомога­тельной части таблицы проставляем 0, а столбец в дальней­ших расчетах не рассматриваем.

Потребитель В₂ неудовлетворен, его спрос остался рав­ным 400, что и записываем во вспомогательной части табли­цы.

Потребитель В₃ — неудовлетворен, спрос остался — 200.

Потребитель В₄ — неудовлетворен, спрос —350.

Поставщик А₁ — мощность его не распределена, остаток нераспределенной мощности, равный 300, записываем во вспомогательной части таблицы справа.

Поставщик А₂ — часть мощности распределена потреби­телю В₁ но осталась нераспределенной мощность 600—450 = = 150, что и записываем во вспомогательную часть таблицы, как нераспределенную мощность на первом шаге.

Поставщик А₃ — мощность его не распределена и запи­сываем результат нераспределенной мощности 500.

Сумма нераспределенных мощностей и неудовлетворен­ного спроса по результатам первой итерации (шага) равна 950, что и записываем в итоге и это является проверкой того, что нет арифметических ошибок.

Шаг 2. Находим минимальное значение стоимости C_ij без вычеркнутого столбца В₁ это значение С₃₃ =5. Записы­ваем в эту клетку возможную поставку-минимум из А₃ = 500 и В₃=200, min=200, записываем нераспределенные мощно­сти и неудовлетворенный спрос на этом шаге и их сумму, равную 750, и вычеркиваем из дальнейшего рассмотрения столбец у которого спрос удовлетворен.

Шаг 3. Минимальный элемент А₂В₂ = 7. В эту клетку записываем минимальное значение из нераспределенной мощ­ности А₂=150 и спроса В₂=400, min=150. В результате третьего шага мощность поставщика А₂ исчерпана, а сумма нераспределенных мощностей и неудовлетворенного спроса осталась равной 600. Продолжая аналогично, доводим рас­пределение до конца,

Шаг 4. Минимальное C_ij из оставшихся имеют клетки А₁В₂ и А₃В₂ — выбираем А₃В_2. Записываем сюда поставку 250 как минимум из значений остатка потребителя В₂ и по­ставщика А₃ и так далее.

Результат распределения по методу минимального элемента показан в табл. 4.3.

Вычисляем значение целевой функции полученного начального решения:

R= 10* 300 + 4 *450 + 7 *150 + 8 *250 + 5*200+ 12*50 = 9450 тыс. руб.

Видим, что это решение более целесообразное, чем полученное методом северо-западного угла. Но это не значит, что полученное решение оптимальное.