Определение и свойства логарифмов
| Формула | Примеры |
1) lоgаb = х, означает ах = b (а > 0, а 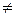 1), т. е. 1), т. е. 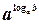 = b основное логарифмическое тождество = b основное логарифмическое тождество | 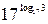 = 3 = 3 |
| 2) lоgаа = 1, (а > 0) | lоg143143 = 1, |
3) lоgр1=0, (р > 0, р 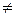 1) 1) | 1оg471=0 |
4) lоg раb = lоgр а + 1оgр b (р > 0, р 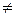 1, а > 0, b > 0) 1, а > 0, b > 0) | log14 2 + log147 = log14 (2 ·7) = 1оg1414 = 1 |
5) lоgр 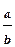 = lоgр а - 1оgр b = lоgр а - 1оgр b | log3 75 — log3 25 = log3 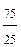 = log3 3 = 1 = log3 3 = 1 |
6) lоg раn = n lоg ра (а > 0, р > 0, р 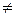 1) 1) | log3 243 = log3 35 = 5log3 3 = 5 |
7) lоg ра = 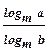 (а > 0, р > 0, р (а > 0, р > 0, р 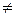 1, m > 0, m 1, m > 0, m 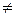 1) 1) |  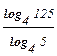 = log5 125 = log5 53 = 3lоg5 5 = 3 = log5 125 = log5 53 = 3lоg5 5 = 3 |
| 8) log10 а = lg а (а> 0) loge а = ln а (а >0) | lg 1000 = log10 1000 = log10 103 = 3 1n е-5 = loge е-5 = - 5 loge е = -5 |
Преобразования логарифмических выражений
Пример 1. Найдите значение выражения 5 ∙ 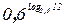
Решение. В соответствии с основным логарифмическим тождеством 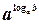 = b получаем:
= b получаем:
5 ∙ 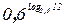 = 5·12 = 60.
= 5·12 = 60.
Ответ: 60
Пример 2. Упростите выражение log3 15 - 1оg35 + 3 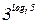
Решение. Используя формулу ) lоgр а - 1оgр b = lоgр 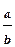 , основное логарифмическое тождество
, основное логарифмическое тождество 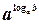 = b, а затем равенство lоgаа = 1, получаем:
= b, а затем равенство lоgаа = 1, получаем:
log3 15 - 1оg35 + 3 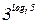 = lоg33 + 5 = 1 + 5 = 6.
= lоg33 + 5 = 1 + 5 = 6.
Ответ: 3.
Пример 3. Вычислите: lоg336 - 21оg32.
Решение. Первый способ.
lоg336 - 21оg32 = lоg3(32 ∙22) - 2lоg32 = lоg332 + lоg322 - 2lоg32 = 2lоg33 + 2lоg32 - 2lоg32 = =2·1 = 2
Второй сgособ.
lоg336 - 21оg32 = lоg336 - 1оg322 = lоg3 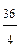 = lоg3 9 = 2
= lоg3 9 = 2 
Ответ:2.
Пример 4. Найдите 1оg 0,3 7,5, если 1оg 0,3 5 = а.
Решение. Представим число 7,5 как произведение степеней с основаниями 5 и 0,3:
7,5 = 25 ·0,3 = 52 ∙0,3 Найдем 1оg 0,3 7,5, используя свойства логарифмов
1оg 0,3 7,5 = 1оg 0,3 (52 ∙0,3) = 1оg 0,3 52 +1оg 0,3 0,3 = 21оg 0,3 5 + 1 = 2а + 1
Ответ: 2а + 1.
Логарифмические уравнения
Пример 1. Найдите произведение корней уравнения 1оg π(х2 + 0,1) = 0.
Решение. По определению логарифма получаем х2 + 0,1 = π0, т. е. х2+0,1 = 1, откуда х2 = 0,9.
Итак, х 1,2 = ± 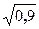 , х1 ·х2 = -
, х1 ·х2 = - 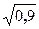 ∙
∙ 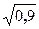 = - 0,9.
= - 0,9.
Ответ: - 0,9.
Пример 2. Какому промежутку принадлежит корень уравнения !оg5(2х) = lоg536 — 1оg54?
1) [0; 4]; 2) (4; 10); 3) [10; 18]; 4) (18; 24).
Решение. Используя свойство логарифмов, Получаем: lоg5(2х) = lоg5 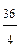 , или lоg5(2х) = 1оg59. Полученное уравнение равносильно уравнению 2х = 9, следовательно, х = 4,5. Т. к.
, или lоg5(2х) = 1оg59. Полученное уравнение равносильно уравнению 2х = 9, следовательно, х = 4,5. Т. к.
4,5 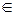 (4; 10), верный ответ №2
(4; 10), верный ответ №2
Ответ: 2.
Пример 3. Укажите промежуток, которому принадлежит корень уравнения
1оg 0,4(5 - 2х) - 1оg 0,4 2 = 1.
1) (- 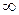 ; -2); 2) [-2; 1]; 3) [1; 2]; 4) (2; +
; -2); 2) [-2; 1]; 3) [1; 2]; 4) (2; + 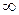 ).
).
Решение. 1оg 0,4(5 - 2х) - 1оg 0,4 2 = lоg 0,4 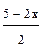 т. к. lоg 0,4
т. к. lоg 0,4 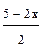 =1, то
=1, то 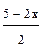 = 0,4
= 0,4
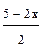 =
= 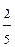 ; 25-10х = 4; -10х = - 21 х = 2,1
; 25-10х = 4; -10х = - 21 х = 2,1
Ответ: 4.
Пример 4. Найдите сумму корней уравнения lg(4х — 3) = 2lgх.
Решение. Уравнение lg(4х — 3) = 2lgх равносильно системе
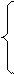 |
4х - 3 = х2,
х> 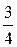 .
.
4х - 3 = х2 х2 - 4х + 3 = 0; х1 = 1, х2 = 3; 1 > 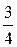 , 3 >
, 3 > 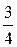 , значит, числа 1 и 3 — корни исходного уравнения; 1 + 3 = 4.
, значит, числа 1 и 3 — корни исходного уравнения; 1 + 3 = 4.
Ответ: 4.
Показательные уравнения
Пример 1. Укажите промежуток, которому принадлежит корень уравнения 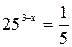
1) (0; 1); 2)(1;2); 3) (2; 3); 4) (3; 4).
Решение. Используя свойство степени (ах)у = аху, получаем:
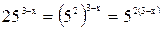
Так как 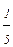 = 5-1, то 52(З-х) = 5-1 Степени с одинаковым основанием равны, значит, равны их показатели: 2(3 - х) = -1; 6 - 2х = -1, - 2х = -7, х = 3,5
= 5-1, то 52(З-х) = 5-1 Степени с одинаковым основанием равны, значит, равны их показатели: 2(3 - х) = -1; 6 - 2х = -1, - 2х = -7, х = 3,5
Поскольку 3,5 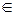 (3; 4), верным является ответ №4.
(3; 4), верным является ответ №4.
Ответ: 4.
Пример 2. Укажите промежуток, которому принадлежит корень уравнения
2 х-1 + 2 х+1 = 20.
1) (4; 5); 2) [3; 4]; 3) (2; 3); 4) [1; 2].
Решение. 2 х-1 + 2 х+1 = 20; 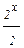 + 2·2х = 20; 2х + 4∙2х = 40; 5 ·2х = 40; 2х = 8; х = 3;
+ 2·2х = 20; 2х + 4∙2х = 40; 5 ·2х = 40; 2х = 8; х = 3;
х 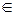 [3;4].
[3;4].
Ответ: 2.
Пример 3. Найдите произведение корней уравнения 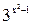 = 243.
= 243.
Решение. 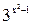 = 243;
= 243; 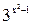 = 35; х 2 - 1 = 5;
= 35; х 2 - 1 = 5;
| Первый способ | Второй способ |
х2=6; х1,2= 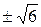 х1·х2 = х1·х2 = 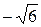 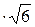 = -6 = -6 | х2 – 6 = 0 х1·х2 = -6 (по теореме Виета) |
Ответ: 1
Формулы дифференцирования основных функций (Производные).
1) (хm)´ = m хm-1 2) ( 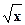 )´ = )´ = 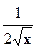 3) 3) 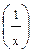 ´ = ´ = 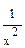 4) (ех)´ = ех 5) (ах)´ = ах1nа 6) (lnx)´ = 4) (ех)´ = ех 5) (ах)´ = ах1nа 6) (lnx)´ = 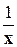 7) (lоgх)´ = 7) (lоgх)´ = 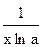 | 8) (sin x)´ = cos x 9) (cos x)´ = - sin x 10) (tg x)´ = sес2 х = 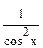 11) (ctg x)´ = - cоsес2х = 11) (ctg x)´ = - cоsес2х = 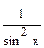 12) (arcsin x)´ = 12) (arcsin x)´ = 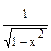 13) (агссоs х)´ = - 13) (агссоs х)´ = - 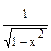 |
