Затухающие колебания

Дифференциальное уравнение затухающего колебания. Уравнение для смещения. Коэффициент затухания. Логарифмический декремент затухания.

Колебания, происходящие в системе при отсутствии внешних сил (но при наличии потерь на трение или излучение), называются свободными. Частота свободных колебаний зависит от свойств системы и интенсивности потерь.

Наличие трения приводит к затухающим колебаниям. Колебания с убывающей амплитудой называются затухающими.

Допустим, что на систему, кроме квазиупругой силы, действуют силы сопротивления среды (трения), тогда второй закон Ньютона имеет вид:

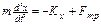
Ограничимся рассмотрением малых колебаний, тогда и скорость системы будет малой, а при небольших скоростях сила сопротивления пропорциональна величине скорости:

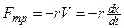(2)

где r - коэффициент сопротивления среды. Знак "-" обусловлен тем, что F_тр и V имеют противоположные направления. Подставим (2) в (1). Тогда

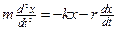или 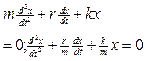Обозначим 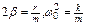, где b - коэффициент затухания, w₀ - круговая частота собственных колебаний. Тогда

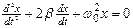(3)

Решение этого уравнения существенно зависит от знака разности:

w² =w₀² -b²

где w - круговая частота затухающих колебаний. При условии w₀² - b²> 0

w является действительной величиной и решение (3) будет следующим:

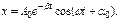
График этой функции дан на рисунке.

Пунктиром изображено изменение амплитуды: A = ± A₀ e^-bt

Период затухающих колебаний зависит от коэффициента трения и равен 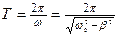(4)

При незначительном сопротивлении среды ( b² << w² ) период практически равен 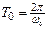. С ростом коэффициента затухания период колебаний увеличивается.

Из формулы, выражающей закон убывания амплитуды колебаний, можно убедиться, что отношение амплитуд, отделенных друг от друга интервалом в один период (Т), остается постоянным в течение всего процесса затухания. Действительно, амплитуды колебаний, отделенных интервалом в один период выражаются так:

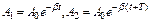
Отношение этих амплитуд равно:

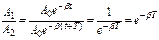
Это отношение называютдекрементом затухания.

В качестве меры затухания часто берут величину натурального логарифма этого отношения:

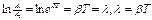
Эта величина носит название логарифмического декремента затухания за период.

При сильном затухании b² > w₀² из формулы (4) следует, что период колебания является мнимой величиной. Движение при этом носит апериодический (непериодический) характер - выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний. На рисунке показано два возможных способа возвращения системы к положению равновесия при апериодическом движении.

Каким из этих способов приходит система в положение равновесия, зависит от начальных условий.

Вынужденные колебания. Резонанс.

Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы (вынуждающей силы). Пусть вынуждающая сила изменяется со временем по гармоническому закону: f = F₀ cosW t ,

где F₀ - амплитуда, W - круговая частота вынуждающей силы.

При составлении уравнения движения нужно учесть, кроме вынуждающей силы, также те силы, которые действуют в системе при свободных колебаниях, то есть квазиупругую силу и силу сопротивления среды. Тогда уравнение движения (второй закон Ньютона) запишется следующим образом:

.

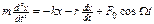Разделив это уравнение на m и перенеся члены с dx и d²x в левую часть получим неоднородное линейное дифференциальное уравнение второго порядка:

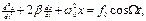
где 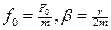- коэффициент затухания, 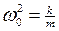- собственная частота колебаний системы. Решением этого уравнения будет: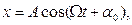

где 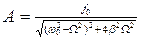(1)

Явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте колеблющегося тела называется резонансом, происходящие при этом колебания - резонансными, а их частота w _рез - резонансной частотой колебаний.

Расчет дает значение резонансной частоты:

w_рез =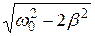

Если b очень мало, то w_p » w₀ . Подставив w_рез вместо W в (1), получим максимальную величину амплитуды колебаний при резонансе:

А_рез = .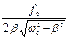

Чтобы определить резонансную частоту w_рез , нужно найти максимум функции (1) или, что то же самое, минимум выражения, стоящего под корнем в знаменателе. Продифференцировав это выражение по W и приравняв нулю, мы получим условие, определяющее w_рез :

-4(w₀² -W²) W + 8b² W = 0.

Это уравнение имеет три решения: W = 0 и .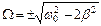

Решение, равное нулю, соответствует максимуму знаменателя. Из остальных двух решений отрицательное должно быть отброшено, как не имеющее физического смысла (частота не может быть отрицательной). Таким образом, для резонансной частоты получается одно значение: w_рез = 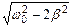.Подставив это значение частоты в (1), получим выражение для амплитуды при резонансе :

а_рез =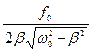

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы (частоты колебаний) показана графически на рисунке:

b₁ < b₂ <b₃

Это резонансные кривые.