Лекция 6 термическое и электродинамическое действие токов короткого замыкания

В режиме короткого замыкания токоведущие элементы электри­ческой установки (шины, кабели и др.) за небольшое время короткого замыкания t (секунды или доли секунды) нагреваются током к. з. от не­которой начальной температуры θ_н до температуры θ _макс. Токи к. з. во мно­го раз больше токов нормального ре­жима, поэтому, несмотря на малую продолжительность короткого замы­кания, температура проводников рез­ко возрастает и θ_макс становится много больше θ_Н (рис. 6.1).Опреде­ление температуры θ_макс и сравне­ние ее с кратковременно допустимой θ_{макс доп} является задачей тепловых расчетов для режима к. з.

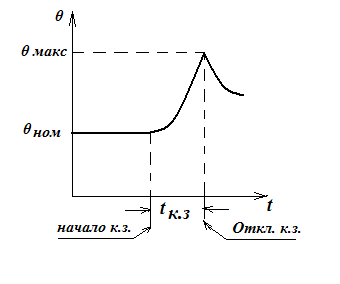
Рис.6.1 Нагрев проводника в режиме короткого замыкания

Небольшое время t короткого за­мыкания позволяет производить тепловые расчеты при к. з. без уче­та отдачи тепла в окружающую среду за это время. Рассмотрим нагрев проводника периодической составляющей тока к. з., оставив пока в стороне дополнительный нагрев его аперио­дической составляющей тока к. з. Такое раздельное рассмотрение двух составляющих тока к. з. возможно, что непосредственно следует из выражения для действующего тока короткого замыкания I_к.з. :

I²_к.з = I²_пt + I²_at (6.1)

где I_at - значение апериодической составляющей, а I_пt – периодической составляющей.

Энергия, затраченная на нагрев проводника током t _пt , выражается законом Ленца. Тогда исходное выражение нагрева проводника выглядит как:

i²_пt R_np t = C m θ (6.2)

где R_np – сопротивление проводника, С –удельная теплоемкость материала проводника, m – вес проводника.

Ввиду того , что ток изменяется в течении времени к.з. а теплоемкость и сопротивление проводника являются функцией температуры, исходное уравнение нагрева является дифференциальным:

i²_пt ρ_о ( 1+ αθ) dt = slγc_o ( 1+ β θ)d θ (6.3)

где i_пt – мгновенное значение периодической составляющей к.з.

ρ_о ( 1+ αθ) - сопротивление проводника при температуре θ^оС, ом

c_o ( 1+ β θ) -удельная теплоемкость материала проводника при θ^оС, вт^. с / г^{. о}С

ρ_о и c_o – удельные сопротивление и теплоемкость при 0^оС

α и β температурные коэффициенты изменения ρ и c

sl – объем проводника, см³; γ – уд. вес материала проводника, г/см³

Разделив переменные и перегруппировав коэффициенты, перепишем уравнение в следующем виде:

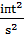dt = к 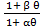d θ (6.4)

где к = γ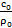

За время короткого замыкания t температура проводника поднимается от начального значения θ_н до θ_мах конечного значения, потому следует проинтегрировать обе части уравнения в указанных пределах:

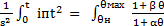d θ ( 6.5)

Закон изменения величины i_пt во времени достаточно сложен, поэтому интегрирование этой функции производят заменой площадей (интегралов). Рис.6.2. иллюстрирует этот метод.∞

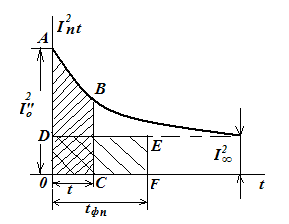
Рис.6.2 График определения фиктивного времени периодической составляющей.

На графике рис.6.2 площадь ОАВС, соответствующая времени к.з. t равна теплу от тока к.з. за время t, т.е.

пл.ОАВС = 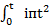dt

Такое же количество тепла мог выделить установивщийся (неизменный) ток к.з. I²∞ но уже за другое время t_фп. Это время можно найти, построив равновеликий по площади прямоугольник ODEF. Для определения t_фп при известном времени t по расчетным кривым токов к.з. построена зависимость t_фп=f (λ) (рис.6.3), причем λ = I” / I∞. Таким образом можно вычислить интеграл как:

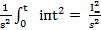t_фп (6.6)

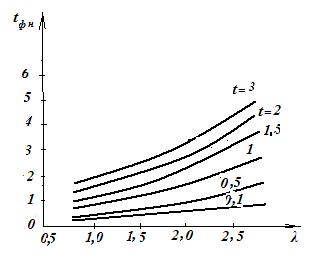
Рис.6.3 Кривые для определения фиктивного времени

Тепло, выделяемое апериодической составляющей тока к.з. i_аt определяется уравнением аналогично уравнению 6.6:

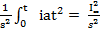t_ф.а. (6.7)

где t_ф.а. – время, за которое установившийся ток к.з. выделит то же количество тепла, что и апериодическая составляющая тока к.з. за время короткого замыкания t.

Апериодическая составляющая затухает с постоянной времени цепи до точки к.з. Т_а : i_аt =√2I^”_o е ^-t/Ta (6.8)

где I^”_o – известное ( уравнение 5.9) действующее значение сверхпереходной составляющей тока к.з. в момент времени равном 0. Эта функция легко интегрируется и в результате значение фиктивного времени апериодической составляющей:

t_ф.а = Т_аλ², (6.9)

где λ = I^”_o/

Полное фиктивное время t_ф = t_фп + t_ф.а

Интегрирование правой части уравнения 6.5 сложно и приводит к громоздкому выражению для определения искомой температуры θ_мах. На основании этого выражения построены расчетные кривые в предположении, что начальная температура проводника θ_н =0. Порядок пользования кривыми вытекает из их построения. Сперва находят начальную температуру проводника к моменту к.з. θ_н. :

θ_{н =} θ_среды + (θ_доп - θ_среды) I² _раб / I² _доп (6.10)

где θ_среды – расчетная температура среды

θ_доп – длительно допустимая температура проводника

I _раб – рабочий ток через проводник

I _доп – допустимый ток через проводник

Значения θ_доп приведены в справочных таблицах выбора шин и кабелей. За θ_среды принимают максимально возможную при эксплуатации ( например +40^оС ). Определив начальную температуру находят по кривым (рис 6.4) значение соответствующей ей абсциссы а_н. Затем подсчитывают t_ф и определяют абсциссу а_к = а_н + t_ф. Значение θ_мах определяют по значению а_к. Далее величину θ_мах сопоставляют с θ_{махдоп.} для данного вида материала проводника.

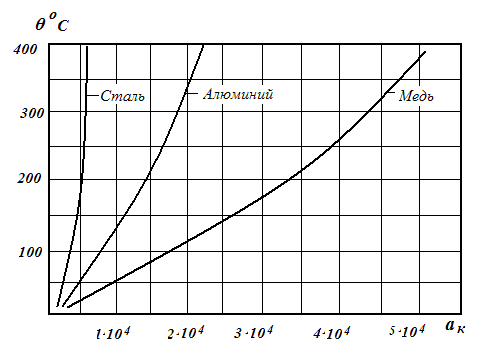
Рис.6.4 Кривые для определения температуры нагрева проводников при коротких замыканиях.

В связи с тем, что продолжительность короткого замыкания мала ( не превышает нескольких секунд), за θ_махдоп принимают температуры, значительно большие, чем допустимые температуры при длительном нагреве. При этом учитывается, что изоляция проводников способна выдержать θ_махдоп без ущерба для дальнейшей работе.

Для голых проводников ( шин распредустройств) θ_махдоп принимают из условий механической прочности материала. Например, для голых медных шин θ_махдоп = 300^оС.

Токопроводы, защищаемые предохранителями можно не проверять на термическую устойчивость, также как и токопроводы, защищаемые токоограничивающими выключателями и выключателями, без специально вводимой выдержки времени при срабатывании.

Селективные автоматы ( автоматы с настраиваемо выдержкой времени при отключении к.з.) на термическую стойкость проверяют по условию

I ² _¥ t _ф < (I ² t ) _доп.,

где I _¥ - установившийся ток к.з.; t _ф – фиктивное время к.з.;

(I ² t ) _доп. – термическая устойчивость по техническим условиям (справочные данные).

ЭЛЕКТРОДИНАМИЧЕСКОЕ ДЕЙСТВИЕ ТОКА К,З,

При протекании тока i в контуре в последнем возникает электродинамическая сила F, стремящаяся деформировать контур (рис.6.5). При постоянном значении тока приращение энергии поля W при деформации контура в направлении х равно работе, совершенной электромагнитной силой F за тот же промежуток времени.

dW = Fdx (6.11)

где х - координата направления силы.

Уравнение 6.11 называется уравнением Максвелла.

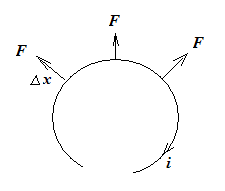
Рис. 6.5 Действие электродинамических сил на контур с током.

Магнитная энергия W в контуре с индуктивностью L и током i определяется известным выражением:

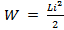(6.12)

Тогда

F = 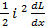(6.13)

При двух контурах с индуктивностями L₁ и L₂ и соответственно токами i₁ и i₂ и взаимной индуктивностью М энергия магнитного поля W определяется выражением:

W = L₁ i²₁ + L₂ i²₂ + М i₁ i₂ (6.14)

Электродинамическая сила, стремящаяся изменить взаимное расположение жестких контуров (L₁=const; L₂=const) равна:

F = i₁ i₂ 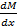(6.15)

Взаимная индуктивность (Гн) двух параллельных проводников, расположенных в одной плоскости на расстоянии много меньшем, чем их длина.

М= 2l( ln 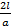-1)10^-7 Гн (6.16)

Тогда

dM /dx = dM/da = (2l / a)10^-7 (6.17)

и F = (2i₁i₂ l / a) 10^-7 Н (6.18)

Этой формулой пользуются для определения силы взаимодействия между шинами распределительных устройств при прохождении токов короткого замыкания.

При расчетах механической прочности шин в режиме короткого замыкания исходят из допущения, что шина каждой фазы является многопролетной балкой, свободно лежащей на жестких опорах и на­ходящейся под действием равномерно распределенной нагрузки. Шины распределительного щита. удовлетворяют требованиям электродинамической устойчивости, если значение максимального расчетного на­пряжения в шине меньше или равно максимально допустимого напряжения, т.е. σ_расч. ≤ σ_доп

В случае невыполнения этого неравенства рекомендуется уменьшить σ_расч. путем проведения ряда мероприятий:

а) уменьшения величины тока короткого замыкания ;

б) увеличения расстояния между осями шин ;

в) уменьшения длины пролета между опорными изоляторами ;

г) изменения размера сечения шин.

Максимальное напряжение в шине при расположении шин плашмя определяется по соотношениям:

При числе пролетов больше двух

σ_расч. = (1.06 К_ф i ²_р L²/ a h² b) * 10 ^-10 , кПа (6.19. )

при числе пролетов, равном двум

σ_расч. = (1.33 К_ф i ²_р L²/ a h² b) * 10 ^-10 , кПа (6.20)

При расположении шин согласно рис .6.6 а. максимальное напряжение

в шине равно: .

σ_расч. = (1.06 К_ф i ²_р L²/ a h b²) * 10 ^-10 , кПа (6.21)

при числе пролетов, равном двум,

σ_расч. = (1.33 К_ф i ²_р L²/ a h b²) * 10 ^-10 , кПа (6.22)

где i _р - полный ударный ток короткого замыкания ;

а - расстояние между осями фаз, см, обычно а = 6…...7 см

L - длина пролета, см, обычно L = 60 см;

h- высота шин, см ;

б - толщина шин, см ;

К_ф - коэффициент формы шин, определяемый из кривых, представленных на рис.6.7

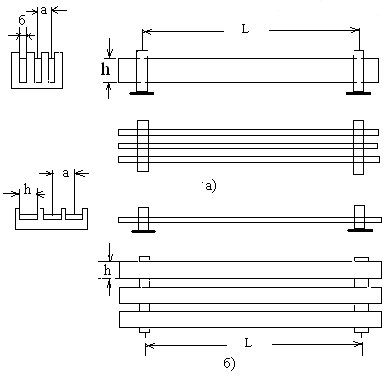
Рис. 6.6 Расположение однопролетных шин

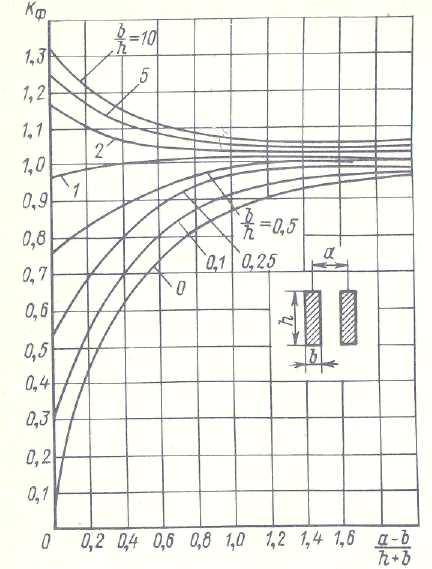
Рис. 6.7 Зависимость коэффициента формы шин от взаимного расположения и конфигурации.

Автоматические выключатели проверяют на электродинамическую устойчивость по ударному току к.з. до отключения выключателя. Селективные (генераторные) автоматы кроме динамической стойкости проверяют и на предельную отключающую способность.

Предельная отключающая способность определяется допустимой величиной тока в момент расхождения контактов. Условие проверки на динамическую стойкость:

i _{уд. расч.} < i _{уд. доп.} ;

на разрывную способность:

I_{t расч.} < I_{t доп},

где i _{уд. расч.} – расчетный ударный ток к.з. для точки, выбранной с целью проверки автомата; i _{уд. доп.} – допустимое значение ударного тока к.з. автомата; I_{t расч} – расчетное действующее значение тока к.з. в момент расхождения дугогасительных контактов ( соответствующее уставке по времени); I_{t доп}, - допустимое действующее значение тока выключателя в момент расхождения дугогасительных контактов.

Контрольные вопросы.

1. Почему токопроводы, защищаемые предохранителями можно не проверять на термическую устойчивость?

2. Как выразить энергию, затрачиваемую на нагрев проводника током?

3. Почему при расчете этой энергии приходится вводить «фиктивное» время?

4. Какие условия предлагаются для проверки селективных автоматов на термическую стойкость и на разрывную способность?

5. От каких конструктивных параметров зависит максимальное механическое напряжение шины?

6. Какие мероприятия следует провести для уменьшения электродинамического воздействия на однополосные шины?