Основные правила и формулы алгебры событий

С алгеброй чисел (букв) мы знакомы из средней школы. Назовем эту алгебру обыкновенной и заметим, что есть много прикладных задач математики, которые нельзя решить в рамках обыкновенной алгебры. Значит, нужен новый математический аппарат. Таким аппаратом является необыкновенная алгебра- алгебра Буля.

Джордж Буль (1815-1864)-английский математик (отец писательницы Э.Войнич автора романа «Овод»). Д.Буль был выходцем из семьи ремесленника, математикой овладел путем самообразования. Будучи не связанным, традициями математики высшей школы он создал свою необыкновенную алгебру, которая позволила найти решение ряда специфических задач неукладывающееся в рамки обыкновенной алгебры.

Попытаемся вникнуть в суть необыкновенной алгебры на примере контактных схем электротехники.

1) Пусть к источнику тока подключена цепь, состоящая из лампочки и последовательно соединенных проводников, на которых контакты a и b размыкаются и замыкаются в различных вариантах (рис.1). Здесь символ 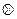означает, что лампочка горит, а О - лампочка не горит.

Обозначим цифрой 0-ноль, что контакт разомкнут, и тока нет, а цифрой 1- контакт замкнут. В итоге получим таблицу 1.

Очевидно, в этой таблице итог выражает действие умножения 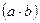в алгебре контактных схем. Ведь здесь, наприм.1, получается не как результат 1+1, а как 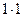=1. И далее: ,

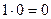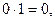
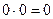-все это не противоречит здравому смыслу.

Другими словами, в алгебре контактных схем, действие умножения 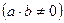состоит в том, что должны быть замкнуты одновременно оба контакта (и контакт и контакт b) последовательно соединенной цепи.

a b

a b

a b

a b

Рис.1

Таблица 1.

a	b	итог

2)Пусть к источнику тока подключена цепь, состоящая из лампочки и параллельно соединенных проводников, на которых контакты a и b замыкаются и размыкаются в различных вариантах (рис 2).В итоге получается таблица 2.

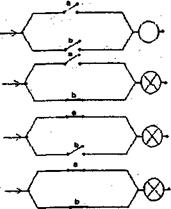
Рис.2

Таблица 2.

a	b	итог

Очевидно, теперь итог выражает действие сложения (a+b) в алгебре контактных схем. Ведь здесь, например 1, получается не как результат 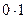, а как 0+1=1.И далее: 1+0=1, 0+0=0,

1+1=1- все это не противоречит здравому смыслу, если учесть что, 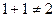так как и теперь через лампочку пройдет тот же ток что и ранее. Т.е. в алгебре контактных схем нет числа 2 вообще, а есть только числа 0 и 1.

Другими словами, в алгебре контактных схем, действие сложения 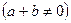состоит в том, что в цепи из параллельно соединенных проводников должен быть замкнут или только контакт b, или a и b вместе.

Таким образом, на примере контактных схем, мы ввели две основные операции (a*b и a+b) алгебры Буля: алгебры двух чисел («0» и «1»), или все равно алгебры двух высказываний («разомкнута» и «замкнута») или алгебра двух событий («невозможного» и «достоверного»). Мы займемся последним вариантом алгебры Буля и для начала сформулируем понятия основных операций алгебры событий.

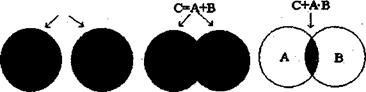
Определения: 1) Суммой двух несовместных событий A и B называется событие C=A+B состоящая в появлении только одного из этих событий, т.е. или только А, или только В (см. для наглядности контактные схемы рис.2. или круги Эйлера рис.3).

2) Суммой двух совместных событий А и В называется событие С=А+В состоящее в появлении хотя бы одного из этих событий (рис.2. или рис.4.)

3) Произведением двух событий А и В называется событие 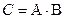состоящая в совместном появлении этих событий (т.е. и А и В) (рис.1. и рис.5).

С=А+В

Рис.3. рис.4. рис.5.

Аналогично определить сумму и произведение нескольких событий. Теперь перейдем к правилам вычисления вероятностей суммы и произведения двух событий.

1.Правило умножения.Вероятность произведения 2-х совместных зависимых событий равна произведению вероятности одного из этих событий на условную вероятность другого. Т.е.

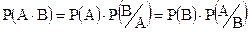
Доказательство. Рассмотрим следующую схему случаев:

1) Событие А наступило В нет - случаев

2) Событие В наступило А нет - случаев

Наступили события и А и В - 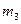случаев.

Здесь 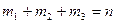- общее число случаев, т.е. полная система событий. Теперь по классической формуле будем иметь

;

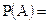
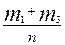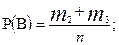
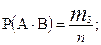
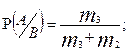
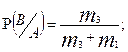
Искусственно преобразуем 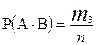, так

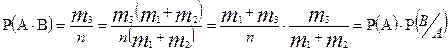
Аналогично можно доказать, что

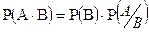
В частном случае, когда события независимые выше подчеркнутое
равенство принимает вид

,|

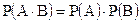а для несовместных событий будет

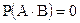
2. Правило сложения. Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без вероятности их произведения. Т.е.

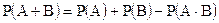
Доказательство. Используя выше приведенную схему случаев, будем иметь Р(А+В) = Р (или А или В или они вместе) =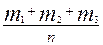

Запишем полученное равенство искусственно так

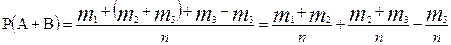
Отсюда следует искомое равенство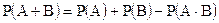

Эта формула, с помощью двух выше подчеркнутых равенств примет вид:

1) для несовместных событий

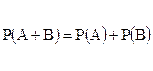
2) для совместных зависимых событий

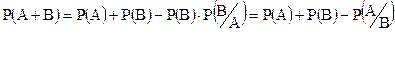
3)для совместных независимых событий

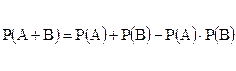
Можно убедиться в справедливости равенства

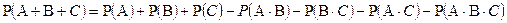
Следствие 1. Вероятность полной системы событий равна единице.

Доказательство.Пусть 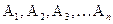-полная система событий. (Например, выпадение очков: 1, 2, 3, 4, 5,6 при подбрасывании игральной кости). Очевидно, будет ( 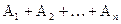)- достоверное событие (ведь обязательно выпадет или 1 очко, или 2 очка, или ..., или 6 очков).

Следовательно:

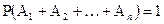
Здесь, по условию, событие 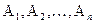образует полную систему, значит они единственно возможны и потому- несовместны.

Следствие 2.Вероятность события противоположного данному равна разности между 1 и вероятностью данного события.

Доказательство.Из последнего равенства следует, с учетом того, что А и несовместны:

Р(А + ) = 1 => Р(А) + Р( ) = 1

Теперь, из последнего равенства имеем

Р( ) = 1-Р(А) что и т.д.

Очевидно, справедливо и равенство Р(А) = 1-Р( ). Кстати, оба эти равенства удобны еще и тем, что их можно распространить на большое число совместных независимых событий.

Например, пусть: 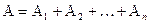означает, что хоть одно из произошло (где i =1,2,...n), тогда 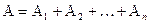означает, что не произошло ни одно из событий . Теперь равенство Р(А) = 1-Р(А) примет вид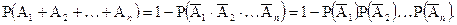

Следствие 3.Из последнего равенства следует, если

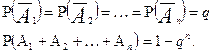
Для удобства решения задач объединим все выше выведенные формулы в следующую таблицу.

Таблица основных формул алгебры событий

несовместные 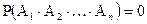(1)

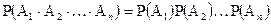↑ (2)

Случайные события

↓ независимые

совместные ↕

зависимые 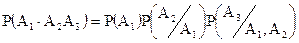(3)

несовместные 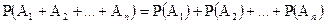(4)

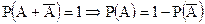↑ (5)

Случайные события

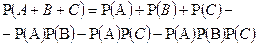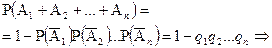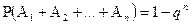(6) ↓ независимые (7) (8)

совместные ↕

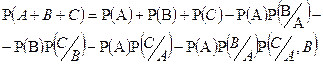зависимые (9