Учет взаимно индуктивных связей при решении задач анализа электрических цепей

Методические указания

При подготовке к занятию необходимо ознакомиться с соответствующими разделами теории по учебной литературе: [1, с.242–252]; [2, с.142–161]; [3, с.114–120].

Ответьте на вопросы:

1. Дайте толкование явлению взаимной индукции и для двух индуктивных катушек введите понятия собственных ( , ) и взаимной (М) индуктивностей. Определите коэффициент k магнитной связи двух катушек.

2. Как в схемах, в уравнениях цепи учитывается тот факт, что в зависимости от направления намотки витков катушек, а также в зависимости от направления токов магнитные потоки в каждой из катушек, собственные и взаимные, могут складываться, а могут вычитаться? Расскажите о маркировке катушек.

3. Запишите уравнения по второму закону Кирхгофа для последовательно соединенных индуктивно – связанных элементов при согласном и встречном включении в комплексной форме.

При решении задачи 8.3 следует учесть, что на рис.8.2, б представлен один из вариантов схемы Бушеро, служащей для получения тока в нагрузке, не зависящего от величины сопротивления нагрузки.

Рекомендуется не только получить численное значение тока , но и исследовать, от каких факторов зависит его величина. Целесообразно также сопоставить численные результаты всех решаемых в аудитории вариантов задачи 8.3.

З а д а ч а 8.1

Для схемы, изображенной на рис.8.1 и соответствующей заданному варианту, вычислите неизвестные величины (табл.8.1) и постройте векторную диаграмму токов и напряжений.

Рис.8.1

Таблица 8.1

Исходные данные к задаче 8.1

Вариант	Схема рис.8.1		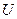				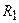		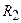	Определить
В	А	Ом	Ом	Ом	Ом	Ом	Ом
	в)		–
	а)	–							–
	г)	–
	б)		–					1,5	–
	в)		–
	г)								–
	а)	–							–

Окончание табл.8.1

Вариант	Схема рис.8.1		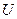				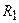		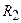	Определить
В	А	Ом	Ом	Ом	Ом	Ом	Ом
	в)	–
	б)	–						3,5	–
	в)								–
	г)		–
	а)		–						–
	в)	–
	б)		–						–
	г)		–
	б)	–							–
	в)	–
	а)		–					1,5	–
	г)								–
	в)		–
	в)	–							–
	б)	–							–
	г)		–
	а)	–							–
	в)								–
	г)								–
	б)		–						–
	в)								–
	г)		–
	в)		–

З а д а ч а 8.2

В цепи, представленной на рис.8.2,а, определите токи и напряжения между указанными точками при значениях параметров элементов, указанных в табл.8.2.

Рис.8.2

Таблица 8.2

Исходные данные к задаче 8.2

Вариант		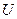		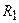		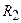			Способ включ.	Искомое напряж.
В	Ом	Ом	Ом	Ом	Ом	Ом	Ом
									встреч.
									согл.
									встреч.
									встреч.
									согл.
									согл.
									встреч.
									согл.
									встреч.
									согл.
									встреч.
									согл.
									встреч.
									согл.
									встреч.
									согл.
									встреч.
									согл.
									встреч.

Окончание табл.8.2

Вариант		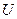		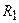		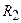			Способ включ.	Искомое напряж.
В	Ом	Ом	Ом	Ом	Ом	Ом	Ом
									согл.
									встреч.
									согл.
									встреч.
									согл.
									встреч.
									согл.
									встреч.
									согл.
									встреч.
									согл.

З а д а ч а 8.3

Для схемы (рис.8.2, б) определите токи , постройте векторную диаграмму токов и напряжений. В схеме (табл.8.3).

Таблица 8.3

Исходные данные к задаче 8.3

Вариант		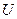			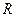Вариант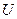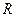
В	Ом	Ом	Ом	В	Ом	Ом	Ом
								7,5
								7,5

Окончание табл.8.3

Вариант		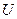			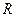Вариант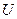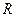
В	Ом	Ом	Ом	В	Ом	Ом	Ом
								7,5
								7,5
								7,5
								7,5
								7,5
								7,5
								7,5
								7,5

ЗАНЯТИЕ 9

РАСЧЕТ ТОКОВ И НАПРЯЖЕНИЙ В ЛИНЕЙНЫХ ЦЕПЯХ

С ПЕРИОДИЧЕСКИМИ НЕСИНУСОИДАЛЬНЫМИ ИСТОЧНИКАМИ

Методические указания

При подготовке к занятию необходимо ознакомиться с соответствующими разделами теории по учебной литературе: [1, c.299–309]; [3, с. 200–219].

Ответьте на вопросы:

1. Пусть несинусоидальный источник напряжения, действующий в цепи, описывается функцией времени u(t), период которой Т. В соответствии с теорией ряда Фурье этот источник может быть представлен бесконечной суммой:

.

Как называют , когда k >1? Как вычислить w? Во сколько раз частота k-й гармоники больше частоты основной гармоники?

2. Ряд Фурье, приведенный в п.1, можно представить в виде

.

Приведите формулы, связывающие и с . Покажите, как можно вычислить , если известны и .

3. Приведите все подобные выражения для случая периодического несинусоидального источника тока j(t).

4. Сообразуясь с определенной точностью расчета, можно представить периодический несинусоидальный источник в виде конечной суммы

.

Каким принципом, справедливым для линейных цепей, целесообразно воспользоваться, чтобы рассчитать токи в цепи от каждого из слагаемых приведенной суммы в отдельности?

Чему равно сопротивление индуктивного элемента для постоянной составляющей? Чему равно сопротивление емкостного элемента для постоянной составляющей?

Чему равно сопротивление индуктивного элемента для первой гармоники? Чему равно сопротивление емкостного элемента для первой гармоники?

То же – для k-й гармоники?

5. Применим ли при этих расчетах символический (комплексный) метод? На каких этапах?

6. Сформулируйте алгоритм анализа (порядок расчета токов, напряжений) линейных электрических цепей при несинусоидальных источниках.

7. Гармонический состав тока, напряжения известен. Как подсчитать его действующее значение?

8. Гармонические составы напряжения и тока на входе двухполюсника известны. Как вычислить активную мощность, коэффициент мощности?

9. Периодический сигнал может обладать некоторыми видами симметрии: а) симметрия относительно оси времени (оси абсцисс); б) симметрия относительно оси ординат; в) симметрия относительно начала координат.

Сформулируйте математические условия, отвечающие каждому из видов симметрии.

В каких случаях симметрии отсутствует постоянная составляющая? Четные гармоники? У всех гармоник начальная фаза равна нулю? У всех гармоник начальная фаза равна ±90⁰?

Какие виды симметрии зависят от выбора номера начала отсчета времени?

З а д а ч а 9.1

Выберите в соответствии с вариантом из табл.9.1, 9.2 общий вид разложения в ряд Фурье периодической несинусоидальной э.д.с. е(wt).

Рассчитайте постоянную составляющую, амплитудные значения и начальные фазы каждой гармонической составляющей заданного разложения и сформируйте выражение е(wt).

Таблица 9.1

Исходные данные к определению е(t)

Вариант

Рис. е(wt) из табл.9.2

Em, B

a

f, Гц

Вариант

Рис. е(wt) из табл.9.2

Em, B

a

f, Гц

Вариант

Рис. е(wt) из табл.9.2

Em, B

a

f, Гц

p/4

p/8

p/3

p/4

p/8

p/3

p/4

p/6

p/3

p/4

p/6

p/3

p/4

p/6

p/3

p/4

p/6

p/3

p/8

p/6

p/3

p/8

p/6

p/3

p/8

p/3

p/3

p/8

p/3

p/3

З а д а ч а 9.2

Определите мгновенное значение тока в цепи, представленной на схеме рис.9.1. На входе цепи действует источник э.д.с. е(wt), полученный в виде разложения в ряд Фурье в задаче 9.1 (табл.9.1, 9.2).

Рис.9.1. Схемы к задаче 9.2

Таблица 9.2

Описание функции к задаче 9.1

№ графика	График е(wt)	Разложение в ряд е(wt)
		е(wt)= +
		е(wt)=
		е(wt)=

Продолжение табл.9.2

№ графика	График е(wt)	Разложение в ряд е(wt)
		е(wt)=
		е(wt)=
		е(wt)=

Таблица 9.3

Исходные данные к задаче 9.2

Вариант	е(wt) из табл.9.1, 9.2	Схема	R, Ом	wL, Ом	, Ом	Вариант	е(wt) из табл.9.1, 9.2	Схема	R, Ом	wL, Ом	, Ом
		9.1,а			–			9.1,б		–
		9.1,б		–				9.1,а			–
		9.1,а			–			9.1,б		–
		9.1,б		–				9.1,а			–
		9.1,а			–			9.1,б		–
		9.1,б		–				9.1,а			–
		9.1,а			–			9.1,б		–
		9.1,б		–				9.1,а			–
		9.1,а			–			9.1,б		–
		9.1,б		–				9.1,а			–
		9.1,а			–			9.1,б		–
		9.1,б		–				9.1,а			–
		9.1,а			–			9.1,б		–
		9.1,б		–				9.1,а			–
		9.1,а			–			9.1,б		–

З а д а ч а 9.3

Для каждого из вариантов определите мгновенное значение тока i₁(t) в схеме табл.9.5, если мгновенное значение е(wt) определено данными табл.9.1, 9.2, а параметры заданы в табл.9.4.

Таблица 9.4

Исходные данные к задаче 9.3

Вариант	Схема из табл.9.5	R1, Ом	R3, Ом	wL1, Ом	wL2, Ом	wL3, Ом	, Ом	, Ом	, Ом
						–	–		–
				–		–	–		–
		–				–	–		–
				–		–			–
		–		–		–			–
			–				–		–
			–	–			–		–
		–	–				–		–
			–	–					–
		–	–	–					–
			–			–	–
			–	–		–	–
		–	–			–	–
			–	–		–
		–	–	–		–
						–	–		–
				–		–	–		–
		–				–	–		–
				–		–			–
		–		–		–			–
			–				–		–
			–	–			–		–
		–	–				–		–
			–	–					–
		–	–	–					–
			–			–	–
			–	–		–	–
		–	–			–	–
			–	–		–
		–	–	–		–

Таблица 9.5

Схемы к задаче 9.3

Вариант	Схема	Вариант	Схема	Вариант	Схема
1, 16		6, 21		11, 26
2, 17		7, 22		12, 27
3, 18		8, 23		13, 28
4, 19		9, 24		14, 29
5, 20		10, 25		15, 30

З а д а ч а 9.4

Для каждого из вариантов (табл.9.6) определите значение активной мощности, потребляемой двухполюсником, по заданным мгновенным значениям входного тока i и входного напряжения u. Определите действующие значения тока I и напряжения U.

Таблица 9.6

Исходные данные к задаче 9.4

Вариант	Мгновенное значение входного напряжения, В	Мгновенное значение входного тока, А
	u=100+70sinwt+50sin3wt	i=10+5sin(wt–300)–3sin(3wt–600)
	u=100+40sinwt+10sin5wt	i=10+2sin(3wt+100)–1sin(5wt–450)
	u=50+35sinwt+20sin2wt	i=2+1,5sin(wt–300)+0,5sin2wt
	u=25+15sin3wt+10sin(5wt+300)	i=5+3sin(3wt+450)+2sin5wt
	u=70+45sinwt+30sin3wt	i=7+5sin(wt–300)+6sin(3wt+300)
	u=100sinwt+30sin3wt+10sin5wt	i=10sin(wt+60)+3cos3wt+2cos5wt
	u=70+70sinwt+50sin3wt	i=10+5sin(3wt+600)+2sin5wt
	u=7sinwt+5sin(3wt+100)+2cos5wt	i=0,7sin(wt+450)+0,1sin5wt
	u=30+10sin(wt+300)+5cos2wt	i=3+3,7sinwt+1,4sin(2wt–100)
	u=10+70sin3wt+10cos5wt	i=5+3sin(wt+450)+2sin5wt
	u=100+70sinwt+50sin5wt	i=10+5sin(wt+450)+2sin(5wt+100)
	u=100sinwt+70sin5wt+10sin7wt	i=10sin(wt+450)+7sin(5wt+300)
	u=30+20sin3wt+5sin5wt	i=10+7sin(3wt–300)+2sin(5wt+100)
	u=9sinwt+4sin2wt+2sin5wt	i=4sin(wt+200)+2sin(2wt+600)
	u=20+10sin3wt+2sin(5wt+300)	i=2+0,1sin(3wt+600)+0,01sin5wt
	u=50+40sin3wt+20sin(5wt+100)	i=5+4sin(3wt–150)+2sin5wt
	u=70+60sin(3wt+100)+30sin5wt	i=3+6sinwt–5sin(5wt+600)
	u=9sinwt+8sin3wt+3sin5wt	i=9sin(wt+360)+0,8cos3wt
	u=9+10sin3wt+1,8sin5wt	i=5sin(3wt+300)+cos5wt
	u=12+11sin3wt+5sin5wt	i=3+2sin(3wt+500)+0,5cos5wt
	u=12sinwt+4cos5wt+2sin7wt	i=2sin(wt+500)+0,5sin(5wt+150)
	u=10sinwt+5sin3wt+2cos5wt	i=5sinwt+3cos(3wt+300)
	u=100+70sin(3wt+100)+50sin5wt	i=5+3cos3wt+2sin(5wt+450)
	u=10+30sinwt+2cos5wt	i=4+12sin(wt–150)+2sin5wt
	u=20sinwt+9sin2wt+7sin6wt	i=2sin(wt+100)+0,7sin(6wt–150)

Продолжение табл. 9.6

Вариант	Мгновенное значение входного напряжения, В	Мгновенное значение входного тока, А
	u=10+10cos2wt+7sin6wt	i=5sin(2wt+50)+2sin(6wt+100)
	u=50+40sin3wt+25cos5wt	i=5+4sin(3wt+150)+2sin5wt
	u=20+10sin2wt+5sin6wt	i=4+2sin(2wt+400)+cos6wt
	u=90+70sinwt+50sin3wt	i=9+7sin(wt+50)+5sin(3wt–150)
	u=100+80sin4wt+20sin6wt	i=5+2sin(4wt+300)+cos6wt

З а д а ч а 9.5

В цепи, схема которой показана на рис.9.2, определите неизвестные параметры. Исходные данные приведены в табл.9.7.

Рис.9.2. Схема к задаче 9.5 Рис.9.3. Схема к задаче 9.6

Таблица 9.7

Исходные данные к задаче 9.5

Вариант	u(t), В	w, с–1	Дополнительные исходные данные	Определить
	50sinwt+30sin3wt		, В R1=10 Ом, С=141 мкФ	L, R2
	41,54sinwt+40sin3wt		А R1=10 Ом, R2=10 Ом, L=31,9 мГн	С, y
	30,6sinwt+20sin5wt		, В R2=10 Ом, С=40,6 мкФ	L, R1

Продолжение табл.9.7

Вариант	u(t), В	w, с–1	Дополнительные исходные данные	Определить
	23,6sinwt+5sin5wt		, В R1=2 Ом, R2=3 Ом, L=4,77 мГн	С, y
	7,5sinwt+4sin3wt		А R1=1 Ом, С=88 мкФ	L, R2
	30,15sinwt+10sin3wt		, В R2=3 Ом, L=5 мГн	С, R1
	20,6sinwt+12sin3wt		А R1=R2=3 Ом, L=6 мГн	С, y
	30sinwt+10sin3wt		, В R1=2 Ом, С=55 мкФ	L, R2
	20,4sin3wt+7sin7wt		А R1=3 Ом, L=5 мГн	С, R2
	30,6sinwt+20sin5wt		, В R1=2 Ом, L=6 мГн	С, R2
	60sin3wt+15sin7wt		, В R2=4 Ом, С=25,5 мкФ	L, R1
	45sin3wt+28sin5wt		А R1=R2=5 Ом, С=63,4 мкФ	L, y
	15sinwt+6sin3wt		А R1=1 Ом, R2=2 Ом, L=3,18 мГн	С, y
	100sin3wt+56sin5wt		А, R1=5 Ом, L=7 мГн	С, R2
	30sinwt+5sin5wt		, В; R2=4 Ом, L=6 мГн	С, R1
	50sinwt+30sin3wt		А; R1=10 Ом, L=31,9 мГн	С, R1

Окончание табл.9.7

Вариант	u(t), В	w, с–1	Дополнительные исходные данные	Определить
	30,6sinwt+20sin5wt		, В R1=5 Ом, R2=10 Ом, С=40,6 мкФ	L, y
	41,54sinwt+40sin3wt		,В, R2=10 Ом, С=141 мкФ	L, R1
	23,6sinwt+5sin5wt		А R1=2 Ом, С=21,2 мкФ	L, R2
	7,5sinwt+4sin3wt		, В R1=1 Ом, R2=3 Ом, L=3,18 мГн	С, y
	30,15sinwt+20sin3wt		А R1=2 Ом, R2=3 Ом, С=185 мкФ	L, y
	20,64sinwt+12sin3wt		, В, R2=3 Ом, С=74 мкФ	L, R1
	30sinwt+10sin3wt		А R2=4 Ом, L=8 мГн	С, R1
	20,4sin3wt+7sin7wt		, В R2=4 Ом, С=25,5 мкФ	L, R1
	30sinwt+5sin5wt		А R1=2 Ом, R2=4 Ом, С=30,1 мкФ	L, y
	45sin3wt+28sin5wt		, В R2=5 Ом, L=7 мГн	С, R1
	60sin3wt+15sin7wt		А R1=3 Ом, R2=4 Ом, L=5 мГн	С, y
	20sinwt+8sin5wt		А R2=4 Ом, С=30,1 мкФ	L, R1
	85sinwt+56sin3wt		, В R1=5 Ом, C=63,4 мкФ	L, R2
	60sinwt+50sin3wt		, В R2=3 Ом, L=15 мГн	С, R1

З а д а ч а 9.6

Определите неизвестные параметры цепи (рис.9.3). Исходные данные приведены в табл.9.8.

Таблица 9.8

Исходные данные к задачам 9.6, 9.7