Определение несобственного интеграла от неограниченной функции на ограниченном промежутке

Пусть функция y = f (x) не ограничена на отрезке [a;b], однако интегрируема на любом меньшем отрезке [a;b-эпсил], где эпсил>0. Тогда если существует предел 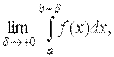,его принимают за несобственный интеграл от неограниченной функцииf (x):

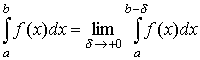Если предел существует несобственный интеграл называется сходящимся, в противном случае — расходящимся.

50.Расстояние в Rⁿ. Свойства расстояния.

Окрестность точки в Rn . Внутренние и граничные точки множества.

Пусть pₒ- точка в Rⁿ и ε – положительное число. Открытым шаром, или просто шаром радиуса ε с центром в pₒ называется множество всех точек, расстояние которых от pₒ меньше ε:

{p € Rⁿ │ ρ (pₒ,p)< ε}.

Шар радиуса ε с центром pₒ обозначается B(pₒ, ε) или U3(pₒ). Множество U3(pₒ) называют

ε–окрестностью точки pₒ.

Внутренние и граничные точки множества:

Пусть Х – множество в пространстве Rⁿ. Точка р называется:

-Внутренней точкой множества Х, если она содержится вместе с некоторой своей

ε–окрестностью;

-Внешней точкой по отношению к Х, если она является внутренней для дополнения Х в Rⁿ;

-Граничной точкой для Х, если она не является ни внутренней ни внешней точкой для Х, иначе говоря, если любая ее окрестность содержит как точки, принадлежащие Х, так и точки, не принадлежащие Х.

Открытые и замкнутые множества.

Множество X называется открытым, если все его точки внутренние.

Множество X называется замкнутым, если оно содержит все свои граничные точки.

Изолированные и предельные точки множества.

Пусть X - множество в Rn. Точка p0 называется предельной для X, если в любой

ε-окрестности точки p0 имеются точки множества X, отличные от p0.

При этом сама точка p0 может как принадлежать, так и не принадлежать множеству X.

Точка p0принадлежащая X называется изолированной точкой множества X, если у нее существует ε-окрестность, в которой никаких других точек из X, кроме p0, нет.

Ясно, что любая точка множества Х является либо изолированной, либо предельной

для Х.

Ограниченные множества.

Множество Х принадлежащRⁿназывается ограниченным, если оно целиком содержится в некотором шаре. Пустьр₀ – точка в Rⁿ , а эпсилон – положительное число, тогда Шаром радиуса эпсилон с центром р₀ называется множество всех точек, расстояние которых от р₀ меньше эпсилон.

55.Сходимость последовательности точек в Rn , ее эквивалентность покоординатной сходимости.

56.Функция нескольких переменных.

Способ, который каждой точке х Rⁿ ставит в соответствие единственную точку у R^m, называется функцией многих переменных.