Обоснование степенного метода

Лекция 11

Степенной метод и метод Якоби

Степенной метод

Обоснование степенного метода

В случае симметричной матрицы 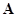все ее собственные значения вещественны, и этим собственным значениям соответствуют 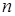линейно независимых собственных векторов . Система векторов образует базис в пространстве размерности 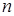, иными словами, любой вектор размерности 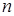можно представить в виде разложения по . Недоверчивые могут найти доказательство этих утверждений в книге [11.1].

Здесь и в дальнейшем будем нумеровать собственные значения в порядке возрастания

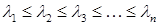. (11.1)

Возьмем произвольный вектор 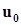размерности 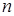. Хотя собственные вектора матрицы 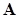нам еще не известны, мы знаем, что 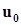можно представить в виде линейной комбинации собственных векторов:

. (11.2)

Вычислим вектор :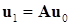

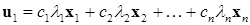. (11.3)

Здесь было использовано определение собственного вектора: .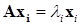

Повторяя эту операцию 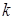раз, получаем

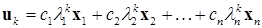. (11.4)

Согласно принятой нумерации (11.1), максимальным из собственных значений будет 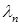. Поэтому в конце концов последнее слагаемое (11.4) должно намного превзойти все остальные, и 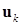в пределе должно совпасть по направлению с 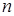-м собственным вектором, а отношение длин векторов 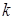-го и 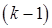-го приближений стремится к наибольшему собственному значению:

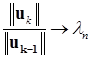. (11.5)

Единственное замечание, которое осталось сделать перед тем, как перейти к практическому применению степенного метода: вектор 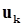следует каким-либо образом нормировать после каждого шага. Иначе этот вектор очень быстро вырастет до совершенно неприличных размеров. Например, можно очередное приближение вычислять следующим образом:

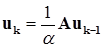, (11.6)

где 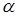– значение первой компоненты произведения 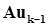. Кстати, в этом случае последовательность значений 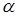должна сходиться к .

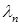Пример. Найдем степенным методом максимальное собственное значение и соответствующий собственный вектор матрицы:

.

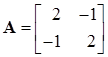Примем в качестве начального вектора и выполним несколько приближений:

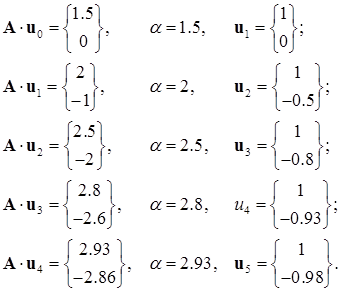
Как видим, результаты неуклонно приближаются к точному решению:

.

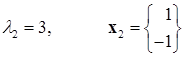Точное решение этого примера получено на предыдущей лекции.

Замечание.Сходимость степенного метода может быть медленной, когда 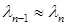, или даже вообще отсутствовать (так как возможно 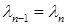). Поэтому на практике степенной метод обычно применяют, используя для итераций не один, а несколько ортогональных векторов:

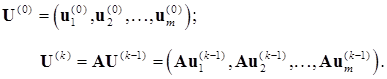(11.7)

После каждой итерации ортогональность векторов, естественно, нарушается. Поэтому перед очередным приближением полученные вектора ортогонализируют по методу Грама ‑ Шмидта. Помимо улучшения сходимости такой подход позволяет вычислить не одно, а несколько пар собственных значений и собственных векторов.

Обратный степенной метод

Применяя степенной метод, мы получаем наибольшее собственное значение 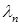и соответствующий собственный вектор 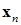. В задачах механики, как правило, наиболее интересны минимальные собственные значения 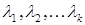. Так, в задачах о собственных колебаниях конструкции обычно практический интерес представляют несколько низших частот собственных колебаний.

В таких случаях удобнее использовать обратный степенной метод. Метод называется так потому, что итерации, аналогичные (11.6), выполняются не с самой исследуемой матрицей 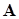, а с обратной к ней матрицей :

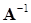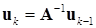. (11.8)

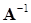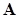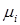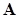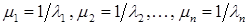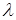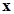Здесь используется тот факт, что матрица имеет те же самые собственные вектора, что и матрица , а соответствующие собственные значения являются величинами, обратными собственным значениям : . В самом деле, пусть и – собственная пара матрицы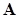

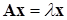. (11.9)

Тогда, умножая (11.9) слева на 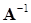, получаем

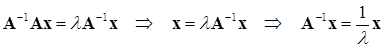. (11.10)

Таким образом, в результате использования итераций (11.8), мы должны получить максимальное собственное значение 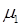матрицы 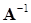и соответствующий собственный вектор , а, значит, и минимальное собственное значение 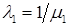матрицы 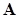с тем же собственным вектором .

Следует заметить, что обратный степенной метод вовсе не требует, как может показаться на первый взгляд, трудоемкого обращения матрицы. Выражение (11.8) можно переписать таким образом:

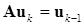(11.11)

Следовательно, для получения очередного приближения 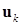надо только решить систему линейных уравнений (11.11) одним из методов, рассмотренных в первой части. Если, например, используется метод Холецкого:

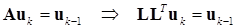, (11.12)

треугольное разложение матрицы достаточно выполнить только один раз. Тогда на каждой очередной итерации требуется только решить две треугольные системы.

Пример. Попробуем применить обратный степенной метод крассмотренной в разд. 6.1 матрице

.

Напомним, что в предыдущей лекции было получено точное решение:

; .

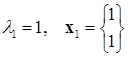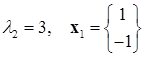Нетрудно убедиться, что

,

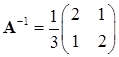тогда, приняв в качестве начального приближения

,

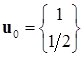получим

;

;

.
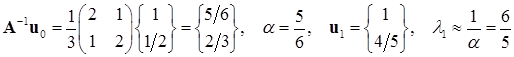
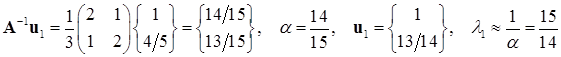
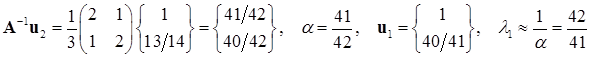