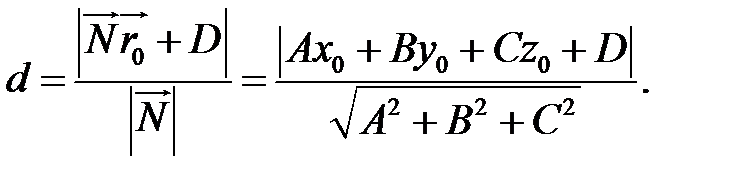Рівняння площини у відрізках на координатних осях. Рівняння площини, що проходить через три задані точки. Обчислення відстані від точки до площини

Розглянемо площину, яка у системі координат 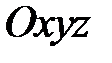задана загальним рівнянням , у якому 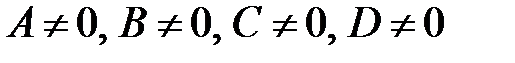. Тоді в результаті ділення обох частин на коефіцієнт 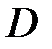це рівняння можна переписати у вигляді

,

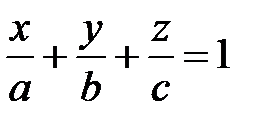де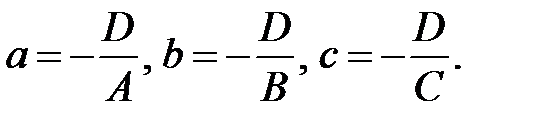

Можна бачити, що точки 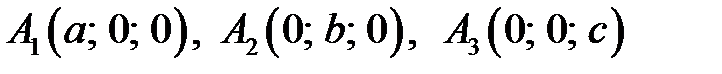задовольняють рівняння , тобто належать площині і є точками перетину цієї площини з осями координат (Рис.28.1).

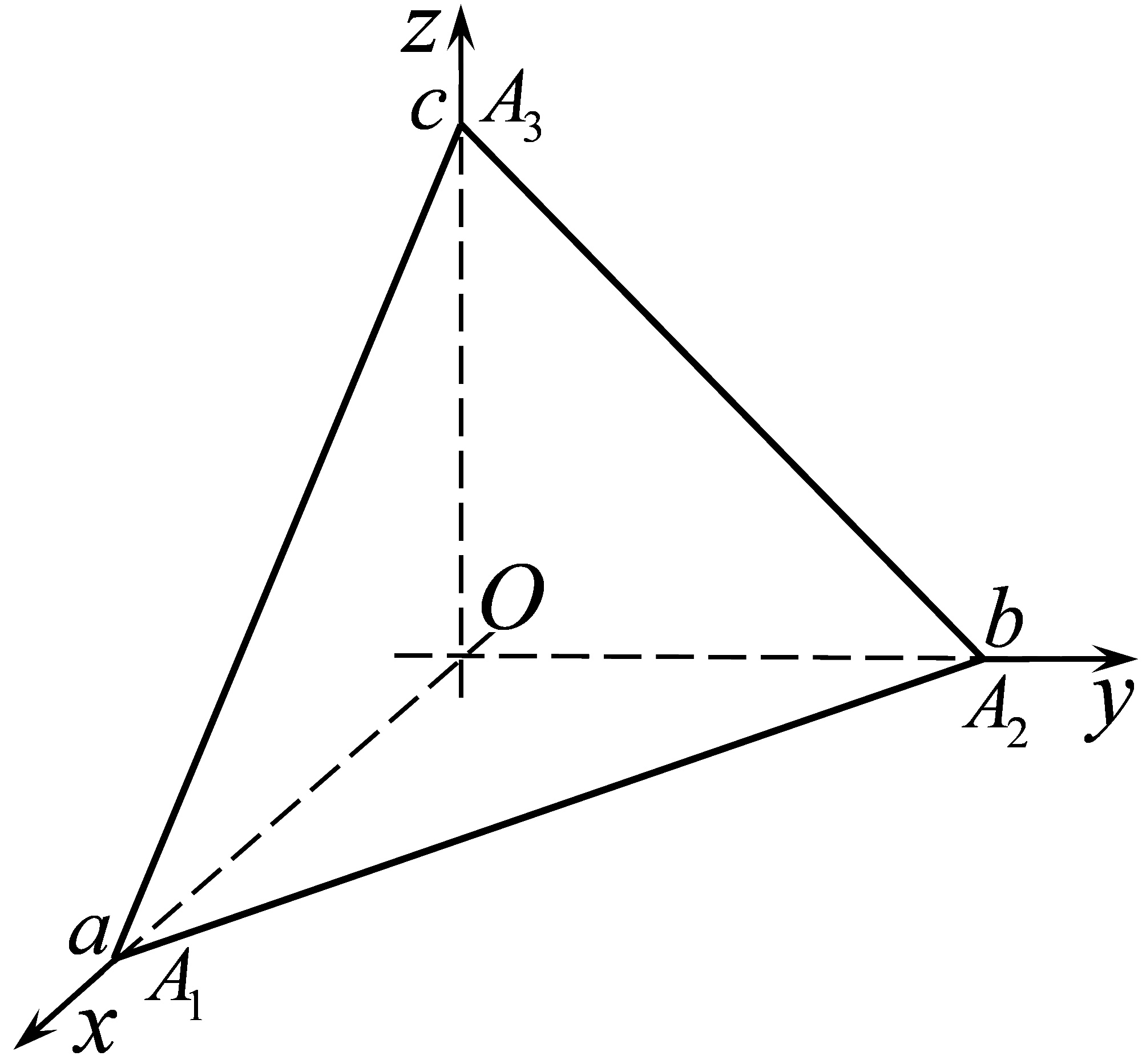
Рис. 28.1

Таким чином, якщо відомі точки перетину площини з осями координат, то її рівняння може бути записаним у вигляді . Оскільки числа 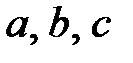з точністю до знаку співпадають з довжинами відрізків, які площини відтинає на координатних осях: 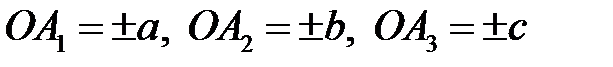, то рівняння ще називаються рівнянням площини у відрізкахна координатних осях.

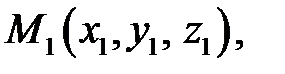
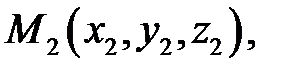
Розглянемо тепер три довільні точки 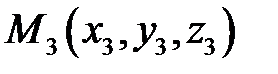, які не знаходяться на одній прямій. Як відомо, тоді існує єдина площина, що проходить через ці точки. Знайдемо її рівняння.

Для цього візьмемо на площині довільну точку 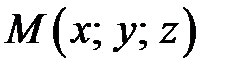і розглянемо вектори 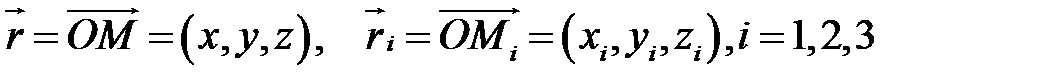(Рис.28.2):

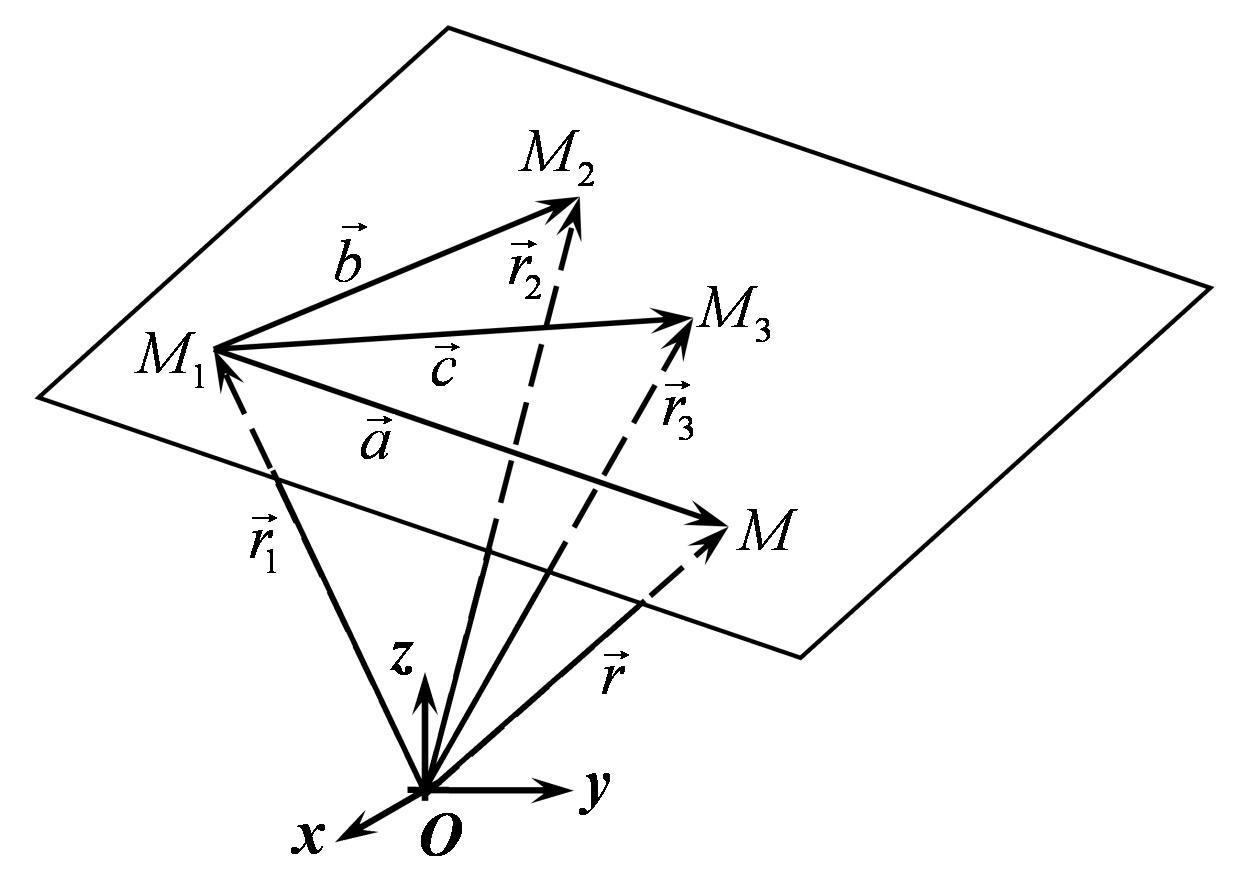
Рис. 28.2

Тепер, якщо взяти вектори 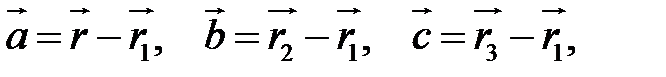то вони знаходяться у одній площині і є компланарними. Тоді їх мішаний добуток має дорівнювати нулю:

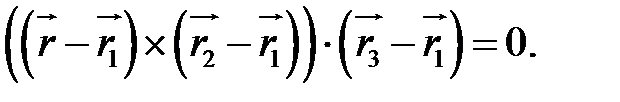
Рівняння містить 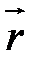- радіус-вектор довільної площини і є векторною формою рівняння площини, що проходить через три задані точки. Координатну форму рівняння отримаємо, коли скористаємося формулою для мішаного добутку:

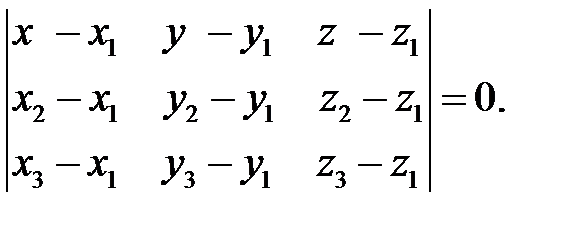
Після обчислення визначника перетвориться у лінійне рівняння відносно 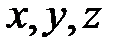, яке і є загальним рівнянням площини, що проходить через три задані точки.

Розв'яжемо методами аналітичної геометрії задачу, яка має важливе значення для теорії навігації і картографії. А саме, визначення відстані від заданої точки до заданої площини. Нехай у системі координат 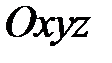задано точку 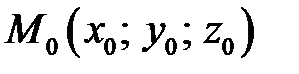і площину, яка визначається рівнянням . Проведемо з точки 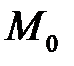на площину перпендикуляр, який перетне її у точці 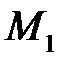(Рис.28.3). Тоді довжина цього перпендикуляра 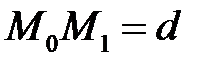і є відстань від точки до площини. 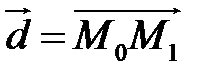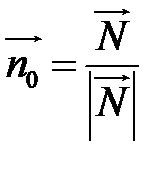Розглянемо вектори і - одиничний вектор, нормальний до площини.

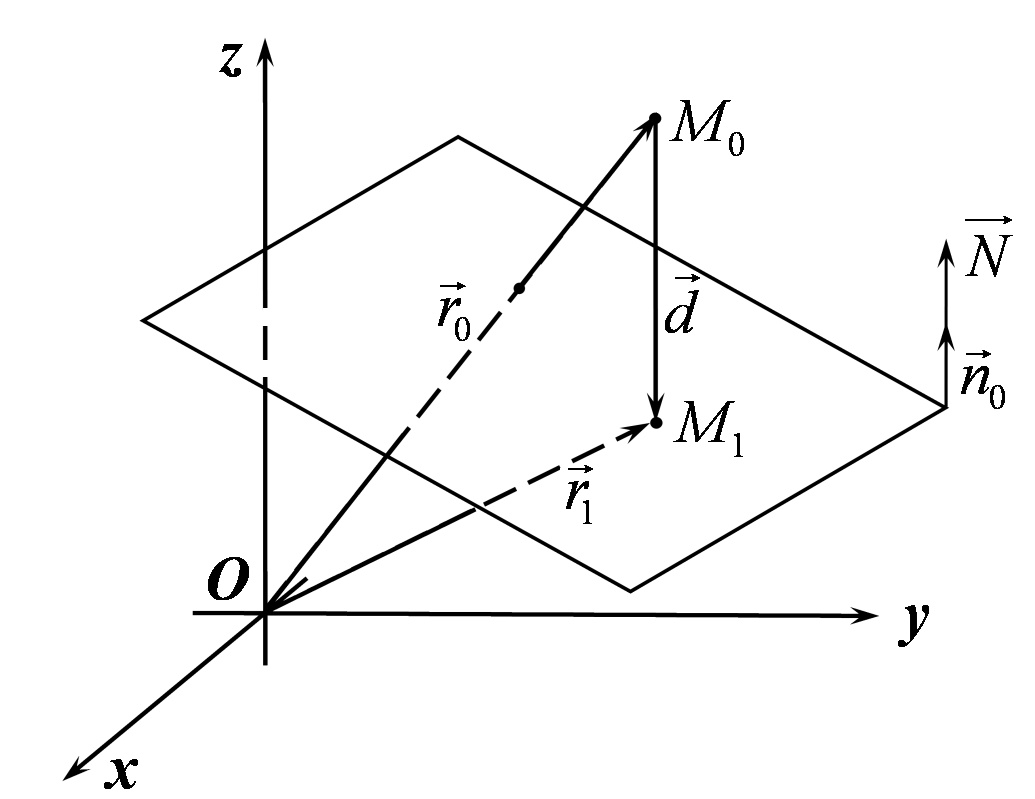
Рис. 28.3

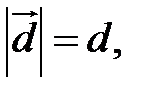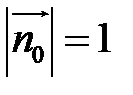Оскільки ці вектори колінеарні і а , то 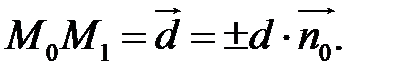Знак залежить від розміщення точки 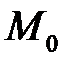відносно площини. Позначимо 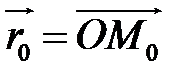, 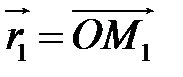. Тоді з векторного трикутника 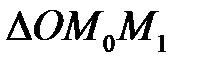(Рис.28.3) маємо:

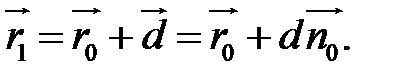
Але точка 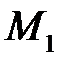належить площині і її радіус-вектор 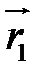має задовольняти векторне рівняння . В результаті підстановки у знаходимо

.

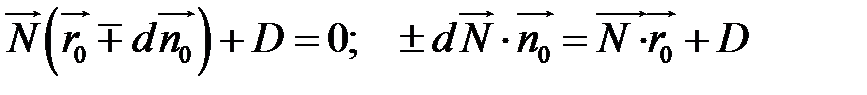Оскільки 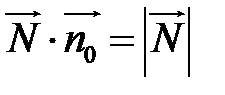, то .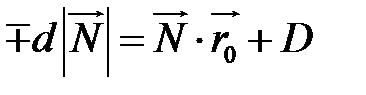

Абсолютні величини лівої та правої частин останньої рівності мають співпадати.

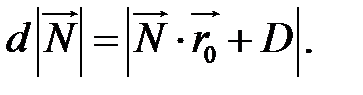
Остаточно знаходимо формулу для відстані: