Условия совместности деформаций

Прикладная теория упругости.

Теория упругости занимается изучением процесса деформирования упругих тел. Основная задача теории упругости — определение напряженно-деформированного состояния (НДС) нагруженного или нагретого тела.

Всюду в этом курсе будем изучать статический процесс деформирования, то есть будем считать, что отсутствует временной фактор.

Основные гипотезы теории упругости.

1. Гипотеза сплошности (континуума).

До деформации и после нее геометрический объем тела совпадает с материальным. Эта гипотеза позволяет широко использовать математический аппарат дифференциального и интегрального исчисления.

2. Гипотеза о малости перемещений и их градиентов.

Перемещения малы по сравнению с размерами тела, а градиенты (они безразмерные) намного меньше единицы. Мы ограничимся изучением геометрически линейных теорий, при описании которых перемещения и градиенты будут входить геометрически линейным образом. Все эти линейные зависимости пренебрегают градиентами по сравнению с единицей.

3. Физическая гипотеза (обобщенный закон Гука).

Меры внутренних сил (напряжений) связаны с мерами деформирования (деформациями) линейными зависимостями. Все теории, основанные на этой зависимости называются линейно-фиизическими.

4. Гипотеза о естественном состоянии тела.

В ненагруженном состоянии в телах отсутствуют напряжения и деформации.

Во всяком процессе деформирования можно выделить:

Геометрическую сторону. Она связана с изучением взаимного расположения точек тела при деформировании а также с изменением взаимного расположения точек. В дальнейшем увидим, что эти изменения могут быть полностью описаны деформациями.

Статическую сторону. Основными изучаемыми величинами являются внутренние силы, за которые мы будем принимать напряжения.

Физическую сторону. Здесь постулируется связь между напряжениями и деформациями.

Основная задача геометрической стороны процесса деформирования: введение понятия напряжений и деформаций как мер изменения взаимного расположения точек тела, а также в установлении взаимосвязи между деформациями и напряжениями.

Основная задача статической стороны: введение понятия мер внутренних напряжений и установлении их связей с заданными внешними силами.

Теория деформаций

Здесь изучается геометрическая сторона процесса деформирования.

Предположим, что известна система координат. Опишем положение тела до начала процесса деформирования. Будем характеризовать все точки вектором r

r =xi +у j +z k.

Предположим, что в процессе деформирования точка заняла другое положение, совершив перемещение

u (x, y, z) = u(r) = u i + v j + w k.

Будем считать, что uизвестно. То есть известны его компоненты u, v, w.

Берем точку А и произвольное направление t. Тогда

AB =dr, t =l i+ m j+ n k, |AB| =ds

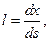
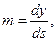
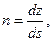
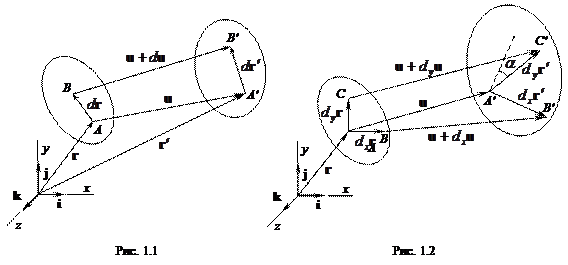dr = t /ds, |ds'| = |dr'| = |A' B'|

Определим деформацию удлинения в точке тела по некоторому фиксированному направлению tвыражением

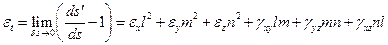
В результате преобразований получим

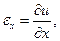
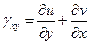
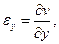
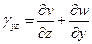(1.1)

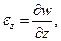
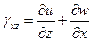
Примечание. Все формулы, выделенные красным цветом, рекомендуем знать или

понимать, как они получаются)

Предположим, что t || i. Тогда l =1, m=n=0, и 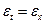— деформация удлинения вдоль оси 0x. Аналогично вдоль 0у и 0z. Они положительны, если волокна удлиняются.

Деформации 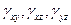описывают изменение прямого угла между соответствующими направлениям 0x, 0y, а также 0x, 0z и 0y, 0z в одной точке. Они положительны, если прямой угол уменьшается.

Величины 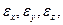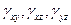называются декартовыми компонентами деформации. Их еще называют соотношениями Коши.

Матрица, составленная из этих компонент

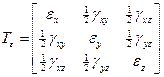
называется тензоромдеформаций. То есть этими выражениями определяются все декартовы линейные деформации в точке (удлинения и сдвиги).

По известным перемещениям всегда однозначно могут быть найдены деформации.

Условия совместности деформаций.

Посмотрим, как определяются перемещения при известных деформациях.

Если деформации заданы произвольно, то гипотеза сплошности может быть нарушена, и следовтельно, перемещения определяются неоднозначно. Деформаций шесть, а перемещений только три. Деформации поэтому нельзя задавать произвольно. Должны быть выполнены шесть условий их совместности, то есть условий их интегрируемости Их еще называют условиями "сплошности" перемещений.

Эти условия или уравнения определяются конструкцией выражений Коши для деформаций (1.1), вытекают из них и нося имя Сен-Венана.

……………………..

……………………..

……………………..

……………………..

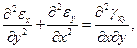
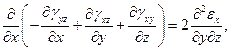
Если ход решения задачи организован так, что находятся перемещения, а потом - деформации, то соотношения их совместности не нужны,

В противном случае, то есть когда сначала ищутся деформации, а потом перемещения, все - иначе. Условия сплошности необходимы. Иначе взаимные противоречия в соотношениях Коши не позволят найти перемещения.

Итак, условия совместности = условия сплошности = соотношения Сен-Венана.

Теория напряжений

В процессе деформирования твердого тела участвуют два вида сил: внешние и внутренние. Внешние силы обычно считаются заданными, а внутренние — искомыми, определяемыми в ходе решения конкретной задачи.

Настоящий раздел целиком посвящен статической стороне процесса деформирования тела. Сущность раздела составляет связь между внешними и внутренними силами.

Внешние силы. Действующие на тело внешние силы можно разделить на поверхностные и объемные.

Поверхностные силы прикладываются к границе (поверхности) телa и возникают при контактном взаимодействии с другими телами или средами. Примером таких воздействий могут служить давление жидкости или газа (ветер), реактивные силы со стороны опор или других твердых тел и т.п.

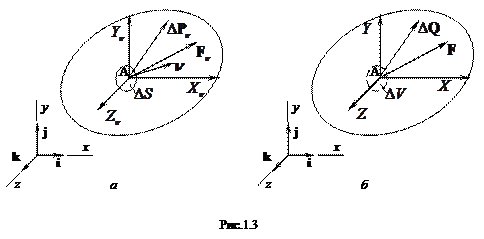Пусть тело в деформированном состоянии отнесено к прямоугольной декартовой системе координат Oхyz, единичные орты которой обозначим через 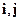и 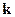, и пусть 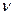— вектор единичной внешней нормали к поверхности тела в точке А (см. рис. 1.3 a). Предположим, что на элемент 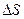поверхности, содержащей точку А, действует сила 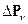. Тогда за меру поверхностных сил в точке А можнo принять векторную величину, определяемую соотношением

,

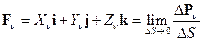(1.2)

где предельный переход осуществляется при стягивании элемента 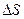поверхности в точку А. Вектор 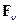имеет размерность [сила/длина² ] и именуется в литературе удельной поверхностной силой, интенсивностью или плотностью поверхностных сил. Его компоненты 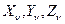считаются положительными, если направления векторов 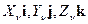совпадают с положительными направлениями соответствующих осей координат (независимо от направления внешней нормали к поверхности в рассматриваемой точке).

Объемные силы действуют в каждой точке тела и порождаются силовыми полями (гравитационными, электромагнитными и другими).

Примерами объемных сил могут служить силы веса, инерционные и другие силы. Мера объемных сил вводится по аналогии с поверхностными силами при помощи соотношения (см. рис.1.3 6)

,

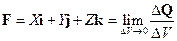(1.3)

где 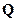— сила, действующая на элемент 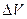объема тела в окрестности некоторой точки А внутри тела, а предельный переход осуществляется при стягивании элемента 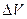объема в точку А. Вектор 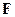называется удельной объемной силой (интенсивностью или плотностью объемных сил) и имеет размерность сила/длина. Компоненты 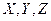считаются положительными, если направления векторов 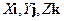совпадают с положительными направлениями соответствующих осей координат.

В дальнейшем, говоря о внешних силах, мы будем иметь в виду удельные внешние силы.

1.4.1. Напряжения. Под внутренними силами понимаются силы взаимодействия частей тела в процессе его деформирования. Для обнаружения их применим так называемый метод сечений, сущность которого заключается в следующем.

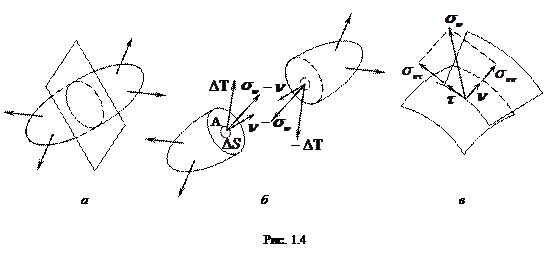Пусть деформируемое тело под действием внешних сил находится в состоянии равновесия (см. рис.1.4а). Рассечем его мысленно некоторой гладкой поверхностью на две части и отделим их друг от друга (см. рис.1.46). К поверхностям сечения обоих частей приложим силы, с которыми одна часть действует на другую. Для целого тела эти силы являются внутренними силами взаимодействия частиц, расположенных по обе стороны поверхности разреза, и по третьему закону Ньютона ониравны по величине и противоположны по направлению. В результате такого построения каждая из частей тела должна находится в равновесии (в противном случае из этих частей не удастся составить исходное, находящееся в состоянии равновесия тело). Рассмотрим, например, левую часть. По отношению к ней внутренние для всего тела силы взаимодействия являются поверхностными и согласно предыдущему пункту в некоторой точке А поверхности сечения их можно измерять вектором (см. рис. 1.4 6)

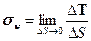
называемым вектором напряжений. Как видно он зависит от положения точки его приложения и направления нормали к поверхности его действия и имеет размерность сила/длина² .

Пусть С — линия пересечения поверхности сечения с плоскостью, содержащей

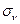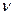векторы и , а 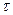— единичный вектор, касающийся этой кривой в точке А (см. рис. 1.4 в). Проекцию 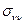( 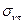) вектора напряжений 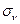на направление 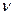( 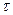) называют нормальным (касательным) напряжением.

Так как внутренние силы взаимодействия частей тела подчиняются третьему закону Ньютона, то (см.рис.1.4 6)

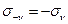(1.4)

Чаще всего нам придется рассматривать площадки, нормаль к которым параллельна одной из координатных осей. Пусть, например, 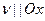. Тогда для вектора 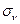можно использовать обозначение 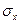, а для его проекций на оси координат — 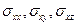(см. рис.1.5а), где первый индекс указывает направление нормали к площадке ( 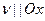), а второй — ось, на которую спроектирован вектор 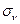. Аналогично рассматриваются и площадки, нормали к которым параллельны другим осям (см. рис.1.4 в). Девять составляющих

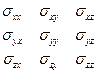
векторов 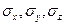на оси координат образуют так называемый тензор напряжений и называются компонентами тензора напряжений или просто напряжениями.

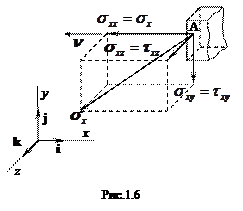
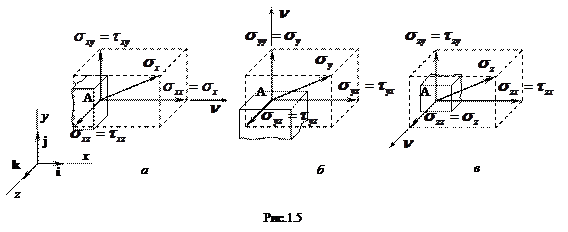Напряжения с одноименными индексами называются нормальными, а с разноименными — касательными. Правило знаков для них вытекает из рис. 1.5. Так, например, в случае, показанном на рис. 1.З а, нормаль к площадке направлена вдоль положительной оси 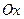и соответствующие напряжения считаются положительными, если их направления совпадают с положительными направлениями координатных осей. Если же нормаль 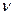к рассматриваемой площадке будет противоположна положительному направлению оси 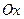, то согласно (1.4) положительные напряжения на этой площадке будут против положительных направлений осей координат (см. рис. 1.6).

1.4.2. Условия на поверхности. Уравнения равновесия. Пусть деформируемое тело находится в равновесии. Это означает, что главный вектор и главный момент действующих на него (как на абсолютно твердое тело) внешних сил должны равняться нулю, то есть

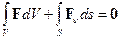	(1.5)
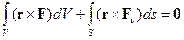	(1.6)

Здесь 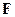, 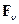— векторы интенсивностей объемных и поверхностных сил соответственно;

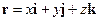(1.7)

— радиус-вектор рассматриваемой точки; 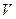, 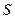— соответственно объем и площадь поверхности тела, a 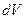и 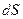— их бесконечно малые элементы.

Уравнения (1.5), (1.6) выражают необходимые и достаточные условия равновесия тела в целом и выполняются независимо от значений внутренних сил (напряжений). Вообще говоря, они имеют место в деформированном состоянии тела. Однако можно показать, что в рамках линейной теории и гипотезы о малости перемещений и деформаций уравнения равновесия, как и понятия о мерах внешних и внутренних сил, в деформированном и недеформированном состояниях совпадают. Поэтому исследование статической стороны процесса деформирования можно проводить в исходной геометрии тела.

Если тело находится в состоянии равновесия в целом, то, очевидно, и любая мысленно выделенная из него часть под действием приложенных к ней сил (включая напряжения) также будет находиться в состоянии равновесия. Этот факт позволяет установить связь напряжений с порождающими их внешними силами.

Связь напряжений с поверхностными силами можно найти из рассмотрения равновесия бесконечно малого объема, выделенного из тела в окрестности его границы, и последующего предельного перехода, когда этот элемент объема подобным образом стягивается в рассматриваемую граничную точку.

Пусть 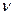— единичная внешняя нормаль к поверхности деформированного тела в некоторой ее точке А с координатами 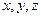. Возьмем в малой ее окрестности внутри тела на продолжении нормали 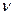другую точку 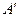с координатами 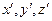(см. рис.1.7). Проведем через точку 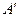три плоскости, параллельные координатным плоскостям, а через точку А — плоскость, касающуюся поверхности тела. В результате получим элемент объема тела в форме тетраэдра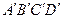

Уравнение равновесия действующих на тетраэдр сил имеет вид

,

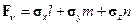(1.8)

Здесь

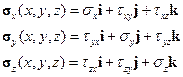
или в координатной форме

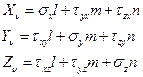(1.9)

Уравнения (1.9) устанавливают искомую связь между напряжениями и поверхностными силами. По своему физическому смыслу они отражают условия локального равновесия на границе тела и называются условиями на поверхности или статическими граничными условиями. Заметим, что они верны лишь на границе тела.

Связь напряжений с объемными силами можно вывести из рассмотрения равновесия элемента объема, выделенного в окрестности внутренней точки тела. Однако в этом нет необходимости, так как искомые соотношения являются следствием глобального равновесия тела (см. (1.5), (1.6)) и локального равновесия на границе (см.(1.8)).

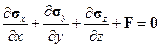(1.10)

или в координатной форме

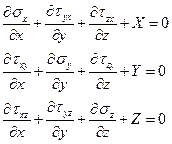(1.11)

Аналогичным образом преобразуется и уравнение (1.6) к виду

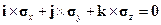
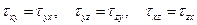(1.12)

Соотношения (1.12) принято называть законом парности касательных напряжений. Он показывает, что порядок следования индексов в обозначениях касательных напряжений несущественен, и служит доказательством симметричности тензора напряжений.

Если процесс деформирования носит временной характер, то в состав объемных сил следует включить силы инерции. Пусть 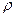— массовая плотность материала, из которого изготовлено тело. Тогда вектор плотности инерционных сил равен 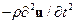, где через 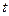обозначено время. Вводя в уравнение (1.10) вместо вектора объемной силы 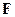вектор 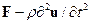, получим динамические уравнения равновесия в векторной форме:

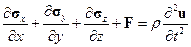(1.13)

Вид их в координатной форме очевиден.

1.4.3. Напряженное состояние в точке. Из предыдущих рассуждений следует, что значения напряжений зависят от положения точки и ориентации площадки, на которую они действуют.

Предположим, что в некоторой точке 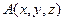внутри тела известны компоненты тензора напряжений, то есть, заданы вектора

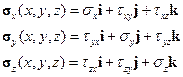(1.14)

действующие на площадки, перпендикулярные осям 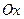, , 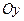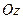соответственно. Покажем, что через эти величины выражаются, и притом единственным образом, напряжения на любой другой площадке, проходящей через эту же точку А.

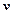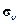Пусть ориентация площадки определена единичным вектором ее нормали , а — действующий на нее искомый вектор напряжений. Выделим мысленно в окрестности точки 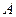бесконечно малый тетраэдр, три грани которого параллельны координатным плоскостям, а четвертая совпадает с рассматриваемой площадкой (см. рис.1.7). Исследуя равновесие этого тетраэдра по аналогии с предыдущим пунктом, найдём

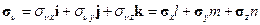(1.15)

или в координатной форме

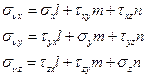(1.16)

Эти соотношения доказывают сделанное утверждение и позволяют полностью описать напряженное состояние в точке деформированного тела.

Остановимся на одном частном вопросе, обязанном с понятием главных напряжений и главных площадок. Главной называют площадку, на которую действует вектор напряжений, параллельный ее нормали. Численное значение 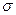длины этого вектора называется главным напряжением. Покажем, как с помощью формул (1.16) можно найти главные напряжения и положения главных площадок.

Из определения главного напряжения следует

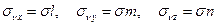(1.17)

Подставляя эти выражения в уравнения (1.16), получим

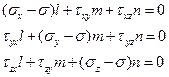(1.18)

К этой однородной системе линейных алгебраических уравнений относительно направляющих косинусов 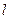, , 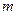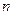нормали 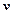следует добавить очевидное соотношение

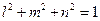(1.19)

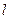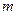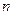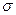Уравнений (1.18) ,(1.19) достаточно для нахождения четырех величин , , и . Действительно, нетривиальное (отличное от нуля) решение системы (1.18) существует, если

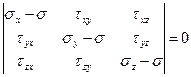
Раскрывая определитель, получим кубическое уравнение

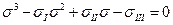(1.20)

коэффициенты которого имеют вид

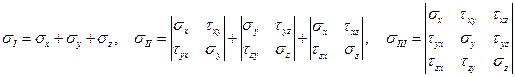(1.21)

С помощью закона парности касательных напряжений можно показать, что уравнение (1.20) имеет три действительных корня 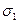, , 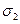, дающие значения главных напряжений. Для каждого из них можно найти решение системы (1.18), (1.19). Таким образом, в каждой точке тела существует три главные площадки. С помощью закона парности касательных напряжений можно показать, что главные площадки ортогональны друг другу.

Обобщенный закон Гука

Рассмотренные в двух предыдущих параграфах теория напряжений и теория деформаций позволяют охарактеризовать статическую и геометрическую стороны процесса деформирования любой сплошной среды. При малых перемещениях и деформациях эти две теории не связаны между собой и потому не могут быть использованы для решения физических задач теории упругости до тех пор, пока не будет установлена зависимость между напряжениями и деформациями. Эта зависимость является математическим выражением физического закона процесса деформирования, призванного связать разнородные признаки изучаемого явления — статику и кинематику.

Ближайшая наша цель — изучение физической стороны процесса деформирования линейно-упругих тел, основное содержание которой составляет зависимость между напряжениями и деформациями в форме обобщенного закона Гука.

Общая связь между напряжениями и деформациями в упругих телах. Упругие тела после устранения внешних воздействий возвращаются в исходное (недеформированное) состояние; иначе — процесс деформирования упругих тел всегда обратим.

Аналитически это можно выразить общими зависимостями вида

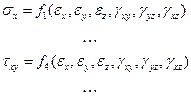(1.22)

которые в каждой точке рассматриваемого деформируемого тела устанавливают взаимно-однозначное соответствие между напряжениями и деформациями и, следовательно, однозначно разрешимы относительно последних

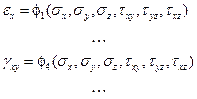
Согласно гипотезе о естественном состоянии тела все функции 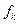, ( 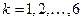) обращаются в нуль при нулевых значениях их аргументов.

При малых деформациях выражения 1.22 можно заменить их линейными аппроксимациями

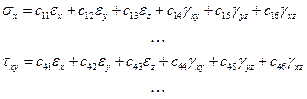(1.23)

получаемыми путем разложения в ряд Тэйлора соответствующих функций в окрестности недеформированного состояния с последующим удержанием линейных членов. Смысл величин 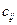( 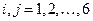) вытекает из описанной процедуры. Например,

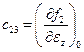
где значок “0” указывает на то, что значение частной производной берется в недеформированном состоянии, когда все деформации обращаются в нуль.

Величины 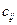характеризуют упругие свойства тела и носят название упругих постоянных. Слово "постоянные" здесь следует понимать в том смысле, что названные ими величины не зависят от деформаций и напряжений, но могут, вообще говоря, зависеть от пространственных координат.

Линейные зависимости (1.23) носят название обобщенного закона Гука (в отличии от закона Гука в теории растяжения–сжатия стержней или в теории чистого сдвига). По своему существу они формулируют закон независимости действия (принцип суперпозиции) для напряжений, предполагающий, что, например, напряжение 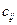, возникающее при наличии нескольких деформаций, равно сумме напряжений, возникающих от каждой деформации в отдельности.

По упругим свойствам деформируемые тела можно разделить неоднородные и однородные, изотропные и анизотропные. В однородных телах упругие свойства не зависят от рассматриваемой точки. Математически это выражается в том, что упругие постоянные 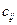не зависят от координат. Тело называется изотропным, если его упругие свойства в каждой точке не зависят от направления (рассматриваемой системы координат). Однородное или неоднородное тело может быть, в свою очередь, изотропным или анизотропным.

В природе нет идеально однородных и изотропных тел, но есть много важных с технической точки зрения материалов, которые в известном приближении можно считать однородными и изотропными. Так, например, металлы состоят из различных неизотропных частиц (кристалликов), беспорядочно расположенных друг относительно друга. Эта хаотичность в строении приводит к тому, что эти материалы ведут себя в среднем (в статистическом смысле) как однородные и изотропные.

Следует еще заметить, что тело, изотропное и однородное относительно одних свойств, может быть анизотропным и неоднородным в отношении других. В дальнейшем ограничимся рассмотрением, главным образом, изотропных и однородных тел, понимая под этим однородность и изотропность в смысле упругих свойств. Математически это выразится в том, что коэффициенты 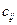в формулах (1.23) не будут зависеть от ориентации осей координат и положения рассматриваемой точки в теле.

Установлению обобщенного закона Гука предпошлем некоторые вспомогательные результаты.

1.5.1. Потенциал напряжений. Ограничиваясь рассмотрением процессов деформирования без тепловых эффектов, примем деформации за независимые параметры состояния деформируемого тела. Тогда потенциальная энергия деформированного тела

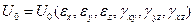
Для краткости будем писать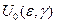

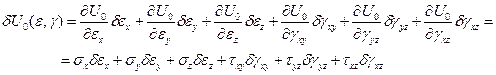
Отсюда находим

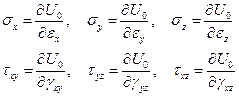(1.24)

Эти формулы носят название формул Грина и показывают, что потенциалом напряжений является плотность потенциальной энергии деформации.

В случае линейно-упругого тела согласно (1.23) все частные производные от 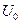являются линейными и однородными многочленами первой степени относительно деформаций. Отсюда можно сделать заключение: 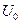есть однородный многочлен второй степени относительно тех же величин, то есть, если 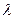— некоторый числовой параметр, то

(1.25)

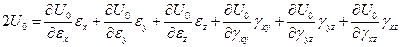
или с учетом формул Грина

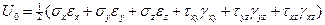(1.26)

Полученное соотношение носит название формулы Клапейрона.

1.5.2. Потенциал деформаций. В рамках допущений предыдущего пункта примем теперь действующие в теле напряжения за независимые параметры состояния деформируемого тела. Имеем

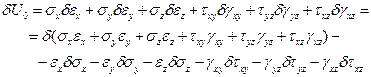
и далее

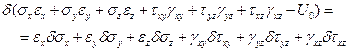(1.27)

Это выражение показывает, что функция

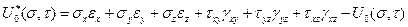, (1.28)

называемая плотностью дополнительной потенциальной энергии деформации, является полным дифференциалом своих аргументов, причем

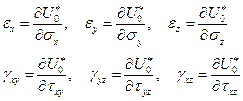(1.29)

Эти соотношения известны под названием формул Кастильяно. Они показывают, что дополнительная потенциальная энергия единицы объема является потенциалом деформаций.

Если тело линейно-упругое, то из формулы Клапейрона и выражения (1.29) следует

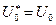(1.30)

и формулы Кастильяно приобретают вид

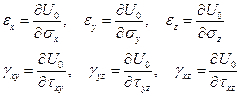(1.31)

1.5.3. Обобщенный закон Гука для однородного изотропного тела.В уравнения обобщенного закона Гука (1.23) входит, вообще говоря, 36 упругих констант. Для однородного тела они не зависят от координат 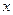, , 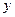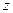. Из существования потенциала напряжений (см. (1.22), (1.23)) и независимости значения второй производной функции от порядка дифференцирования следует, что упругие постоянные, расположенные симметрично относительно главной диагонали, попарно равны между собой.

Таким образом, число упругих постоянных сокращается до 21.

Воспользуемся теперь свойством изотропии материала — независимостью его упругих свойств от выбранной системы координат — и покажем, что число независимых упругих постоянных равно двум:

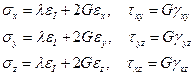(1.32)

Напомним, что 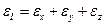— объемная деформация,

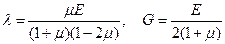(1.33)

Нетрудно показать, что обратная форма обобщенного закона Гука имеет вид

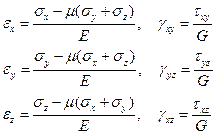(1.34)

Физически очевидно, что 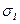и 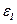всегда имеют одинаковый знак (при всестороннем сжатии, например, не может увеличиваться объем). Поэтому 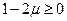и, следовательно, 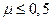. Для большинства металлов .

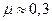1.5.4. Температурные напряжения. Раздел теории упругости, изучающий процессы деформирования нагретых упругих тел, называется термоупругостью. В общей постановке задачи термоупругости — связанные и должны решаться с учетом тепловых явлений, как в самом теле, так и во взаимодействии его с окружающей средой. Мы ограничимся рассмотрением несвязанной термоупругости, предполагающей присутствие в теле заданного поля температур, обеспечиваемого необходимыми процессами в окружающей среде (теплоотдачей) и в теле (теплопроводностью) При таких предположениях температура может выступать лишь как параметр состояния деформируемого тела.

Пусть 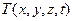— изменение температуры тела в точке 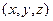в момент времени 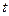отсчитываемое от некоторой начальной, постоянной для всего тела, температуры 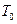. В соответствии со сказанным выше 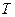удовлетворяет уравнению теплопроводности, начальным и граничным условиям. Рассмотрим малый объем тела в форме с ребрами, параллельными выбранным осям координат. В пределах объема этого параллелепипеда температуру 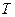можно считать постоянной. Пусть 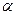— коэффициент линейного температурного расширения, одинаковый во всех направлениях (тело изотропное). Если бы параллелепипед был свободен, то за счет нагрева до температуры 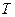он превратился бы в новый параллелепипед, размеры которого вдоль осей увеличились за счет деформаций удлинения 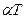одинаковых по всем направлениям. Деформации бы сдвига при этом отсутствовали.

Однако свободному расширению параллелепипеда препятствуют окружающие его части тела, что вызывает появление упругих деформаций.

В основу несвязанной термоупругости положена гипотеза Дюгамеля-Неймана, состоящая в том, что напряжения в термоупругом теле связаны с упругими деформациями обычными соотношениями обобщенного закона Гука, а полные деформации (сумма упругих и температурных) выражаются через компоненты упругого смещения обычными соотношениями Коши. На основании этой гипотезы можно записать (см. (1.17), (1.34))

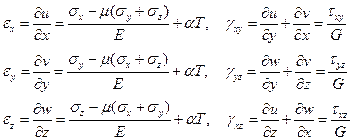(1.35)

Если разрешить эту систему относительно напряжений, то получим

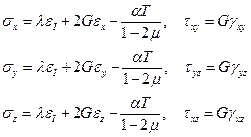(1.36)

Таким образом, в термоупругой несвязанной задаче учет температурного воздействия формально сводится к замене обычных уравнений обобщенного закона Гука (1.37). (1.34) зависимостями (1.35). (1.36) соответственно.