Геометричний зміст визначеного інтеграла

Криволінійною трапецією називається фігура, обмежена графі­ком невідʼємної неперервної функції у = f(x) на відрізку [а; b], прямими x = а, х = b і віссю .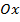

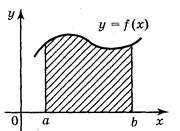
Площа криволінійної трапеції обчислюється за формулою: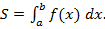

Формула Ньютона-Лейбніца є правилом обчислення визначених інтегралів: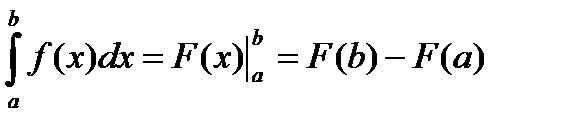

26. Елементи комбінаторики. Формули для обчислення числа перестановок, розміщень і комбінацій.

Комбінаторика– це розділ математики, в якому вивчаються питання про те, скільки різних комбінацій можна скласти з скінченого числа елементів за деяким правилом.

Групи, утворені з деяких елементів, називаються сполуками. Розрізняють три основні види сполук: перестановки, розміщення і комбінації.

Перестановками з n елементів називаються такі сполуки з усіх n елементів, які відрізняються одна від одної порядком розташування елементів.

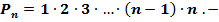кількість перестановок з n елементів дорівнює добутку послідовних натуральних чисел від 1 до n включно.

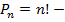«n – факторіал»

Розміщенням з n елементів по 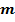називається будь – яка впорядкована підмножина з 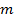елементів даної множини, яка містить n елементів; тобто розміщення – це всі 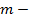елементні підмножини, які відрізняються одна від одної або складом елементів, або порядком їх розташування.

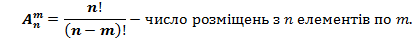
Комбінацією з n елементів по 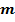називається будь – яка підмножина з 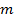елементів даної множини, яка містить n елементів; тобто комбінації – це такі сполуки, які відрізняються одна від одної тільки складом елементів.

27. Основні поняття теорії ймовірностей. Класичне означення ймовірностей.

Розділ математики, який вивчає закономірності масових випадкових подій, називається теорією ймовірностей.

Первісним поняттям теорії ймовірностей є поняття події. Подія – це явище, про яке можна сказати, що воно відбувається чи не відбувається за певних умов. Випробування – це умови, в результаті яких відбувається (чи не відбувається) подія.

Випадковою подією називається подія, яка може відбутися або не відбутися під час здійснення певного випробування. Випадкові події можуть бути масовими та одиничними. Масовими називають події, що спостерігаються за певних умов, які можуть бути відтворені необмежену кількість разів. Теорія ймовірностей вивчає лише масові випадкові події.

Вірогідною називається подія, яка внаслідок даного випробування обов’язково відбудеться (позначається Е).

Неможливою називається така подія, яка внаслідок даного випробування не може відбутися (позначається U).

Рівноможливі події – це такі події, кожна з яких не має ніяких переваг у появі частіше за іншу під час багаторазових випробувань, що проводяться за однакових умов. Попарно несумісні події – це події, дві з яких не можуть відбутися разом.

Ймовірність випадкової події – це відношення числа подій, які сприяють цій події, до загальної кількості всіх рівноможливих несумісних подій:

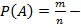класичне означення ймовірності

Ймовірність вірогідної події дорівнює 1. Ймовірність неможливої події дорівнює 0.

.
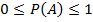