Экстремум функции

Рассмотрим 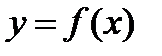(рис. 9).

Рисунок 9 – График функции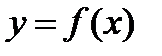

Значение функции , как справа, так и слева. Точки , точки максимума, , – точки минимума.

Функция 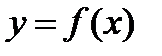имеет максимум в точке , если существует окрестность точки для любых , не равных , принадлежащих окрестности:

.

Функция 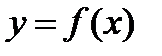имеет минимум в точке , если существует окрестность точки для любых , не равных , принадлежащих окрестности:

.

Максимум, минимум – экстремумы функции. Если максимум, то это не означает, что наибольшее значение.

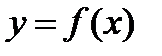Теорема (необходимый признак существования экстремума функции). Если дифференцируемая в точке функция имеет в этой точке максимум или минимум, то .

Доказательство. Функция 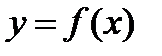имеет в точке максимум, следовательно, существует окрестность точки для любых , принадлежащих окрестности, что . Так как дифференцируема, то есть , которая по теореме Ферма равна нулю, то есть .

Для минимума доказательство аналогичное.

Может случиться, что в точке экстремума производных не существует.

Пример 1. Рассмотрим функцию (рис. 10).

Рисунок 10 – График функции

При нет производной, но при имеет место минимум.

Дополним: если непрерывная функция 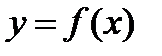имеет в точке экстремум, то при или не существует. Это условие ( не существует) является необходимым, но не достаточным.

Пример 2. Рассмотрим функцию , она имеет производную при , однако, в этой точке экстремума нет (рис. 11).

Рисунок 11 – График функции

Значение аргумента , при котором производная обращается в нуль или терпит разрыв (в частности равна бесконечности), называется критическим (критическая точка).

Теорема (достаточный признак существования экстремума). Если непрерывная функция 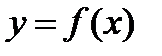имеет производную во всех точках некоторого интервала, содержащего критическую точку (за исключением может быть самой), и если при переходе аргумента слева направо через критическую точку меняет знак с плюса на минус, то в точке максимум, а при перемене знака с минуса на плюс, минимум.

Доказательство. Точка – критическая точка, пусть знак меняется с плюса на минус. Это означает, что существует , такое, что (рис. 12).

Рисунок 12 –

и .

На основании теорем о возрастании и убывании функции следует, что возрастает на и убывает на . Следовательно, будет иметь значение большее, чем значение функции во всех точках , то есть точка – максимум.

Аналогично для минимума.

Пример 3. Исследовать на наличие экстремумов функцию .

Решение. , , (рис. 13).

	+		–		+