Метод средней точки (поиск Больцано)

Если функция 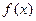унимодальна в заданном интервале поиска, то точкой оптимума является точка, в которой 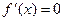. Если при этом есть возможность вычислять как значения функции, так и ее производной, то для нахождения корня уравнения 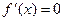можно воспользоваться эффективным алгоритмом исключения интервалов, на каждой итерации которого рассматривается лишь одна пробная точка. Например, если в точке Z выполняется неравенство , то с учетом предположения об унимодальности естественно утверждать, что точка минимума не может находиться левее точки z, то есть интервал x ≤ Z подлежит исключению. С другой стороны, если , то точка минимума не может находиться правее Z, то есть интервал x ≥ Z можно исключить. Приведенные рассуждения лежат в основе логической структуры метода средней точки, который иногда называют поиском Больцано.

Определим две точки , в которых производные имеют разные знаки: , . Искомая стационарная точка находится между ними. Найдем среднюю точку Z интервала [ ] и вычислим значение производной функции в этой точке:

.

Если то исключаем интервал , если то исключаем интервал . Ниже дается формализованное описание основных шагов алгоритма.

Пусть имеется ограниченный интервал и задан параметр сходимости e.

1. Положить

2. Вычислить

3. Если , то закончить поиск. В противном случае, если , то положить L = Z и перейти к шагу 2. Если , положить R = Z и перейти к шагу 2.

Следует отметить, что логическая структура поиска в соответствии с изложенным методом исключения интервалов основана лишь на исследовании знака производной независимо от значений, который эта производная принимает.

Метод секущих

Метод секущих является комбинацией метода Ньютона и общей схемы исключения интервалов и ориентирован на нахождение решения уравнения 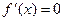на заданном интервале . Пусть в процессе поиска стационарной точки функции 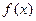на интервале обнаружены две точки , в которых знаки производных различны. В этом случае алгоритм метода секущих позволяет аппроксимировать функцию 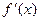секущей и найти точку, в которой секущая 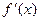пересекает ось абсцисс (см. рис. ниже). Таким образом, следующее приближение к стационарной точке определяется по формуле:

.

Если , поиск следует закончить. В противном случае необходимо выбрать одну из точек таким образом, чтобы знаки производной в этой точке и точке Z были различны, а затем повторить основной шаг алгоритма.

В отличие от метода средней точки метод секущих использует информацию не только о знаке производной, но и о ее значениях в пробных точках и поэтому в ряде случаев позволяет исключить более половины интервала поиска.

Метод секущих

.