Определение ускорения свободного падения при помощи математического маятника
(для студентов зооинженерного, ветеринарного, агрономического факультетов и факультета лесного и лесопаркового хозяйства)
Порядок выполнения работы
1. Измерить длину нити при помощи линейки с точностью до 1–5 мм. Указать погрешность измерения Dl.
2. Отклонить математический маятник на небольшой угол (не более 100) и с помощью электросекундомера измерить время десяти полных колебаний маятника (см. рис. 4). Опыт повторить не менее 5–ти раз. Полученные результаты занести в таблицу 1.
3. Рассчитать погрешность измерения времени Dt по общим правилам определения погрешностей измерений, которые приведены в приложении (в конце руководства). Результаты вычислений занести в таблицу 1.
4. Вычислить период колебаний математического маятника по формуле: 
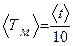и его абсолютную погрешность по формуле: 
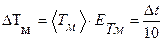. Результаты вычислений занести в таблицу 1.
5. Вычислить ускорение свободного падения, подставив длину нити l и период колебаний математического маятника Тм в формулу: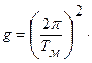 
l.
Результаты вычислений занести в таблицу 2.
6. Вычислить погрешность вычисления ускорения по формулам:
|
, 
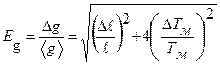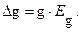
Здесь Dl – погрешность измерительной линейки (цена наименьшего деления шкалы линейки), DTм – погрешность измерения периода колебаний математического маятника.
Все результаты занести в таблицу 2.
8. Округлив полученные результаты, записать ответ по форме:
Ответ: ускорение свободного падения равно: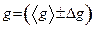 
× ед. измерения.
Пример. Ответ: масса груза равна: m = (102,5 ± 0,1)×г.
Таблица 1 Измерение времени колебаний математического маятника
| № опыта | ti, c | Dti, с | (Dti)2, с2 | Данные и результат |
| a = tna = | ||||
| l= Dl = | ||||
| Dt = Еt = | ||||
| st = | ||||
| Tм = <Tм> ±DTм | ||||
| n(n-1)= | <t>= | Dtp= | Snt= | ЕTм = Еt = |
Таблица 2 Определение ускорения свободного падения
| g, м/c2 | Dg, м/c2 | Еg | g ± Dg, м/c2 |
ЗАДАНИЕ №2
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ ПРИ ПОМОЩИ ОБОРОТНОГО ФИЗИЧЕСКОГО МАЯТНИКА
(для студентов факультетов механизации и электрификации с/х)
Порядок выполнения работы
1. Подвесить физический маятник на одну из опорных призм, установив его в кронштейн (2) так, чтобы остриё призмы встало в пазы кронштейна (см. рис. 3). Отклонить физический маятник на небольшой угол (примерно 5–60) и с помощью электросекундомера измерить время десяти полных колебаний маятника t1. Опыт повторить не менее 5–ти раз. Полученные результаты занести в таблицу 3.
2. Вычислить погрешность измерения времени Dt1 по общим правилам, которые приведены в конце руководства. Полученные результаты занести в таблицу 3.
Таблица 3 Измерение времени колебаний физического маятника
| № опыта | t1i, c | Dt1i, c | (Dt1i)2, c2 | Данные и результат |
| a = tna = | ||||
| Dt1 = Еt1 = | ||||
| st = d1 = Dd1 = | ||||
| T1 = T1 ± DT1 | ||||
| ЕT1 = Еt1 = | ||||
| n(n-1)= | <t1>= | Dt1p= | Snt1= |
3. Подвесить маятник оборотной стороной, т.е. за другую опорную призму и с помощью электросекундомера измерить время десяти полных колебаний оборотного маятника t2. Опыт повторить не менее 5–ти раз. Полученные результаты занести в таблицу 4.
4. Вычислить погрешность измерения времени Dt2 по общим правилам, которые приведены в конце руководства. Полученные результаты занести в таблицу 4.
Таблица 4. Измерение времени колебаний оборотного маятника
| № опыта | t2i, c | Dt2i, c | (Dt2i)2, c2 | Данные и результат |
| a = tna = | ||||
| Dt2 = Еt2 = | ||||
| st = d2 = Dd2 = | ||||
| T2 = T2 ± DT2 | ||||
| ЕT2 = Еt2 = | ||||
| n(n-1)= | <t2>= | Dt2p= | Snt2= |
5. Вычислить период колебаний физического и оборотного физического маятника по формуле: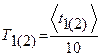 
.
Результаты вычислений занести в таблицы 3 и 4.
6. Вычислить абсолютную погрешность периода колебаний по формуле: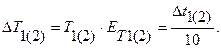 
Полученные результаты занести в таблицы 3 и 4.
8. Снять физический маятник с кронштейна и определить положение его центра масс, уравновешивая маятник на ребре призмы. Измерить миллиметровой линейкой расстояния d1 и d2 от центра масс до точек подвеса. Указать погрешность измерения расстояний. Результаты занести в таблицы 3 и 4.
9. Вычислить ускорение свободного падения, подставив полученные результаты измерения расстояний d1 и d2 и вычисления периода колебаний физического и оборотного физического маятника Т1 и Т2 в формулу:
.
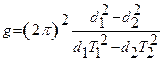Результаты вычислений занести в таблицу 5.
Таблица 5 Вычисление ускорения свободного падения
| g, м/c2 | Dg, м/c2 | Еg | g ± Dg, м/c2 |
10. Вычислить погрешности ускорения свободного падения по формулам: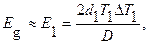 
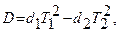если 
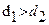(12); 
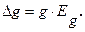Полученные результаты занести в таблицу 4.
Примечание:
Полная погрешность ускорения содержит, вообще говоря, вклады четырёх погрешностей, соответствующих непосредственно измеряемым величинам Т1, Т2, d1, d2: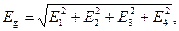 
где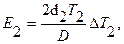 
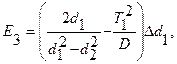
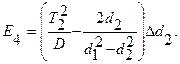
Если все измерения этой работы произведены с указанной в руководстве точностью, то погрешность (формула 12) оказывается преобладающей, она заметно больше всех других и почти полностью определяет результирующую погрешность. Проверка этого может быть сделана в качестве дополнительного упражнения.
11. Округлив полученные результаты, записать ответ по форме:
Ответ: ускорение свободного падения равно: 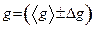× ед. измерения.
Пример. Ответ: скорость движения автомобиля равна: v = (70,0 ± 0,1)×км/ч.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется ускорением свободного падения?
2. От чего зависит ускорение свободного падения?
3. Какой маятник называется математическим, физическим?
4. Написать формулу периода колебаний математического маятника.
5. Вывести формулу периода колебаний физического маятника.
ЛИТЕРАТУРА
1. Савельев И.В. Курс общей физики. 1982. т.1
2. Зисман Г.А., Тодес О.М. Курс общей физики. 1977, т.1
3. Грабовский Р.И. Курс физики. 1980, ч.2
Приложение