Тема № 7 Эконометрическое моделирование с помощью MS Excel

Задания

Необходимо выполнить разобранные примеры на компьютере

Пример 3.

В предыдущем примере коэффициент детерминации R² равен 0,996544 (см. ячейку G6 в результатах функции ЛИНЕЙН), что указывает на сильную зависимость между независимыми переменными и ценой. Определить, является ли этот результат (с таким высоким значение R²) случайным, используя F-статистику. (СРСП тема )

Выполнение

Предположим, что на самом деле нет взаимосвязи между переменными, а просто были выбраны редкие 11 образцов зданий, для которых статистический анализ вывел сильную взаимозависимость.

Величина a используется для обозначения вероятности ошибочного вывода о том, что имеется сильная взаимозависимость.

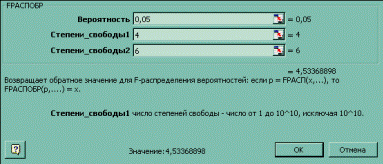
Если F-наблюдаемое больше, чем F-критическое, то взаимосвязь между переменными имеется. F-критическое можно получить из таблицы F-критических значений в любом справочнике по математической статистике. Для того, чтобы найти это значение, используя односторонний тест, положим a = 0,05, а для числа степеней свободы (обозначаемых обычно n₁ и n₂), положим n₁ = m = 4 и n₂= n - (m + 1) = 11 - (4 + 1) = 6, где m - это число переменных, а n - число точек данных.

F_{кр, a=0,05} = 4,53. Значение F_{кр, a} можно определить с использованием функции FРАСПОБР с аргументами (a, n₁, n₂).

Наблюдаемое F-значение равно 432,4997 (ячейка G7), что заметно больше чем F-критическое значение 4,53. Следовательно, полученное регрессионное уравнение полезно для предсказания оценочной стоимости зданий в данном районе.

Проверка значимости оценок коэффициентов регрессии. Статистика Стьюдента.

Величины y_i, соответствующие данным x_i являются случайными, следовательно, случайными являются и рассчитанные по ним значения коэффици­ентов b₀ и b₁. Очевидно, чем больше разброс значений у вокруг линии регрессии, тем больше (в среднем) ошибка в определении наклона линии регрессии. Формально значимость оцененного коэффициента регрессии b₁ может быть проверена с помощью анализа его отношения к своему стандартному отклонению. Эта величина в случае вы­полнения исходных предпосылок модели имеет t-распределение Стьюдента с (n-2) степенями свободы (n - число наблюдений). Она называется t-статистикой:

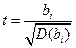
Для t-статистики проверяется нулевая гипотеза, то есть гипотеза о равенстве ее нулю. Очевидно, t= 0 равнозначно a_i = 0, поскольку t пропорциональна a_i.

Вычисление t-статистики

Пример 4. Определить, полезен ли каждый коэффициент наклона для оценки стоимости здания под офис в примере 1.

Выполнение

Для проверки того, что срок эксплуатации здания имеет статистическую значимость, разделим -0,23181 (коэффициент наклона для срока эксплуатации здания G4) на 0,013728 (оценка стандартной ошибки для коэффициента времени эксплуатации из ячейки G5). Ниже приводится наблюдаемое t-значение:

t = a₄/s₄ = -16,8862

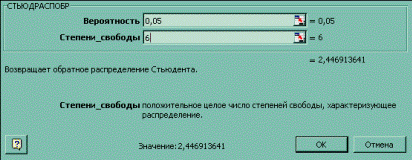
Если посмотреть полученный результат с табличным, то окажется, что t-критическое с 6 степенями свободы и Альфа = 0,05 равно 2,446914.

Для расчета можно использовать статистическую функцию СТЬЮДРАСПОБР с аргументами a=0,05 и n=6

Поскольку абсолютная величина t, равная 16,8862, больше, чем 2,446914, срок эксплуатации - это важная переменная для оценки стоимости здания под офис. Аналогичным образом можно протестировать все другие переменные на статистическую значимость. Ниже приводятся наблюдаемые t-значения для каждой из независимых переменных:

Переменная t-наблюдаемое значение

Общая площадь 4,550116

Количество офисов 30,48368

Количество входов 4,934162

Срок эксплуатации -16,8862

Окно диалога функции СТЬЮДРАСПОБР()

Все эти значения имеют абсолютную величину большую, чем 2,446914; следовательно, все переменные, использованные в уравнении регрессии, полезны для предсказания оценочной стоимости здания под офис в данном районе.

Тема №9Изучение взаимосвязей непараметрическими методами

Задача 1

Зависимость балльной оценки проектов на озеленение территории Х и стоимости работ по реализации проекта У представлена последовательностью рангов:

Rx
Ry

Рассчитайте коэффициенты корреляции Спирмена и Кендалла.

Задача 2

Связь между доходами семьи Х, расходами Z и накоплениями Y представлена ранжировками.

Rx
Ry
Rz

Определите степень тесноты связи. При уровне значимости 1 % проверить гипотезу об отсутствии ранговой множественной связи.

Рекомендуемая литература:5,6,13,14,21,26

Тема № 10Множественная линейная регрессия

Задача 1

По данным, представленным в таблице изучается зависимость индекса человеческого развития у от переменных:

х₁, - ВВП 1997 г., % к 1990 г.;

х₂ - расходы на конечное потребление в текущих ценах, % к ВВП;

х₃ - расходы домашних хозяйств, % к ВВП;

х₄ - валовое накопление, % к ВВП;

х₅ - суточная калорийность питания населения, ккал на душу населения;

х₆-ожидаемая продолжительность жизни при рождении 1997г.число лет.

Таблица

Страна	у	х1	х2	х3	х4	х5	х6
Австрия	0,904	115,0	75,5	56,1	25,2		77,0
Австралия	0,922	123,0	78,5	61,8	21,8		78,2
Белоруссия	0,763	74,0	78,4	59,1	25,7		68,0
Бельгия	0,923	111,0	77,7	63,3	17,8		77,2
Великобритания	0,918	113,0	84,4	64,1	15,9		77,2
Германия	0,906	110,0	75,9	57,0	22,4		77,2
Дания	0,905	119,0	76,0	50,7	20,6		75,7
Индия	0,545	146,0	67,5	57,1	25,2		62,6
Испания	0,894	113,0	78,2	62,0	20,7		78,1
Италия	0,900	108,0	78,1	61,8	17,5		78,2
Канада	0,932	113,0	78,6	58,6	19,7		79,0
Казахстан	0,740	71,0	84,0	71,7	18,5		67,6
Китай	0,701	210,0	59,2	48,0	42,4		69,8
Латвия	0,744	94,0	90,2	63,9	23,0		68,4
Нидерланды	0,921	118,0	72,8	59,1	20,2		77,9
Норвегия	0,927	130,0	67,7	47,5	25,2		78,1
Попьша	0,802	127,0	82,6	65,3	22,4		72,5
Россия	0,747	61,0	74,4	53,2	22,7		66,6
США	0,927	117,0	83,3	67,9	18,1		76,7
Украина	0,721	46,0	83,7	61,7	20,1		68,8
Финляндия	0,913	107,0	73,8	52,9	17,3		76,8
Франция	0,918	110,0	79,2	59,9	16,8		78,1
Чехия	0,833	99,2	71,5	51,5	29,9		73,9

Задание

1.Постройте матрицу парных коэффициентов корреляции. Рассчитайте коэффициенты множественной детерминации, используя в зависимой переменной каждый фактор. Установите, какие факторы мультиколлинеарны.

2. Постройте уравнение множественной регрессии в линейной форме с полным набором факторов.

3.Оцените статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.

4. Отберите информативные факторы по пп.1 и 3. Постройте уравнение регрессии со статистически значимыми факторами.

Рекомендуемая литература:5,6,13,14,21,26

Тема №11Анализ временных рядов

Задача 1

Имеются данные об урожайности зерновых в хозяйствах области:

Год Урожайность зерновых, ц/га

1 10,2

2 10,7

3 11,7

4 13,1

5 14,9

6 17,2

7 20,0

8 23,2

Задание

1 . Обоснуйте выбор типа уравнения тренда.

2. Рассчитайте параметры уравнения тренда.

3. Дайте прогноз урожайности зерновых на следующий год.

Задача 2

Имеются следующие данные об уровне безработицы у( (%) за 8 месяцев:

месяцы
уt	8,8	8,6	8,4	8,1	7,9	7,6	7,4	7,0

Задание

1 . Определите коэффициенты автокорреляции уровней этого ряда первого и второго порядка.

2. Обоснуйте выбор уравнения тренда и определите его параметры.

3. Интерпретируйте полученные результаты.

Задача 3

Пусть имеется следующий временной ряд:

t
xt		…	…	…	…	…	…

Известно также, что ∑x_t = 150, ∑x_t²=8100, ∑x_t x_t-1 = 7350

Задание

1. Определите коэффициент автокорреляции уровней этого ряд первого порядка.

2. Установите, включает ли исследуемый временной ряд тенденцию.

Задача 4

Годовое потребление товара А и доходы населения (тыс.тенге.) за 1989-1997 гг. приведены в таблице.

Таблица

Показатель	1989.
Потребление
Доходы

Задание

1. Определите уравнение регрессии, включив в него фактор времени, если известно, что ∑Ү = 599, ∑Х = 731, ∑УХ = 52179, ∑Х² = 64361,∑У² =42367.

2, Интерпретируйте полученные результаты.

Задача 5

В таблице приводятся данные об уровне дивидендов, выплачиваемых по обыкновенным акциям (в процентах), и среднегодовой стоимости основных фондов компании (X, млн тенге.) в сопоставимых ценах за последние девять лет.

Показатель
Среднегодовая стоимость основных фондов
Дивиденды по обыкновенным акциям	4,2	3,0	2,4	2,0	1,9	1,7	1,8	1,6	1,7

Задание

1. Определите параметры уравнения регрессии по первым разностям и дайте их интерпретацию. В качестве зависимой переменной используйте показатель дивидендов по обыкновенным акциям.

2. В чем состоит причина построения уравнения регрессии по первым разностям, а не по исходным уровням рядов?

Рекомендуемая литература:5,6,13,14,21,26