Ранг и базис системы векторов

Линейные пространства

Понятие линейного пространства

Определение. Множество Z называется линейным пространством, а его элементы векторами, если:

а) задан закон (операция сложения), по которому любым двум элемен-

там и из сопоставляется элемент, называется их суммой и обозначается

+ ;

б) задан закон (операция умножения на число), по которому элементу

из и числу α сопоставляется элемент из Z, называемый произведением

на α и обозначается α ;

в) для любых элементов , , из и любых чисел α и β выполне­ны

следующие требования (аксиомы):

1. + = +

2. ( + ) + = + ( + )

3. Существует элемент такой, что для каждого из выполнено ра­венство + 0 =

4. Для каждого уществует элемент такой, что + ( - )= .

5. α( + ) = α + α .

6. (α + β) х = α + β .

7. α (β ) =( α β) .

8. 1· = .

Примеры линейных пространств:

1. Множество свободных векторов геометрического пространства которые складываются и умножаются на число по обычным правилам векторной алгебры.

2. Множество всех многочленов степени не выше второй, которые скла­дываются и умножаются на число по обычным правилам алгебры.

3. Множество упорядоченных наборов чисел (строк)

= (x₁, x₂, …, x_n), если действия над строками определяются следующим образом:

+ = (x₁, x₂, …x_n) + (y₁, y₂, …y_n), = (x₁+y₁, x₂+y₂, …x_n+y_n).

α = α (x₁, x₂, …x_n) = (αx₁, αx₂, … αx_n).

Данное линейное пространство строк обозначим R_n.

Линейная зависимость и линейная независимость векторов линейного пространства

Определение. Векторы ( ₁, ₂, … _m) называются линейно«зависимыми, если существуют такие числа α₁, α₂, … α_m, из которых хотя бы одно не равно нулю, что α_{1 1}+α_{2 2}+ …+ α_{m n} = 0.

Определение. Векторы ( ₁, ₂, … _m) называются линейно независимыми, если равенство α_{1 1}+α_{2 2}+ …+ α_{m m} = возможно только при α₁ = α₂ = …α_m = 0.

Определение. Если вектор , выражается через векторы ₁, ₂, … ₃ в виде

= α_{1 1}+α_{2 2}+ …+ α_{s s}, то вектор называется линейной ком­бинацией векторов ₁, ₂, … _s

Теорема. Векторы ₁, ₂, … _m линейно зависимы тогда и только то­гда, когда хотя бы один из них является линейной комбинацией остальных.

Пусть даны га векторов пространства R_n:

₁ =( ₁₁, ₁₂, … _1n),…, _m =( _m1, _m2, … _mm). Необходимо выяснить, при

каких условиях данные m векторов линейно зависимы или линейно независимы. Рассмотрим векторное равенство:

α₁ (x₁₁, x₁₂, …x_1n) + α₂ (x₂₁, x₂₂, …x_2n) + …+ α_m (x_m1, x_m2, …x_mn) = (0; 0; 0...0). Векторное равенство равносильно системы уравнений:

Если данная однородная система имеет только нулевое

α₁ = α₂ = …α_m = 0, то векторы линейно независимы.

Систему решаем методом Гаусса.

Если система имеет ненулевое решение, то векторы линейно зависимы. Пример. Исследовать на линейную зависимость векторы

₁=(1;2;3;4;1), ₂=(2;-1;1;2;3), ₃=(3;1;4;6;4)

Решение: α₁(1;2;3;4;1) + α₂(2;-1;1;2;3) + α₃(3;1;4;6;4) = (0;0;0;0;0)

Система имеет бесконечное множество ненулевых решений. Следова­тельно, векторы линейно зависимы.

Ранг и базис системы векторов

Пусть дана система m векторов линейного пространства ₁ =( ₁₁, ₁₂, … _1n),

₂ =( ₂₁, ₂₂, … _2n), _m =( _m1, _m2, … _mm).

Определение. Базисом системы векторов называется такая ее подсистема, которая обладает следующими свойствами:

1) эта подсистема линейно независима;

2) любой вектор всей системы является линейной комбинацией векторов указанной подсистемы.

Из координат векторов составим матрицу:

По аналогии с трехмерным векторным пространством элементы любого линейного пространства называются векторами, хотя природа этих элементов может быть совсем иная.

Другими примерами вещественных линейных пространств могут служить:

1. множество столбцов из 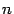элементов, являющихся вещественными числами ;

2. множество многочленов степени не выше 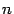с вещественными коэффициентами;

3. множество всех многочленов с вещественными коэффициентами;

4. множество функций непрерывных на некотором отрезке .

В примерах 2-4 нулевым вектором является многочлен или функция тождественно равная нулю, то есть равная нулю при всех значениях аргумента. Проверку того, что указанные множества являются линейными пространствами, предоставляем читателю.

Если в примерах 1-3 слово "вещественными" заменить на "комплексными", то получим примеры комплексных линейных пространств.

Пример 18.1 Рассмотрим еще один пример линейного пространства. Пусть имеется однородная система линейных уравнений, которую запишем в матричном ви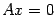де , где 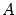-- матрица системы, а 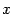-- столбец неизвестных. В силу предложения 15.3 столбцы-решения системы можно складывать и умножать на число. При этом будут получаться снова решения этой системы. Значит, на множестве решений определены операции сложения и умножения на число. Легко проверить, что эти операции удовлетворяют требованиям из определения линейного пространства. Итак, множество решений однородной системы линейных уравнений является линейным пространством. Если матрица 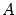имеет вещественные элементы, то и пространство будет вещественным, если комплексные -- то и пространство будет комплексным.

Наверх: Линейные пространства Назад: Линейные пространства