Вопрос 18.2. Производная функции и ее геометрический смысл
Определение 18.2. Производной функции  в точке x называется предел
в точке x называется предел
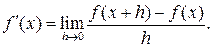
Производную функции обозначают так же через 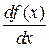 или
или 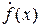 . Последнее обозначение распространено в механике.
. Последнее обозначение распространено в механике.
Определение 18.3. Правой производной функции  в точке x называется правый предел
в точке x называется правый предел
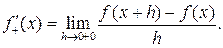
Определение 18.4. Левой производной функции  в точке x называется левый предел
в точке x называется левый предел
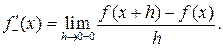
Теорема 18.1. Если в точке x существуют правая и левая производные функции и они равны между собой, то в этой точке существует производная функции, равная односторонним производным.
Теорема 18.2. Если в точке x существует производная функции, то существуют в этой точке и равные ей односторонние производные.
Доказательство этих теорем аналогично доказательству соответствующих теорем об односторонних пределах.
Геометрический смысл производной устанавливает следующая теорема (см. рис. 2)
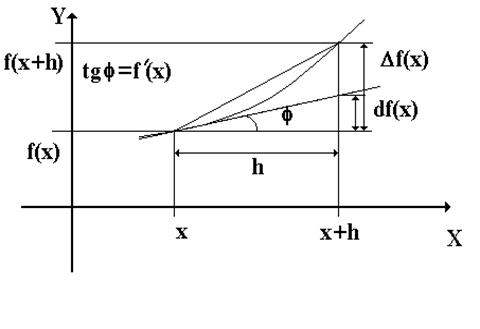
Рис. 2. Геометрический смысл производной.
Теорема 18.3. Производная функции  в точке x равна тангенсу угла наклона касательной к графику функции, проведенной в этой точке.
в точке x равна тангенсу угла наклона касательной к графику функции, проведенной в этой точке.
Докажите эту теорему самостоятельно.
Теорема 18.4. Если функция  дифференцируема в точке x, то она непрерывна в этой точке.
дифференцируема в точке x, то она непрерывна в этой точке.
Доказательство. Вычислим предел
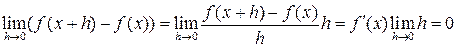 ,
,
откуда
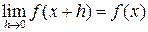
Конец доказательства.
Вопрос 18.3. Правила дифференцирования.
Если  и
и 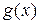 две дифференцируемые в точке x функции, то справедливы следующие правила дифференцирования:
две дифференцируемые в точке x функции, то справедливы следующие правила дифференцирования:
1) производная константы (функции, принимающей постоянные значения) равна нулю;
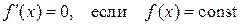 .
.
2) производная суммы двух функций  и
и 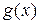 равна сумме их
равна сумме их
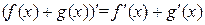
3) производная разности двух функций  и
и 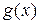 равна разности их
равна разности их
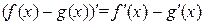
4) производная произведения двух функций  и
и 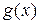 равна
равна
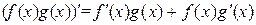
5) производная отношения двух функций  и
и 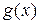 равна
равна
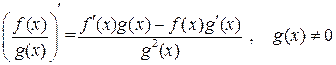 .
.
Докажите эти утверждения самостоятельно.
Вопрос 18.4. Дифференцируемость сложной и обратной функции.
Теорема 18.5. (Дифференцируемость сложной функции). Пусть функция 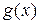 определена на интервале I и принимает значения из интервала I', а функция
определена на интервале I и принимает значения из интервала I', а функция  определена на интервале I', тогда если
определена на интервале I', тогда если 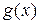 дифференцируема в точке x из интервала I, а
дифференцируема в точке x из интервала I, а  дифференцируема в точке
дифференцируема в точке 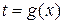 , то сложная функция
, то сложная функция 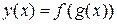 дифференцируема в точке x и
дифференцируема в точке x и
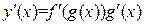 .
.
Доказательство. Согласно определению производной
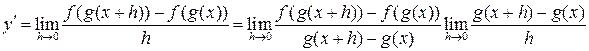
Пусть 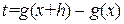 , тогда получим
, тогда получим 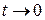 , если
, если 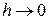 и следовательно
и следовательно
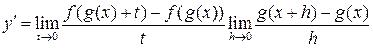
или 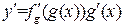 .
.
Конец доказательства.
Пример 18.2. Вычислить производную сложной функции 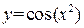 .
.
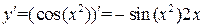 .
.
Конец примера.
Теорема 18.6. (Дифференцируемость обратной функции). Пусть 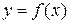 строго монотонная и непрерывная на интервале I функция, принимающая значения из интервала E. Тогда, если
строго монотонная и непрерывная на интервале I функция, принимающая значения из интервала E. Тогда, если  дифференцируема на I, то на интервале E существует дифференцируемая обратная функция
дифференцируема на I, то на интервале E существует дифференцируемая обратная функция 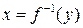 , причем
, причем
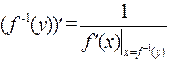 .
.
Доказательство. Из условий теоремы следует существование и единственность обратной функции 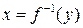 , определенной на интервале E.
, определенной на интервале E.
Тогда
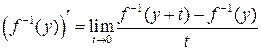 .
.
Обозначим через h разность 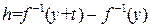 , тогда, учитывая, что
, тогда, учитывая, что 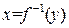 , получим
, получим 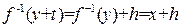 , или
, или 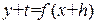 . Отсюда, учитывая, что при
. Отсюда, учитывая, что при 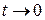
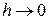 , получим
, получим
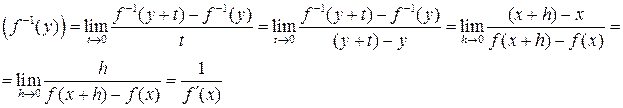 Конец доказательства.
Конец доказательства.
Пример 18.3. 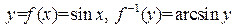
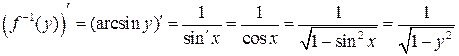
Конец примера.
