Построение дифференциальной функции теоретического закона распределения

4.6.1 Определение дифференциальной функции для ЗНР

Дифференциальную функцию или плотность вероятностей определяют по уравнению (2):

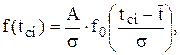(17)

где А –величина интервала;

σ – среднее квадратическое отклонение;

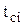– середина i-го интервала;

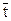– среднее значение показателя надежности;

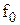– так называемая центрированная дифференциальная функция. Она табулирована и ее значение определяют по приложению А, учитывая при этом, что

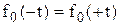. (18)

Подставляя в формулу (17) исходные данные из таблицы 3 для нашего примера: А=1500 мото-ч, σ = 2130 мото-ч, 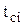= 1650 мото-ч; 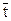= 4420 мото-ч, определим значение дифференциальной функции 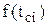для первого интервала:

.

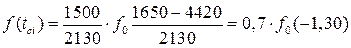Пользуясь таблицей приложения А, находим 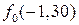=0,17. Тогда .

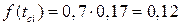Аналогично определяем значение дифференциальной функции для остальных интервалов. Результаты расчета заносим в таблицу 5.

4.6.2 Определение дифференциальной функции для ЗРВ

Дифференциальную функцию или плотность вероятностей определяют по уравнению

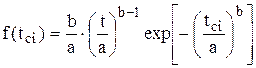, (19)

где 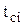– середина i-го интервала;

а – параметр ЗРВ, определяемый по формуле

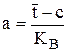, (20)

где 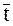– среднее значение показателя надежности;

с – сдвиг начала рассеивания показателя надежности;

К_В– коэффициент ЗРВ, определяется по приложению Е в зависимости от коэффициента вариации;

b – параметр ЗРВ. Определяется по приложению И в зависимости от V.

Для нашего примера: 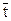=4,42 мото-ч; с = 0;V = 0,48; b = 2,2; 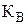= 0,89 (приложение И).

Тогда по формуле (20):

.

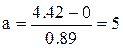Параметр «а» также можно приближенно определить по формуле

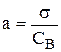, (21)

где σ – среднее квадратичное отклонение;

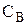–коэффициент закона распределения Вейбулла (3PB), определяется по приложению Л в зависимости от коэффициента вариации V.

Для нашего примера: V= 0,48; 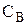= 0,425; σ = 2,13.

Тогда по формуле (12):

.

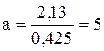Подставляя в формулу (19) полученные для нашего примера значения параметров 3PB а = 5; b = 2,2 м и величину (таблица 3), получаем значения дифференциальной функции 3PB для середины каждого интервала.

Таблица 5 – Сводная таблица опытной вероятности и теоретических законов(3HP и ЗРВ) распределений полных pecypcов двигателей

Интервал, тыс. мото-ч	Опытная Вероят-ность Pi	Дифференциаль-ная функция	Накоплен-ная вероятность ΣPi	Интегральная функция
ЗНР	ЗРВ	ЗНР	ЗРВ
0,9-2,4	0,125	0,12	0,14	0,125	0,17	0,18
2,4-3,9	0,406	0,24	0,29	0,531	0,40	0,43
3,9-5,4	0,188	0,28	0,27	0,719	0,68	0,70
5,4-6,9	0,156	0,26	0,17	0,875	0,88	0,87
6,9-8,4	0,031	0,08	0,09	0,906	0,97	0,96
8,4-9,9	0,094	0,02	0,04	1,0	1,0	1,0

Например, для первого интервала по формуле (19) имеем:

.

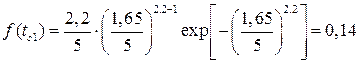Аналогично определяем значение дифференциальной функции теоретического закона распределения Вейбулла (ЗРВ) для остальных интервалов.

Используя данные таблицы 5 построим дифференциальную функцию ЗНР и ЗРВ в соответствии с рисунком 3.

При наличии интегральной функции ЗРВ дифференциальная функция 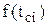в i-м интервале статистического ряда может быть получена как разность интегральных функций в конце н начале этого интервала:

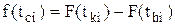, (22)

где 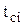, , 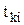,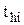— значения показателя надежности соответственно в середине, в конце и начале i-го интервала.

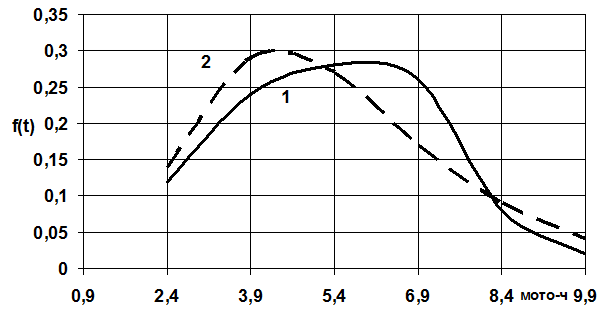
Рисунок 3 – Дифференциальная функция теоретического закона распределения 3HP (1) и ЗРВ (2) полного ресурса двигателей

Например, для второго и последующих интервалов дифференциальная функция 3PB по уравнению (22) составит:

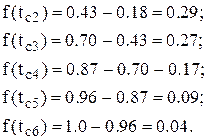
Для первого интервала значение дифференциальной функции определяется по уравнению (19) или определяется с использованием таблиц для расчета показателей надежности из приложений.