Основное уравнение динамики вращательного движения
Тема 3.Элементы механики твердого тела.
Лекция №5.
Кинематические соотношения
Определение момента силы.
Основное уравнение динамики вращательного движения.
4. Момент инерции, момент импульса твёрдого тела.
Кинематические соотношения.
Твердое тело можно рассматривать как систему материальных точек, жестко скрепленных друг с другом. Характер его движения может быть различным.
В основном различают поступательно и вращательное движения.
При поступательном движении все точки тела движутся по параллельным траекториям, так что для описания движения тела в целом достаточно знать закон движения одной точки. В частности, такой точкой может служить центр масс твердого тела
При вращательном (более сложном!)движении все точки тела описывают концентрические окружности, центры которых лежат на одной оси. Скорости точек на любой 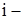 той окружности связаны с радиусами этих окружностей и угловой скоростью
той окружности связаны с радиусами этих окружностей и угловой скоростью
вращения: 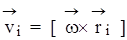 . Так как твердое тело при вращении сохраняет свою форму, радиусы вращения остаются постоянными и линейное ускорение будет равно:
. Так как твердое тело при вращении сохраняет свою форму, радиусы вращения остаются постоянными и линейное ускорение будет равно:


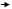
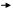
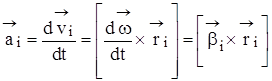 . ( 1 )
. ( 1 )
Определение момента силы.
Для описания динамики вращательного движения твердого тела необходимо ввести понятия моментов силы.
Определение 1.
Моментом – 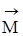 силы –
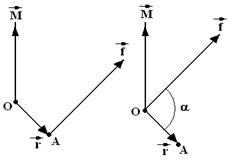
силы – 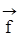 , приложенной к материальной точке т.А, относительно произвольной точки т.О называется векторное произведение радиуса-вектора
, приложенной к материальной точке т.А, относительно произвольной точки т.О называется векторное произведение радиуса-вектора 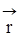 , проведенного из точки т.О к точке т.А:
, проведенного из точки т.О к точке т.А:
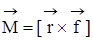 .
.
Примечание.
Модуль векторного произведения, то есть собственно величина момента, определяется произведением – 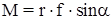 ,а направлениемомента даётся определением правой тройки векторов
,а направлениемомента даётся определением правой тройки векторов 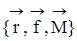 .
.
Определение 2.
Моментом – 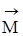 силы –
силы – 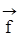 , приложенной в точке т.А, относительно произвольной оси
, приложенной в точке т.А, относительно произвольной оси 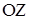 называется векторное произведение радиуса-вектора
называется векторное произведение радиуса-вектора 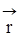 и составляющей силы
и составляющей силы 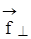 , лежащих в плоскости, перпендикулярной оси
, лежащих в плоскости, перпендикулярной оси 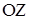 и проходящей через точку т.А:
и проходящей через точку т.А:
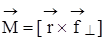 .
.
Основное уравнение динамики вращательного движения.
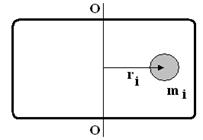
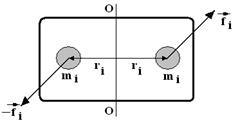
Пусть имеется твердое тело произвольной формы, которое может вращаться вокруг оси ОО . Разбивая тело на малые элементы, можно заметить, что все они вращаются вокруг оси ОО в плоскостях, перпендикулярных оси вращения с одинаковой угловой скоростью w.
Движение каждого из отдельных элементов малой массы mi описывается вторым законом Ньютона.
Для i-го элемента имеем:
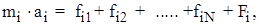 ( 1 )
( 1 )
 |
где fik ( k = 1,2, ...N) представляют собой внутренние силы взаимодействия всех
 элементов с выбранным, а Fi- равнодействующая всех внешних сил, действующих на i- элемент.
элементов с выбранным, а Fi- равнодействующая всех внешних сил, действующих на i- элемент.
Скорость vi каждого элемента вообще говоря может меняться как угодно, но поскольку тело является твердым, то смещения точек в направлении радиусов вращения можно не рассматривать. Поэтому спроектируем уравнение (1) на направление касательной к окружности вращения и умножим обе части уравнения на ri:
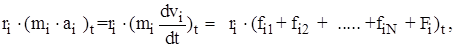 (2)
(2)
В правой части получившегося уравнения произведения типа 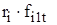 представляют собой моменты внутренних сил относительно оси вращения, т.к. riи f itвзаимно перпендикулярны. Аналогично произведения
представляют собой моменты внутренних сил относительно оси вращения, т.к. riи f itвзаимно перпендикулярны. Аналогично произведения 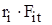 являются моментами внешних сил, действующих на i-элемент.
являются моментами внешних сил, действующих на i-элемент.
 Просуммируем в уравнении движения по всем элементам, на которые было разбито тело.
Просуммируем в уравнении движения по всем элементам, на которые было разбито тело.
Сумму моментов внутренних сил можно разбить по парам слагаемых, обязанных своим возникновением взаимодействию двух симметричных элементов тела между собой. Их моменты равны и противоположно направлены. На основании этого можно сделать вывод, что при сложении всех моментов внутренних сил они попарно уничтожатся. Суммарный момент всех внешних сил обозначим S Мi , где Mi = [ ri × Fi].
Левая часть уравнения ( 2) с учетом соотношения (1) в предыдущем разделе представляется в таком виде:
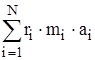 =
= 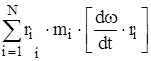 =
= 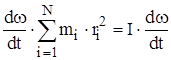 , ( 3 )
, ( 3 )
где 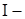 момент инерции.
момент инерции.
Уравнение (3) есть основное уравнение вращательного движения.
4.Момент инерции твёрдого тела.
Определение 1.
Величина 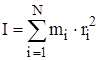 называется моментом инерции твердого тела относительно заданной оси.
называется моментом инерции твердого тела относительно заданной оси.
Эта величина характеризует распределение массы тела относительно определенной оси. Момент инерции – это величина аддитивная, то есть «суммируемая».
При практическом вычислении моментов инерции используется интегрирование.
Если ось, относительно которой вычисляется момент инерции, проходит через центр симметрии тела, то вычисление такого интеграла представляет сравнительно несложную задачу, но в общем случае задачу решить трудно.
Рассматривая правую часть основного уравнения вращательного движения (3), аналогично моменту инерции можно ввести, так называемый, момент импульса – 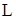 .
.
Действительно,
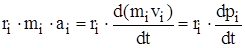 =
= 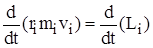 . (4)
. (4)
Определение 2.
Величина 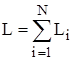 (где
(где 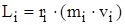 ) называется моментом импульса твердого тела относительно заданной оси.
) называется моментом импульса твердого тела относительно заданной оси.
Как следует из соотношений (3) и (4), 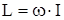 . То есть, момент импульса твёрдого тела пропорционален моменту его инерции с коэффициентом пропорциональности, равным угловой скорости вращения.
. То есть, момент импульса твёрдого тела пропорционален моменту его инерции с коэффициентом пропорциональности, равным угловой скорости вращения.
В терминах момента импульса основное уравнение вращательного движения можно переписать в виде:

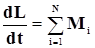 . ( 5 )
. ( 5 )
