Последствия и симптомы ошибки спецификации линейной эконометрической модели, состоящей во включении незначимой объясняющей переменной
Наличие в модели незначащих, объясняющих переменных. Опр.: Принято объясняющую переменную модели (x1) называть незначащей, если коэф при этой переменной (а1) равен 0. Незначащие переменные разумно исключить из модели, поскольку их присутствие с одной стороны увеличивает ошибки прогнозирования, а с другой – приводит к лишним затратам на измерение значений незначащий переменной.
Тест незначимости экзогенной переменной модели базируется на следующей теореме:
Пусть справедливы все предпосылки теоремы Г-М и случайный остаток имеет нормальный закон распределения. Тогда при справедливой гипотезе: Н0: а1=0, следующая дробь 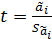 распределена по закону стьюдента с числом степеней свободы m=(n-(k+1))
распределена по закону стьюдента с числом степеней свободы m=(n-(k+1))
Следовательно тест незначимости переменной хi в модели включает следующие этапы:
1) Визуальный поиск в оцененной модели тех объясняющих переменных,для которых справедлива следующие неравенства |aj|<= 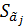
2) Вычисление статистики t критерий гипотезы H0: 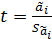
3) При заданном уровне значимости α и количестве степеней свободы m=n-(k+1) определяем число tкр
4) Проверка неравенства: |t|<=tкр
Если неравенство справедливо, то Н0 принимается и xj – интерпретируется как незначащая. Такая переменная может быть исключена из модели.
В противном случае Н0 отвергается, переменная хj объявляется значащей в моделе.
Замечание: удалять переменные следует с большой осторожностью, т.к. возможна ошибка в признании гипотезы Н0, когда она не верна и, следовательно, возможна ошибка в исключении значащей переменной. В таком случае экономист совершает очень серьезную ошибку, которая состоит в пропуске в моделе значащей переменной.
Последствия и симптомы ошибки спецификации линейной эконометрической модели, состоящей в пропуске значимой объясняющей переменной.
Эта ошибка по последствиям и симптомам эквивалентна неверному выбору типа функции регрессии. Пусть на первом этапе экономист составил спецификацию модели (1) 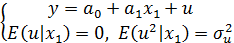 в ситуации, когда истинной является спецификация
в ситуации, когда истинной является спецификация 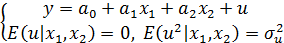 при условии, что гипотеза
при условии, что гипотеза 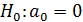 неверна. Это означает, что экономист сделал ошибочный выбор типа функции регрессии, а именно: вместо функции двух аргументов выбрал функцию одного аргумента. Влияние данной ошибки на случайный остаток в модели (1):
неверна. Это означает, что экономист сделал ошибочный выбор типа функции регрессии, а именно: вместо функции двух аргументов выбрал функцию одного аргумента. Влияние данной ошибки на случайный остаток в модели (1):
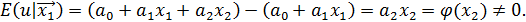
Действительно пропуск значащей объясняющей переменной эквивалентен неверному выбору типа функции регрессии. Если пропущенная переменная (скажем, регрессор 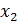 ) недоступна для наблюдений, то экономист может включить в модель ее заместителя - такую переменную
) недоступна для наблюдений, то экономист может включить в модель ее заместителя - такую переменную 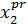 , которая доступна для наблюдений и коррелирует с переменной
, которая доступна для наблюдений и коррелирует с переменной 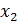 .
.
