D) матрицасынан туындаған нольге тең емес минорлардың ең жоғарғы ретін айтады

C) таңбасын өзгертеді

Егер кандай да бир жолынын элементтерин 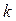санына кобейтсе, аныктауыш мани

B) 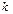-есе өседі
Егер аныктауштын еки жатык жолдарынын сайкес элементтери тен болса, онда аныктауыштын мани

D) нольге тең

Егер n -ші ретти аныктауыштын кандай да бир жатык жолына баска жатык жолдын сайкес элементтерин -га кобейтип коссак, онда аныктауыштын мани

A) өзгермейді

Егер аныктауыштын бир жатык жолы нольдик элементтерден турса, онда онын мани

E) 0

Егер аныктауыштын еки баганын орындарын ауыстырсак, онда онын мани

B) таңбасын өзгертeді

Егер аныктауштын кайсибир жолынын элементтеринин ортак кобейткиши бар болса, онда

C) оны анықтауыштың алдына шығаруға болады

Егер аныктауыштын еки баганасынын сайкес элементтери тен болса, онда ол

C) нөлге тең

Егер 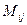аныктауыштын 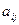элементинин миноры болса, онда осы элементтин алгебралык толыктауышы мынаган тен

E)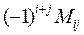

Аныктауышты есепте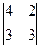

D) 6

Аныктауышты есепте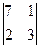

D) 19

Аныктауышты есепте

B) -11

Аныктауышты есепте

C) -5

Тендеуди шешиниз

A) -8

Тендеуди шеш

B) -2

аныктауыштын А23алгебралык толыктауышын тап

E) -20

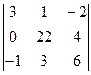аныктауыштын А32алгебралык толыктауышын тап

C) -12

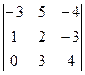аныктауыштын А12алгебралык толыктауышын тап

D) -4

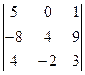аныктауыштын А23алгебралык толыктауышын тап

A) 10

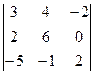аныктауыштын А31алгебралык толыктауышын тап

B) 12

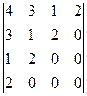аныктауышын табу

A)16

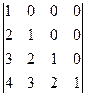аныктауышын табу

C) 1

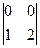аныктауышын есептеу

E) 0

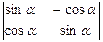аныктауышын табу

D) 1

матрицасынын аныктауышын есептеу керек

E) 13

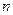-ретти 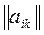квадрат матрицасы бирлик матрица делинеди, егерде

B) бас диагоналдын бойындагы барлык элементтери бирге тен, ал калган элементтери нолге тен

матрицасын санына кобейту ушин мыналар кажет:

A) матрицасынын арбир элементин санына кобейту

Бирлик матрицаны корсет

A)

Егер 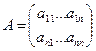матрицасынын аныктауышы нолге тен емес болса, онда матрицага кери матрица 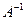мына формуламен есептеледи

C)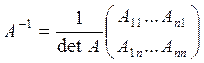

А*В табыныз, мундагы .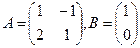

(E)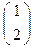

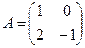матрицасынын кери матрицасын тап

D)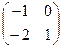

АВ тап, мундагы ;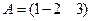

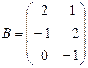
B)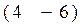

А*В тап, мундагы ;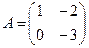

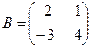
E)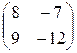

А*В тап, мундагы 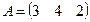жане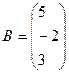

A)

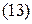
А*В тап, мундагы ;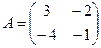

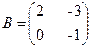
C)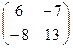

А*В тап, мундагы ;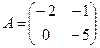

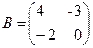
D)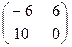

А*В тап, мундагы ;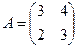

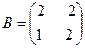
B)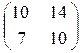

А*В тап, мундагы ;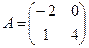

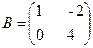
A)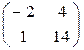

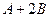тап, егер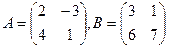

C)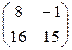

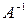матрицасы 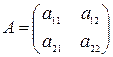матрицасынын кери матрицасы болып табылады.

Мына тужырымдардын кайсысы кате:

E) егер болса, онда матрицасынын кери матрицасы бар болады

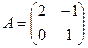матрицасынын кери матрицасын тап:

D)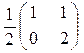

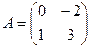матрицасынын кери матрицасын тап:

B)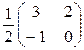

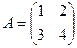матрицасынын кері матрицасын тап:

(C)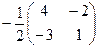

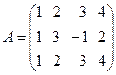матрицасы рангин табу:

A) 2

Матрицанын ранги озгермейди, егер:

E)қандай да бір жолын нольден өзгеше санға көбейтсе

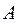матрицасынын ранги деп:

D) матрицасынан туындаған нольге тең емес минорлардың ең жоғарғы ретін айтады

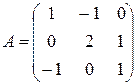матрицасы ушин кери матрицаны табу

A)

Биртекти тендеулер жуйесин шеш .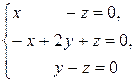

B) (0,0,0)

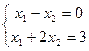жуйесин шешу

C)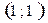

, нуктелери берилген, векторын тап

E)(2,-3,-5)

нуктелери берилген, + векторын тап

C) (1,3)

Егер , 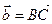болса,онда олардын косындысы томендегидей болады

D)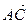

=(0;3;1) =(1;-2;1)векторлары берилген. -ны тап

B)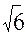

А (1,0,0), В (3,4,5),С(1,3,5) нуктелери берилсе, онда АВ+ВС векторын тап

A) (0,3,5)

А(1;0;1) В(0;2;1) С(1;-1;0) болса, АВ+ВС векторын тап

A) (0,-1,-1)

Егер 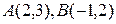болса, 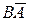векторынын координатасын табу

D) (-3,-1)

Еки вектор коллинеар болса, онда томендеги шарт орындалатын

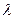саны табылады.

C)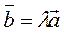

Егер 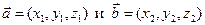, болса,онда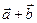

B)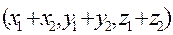

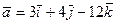векторынын ортын табу

E)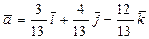

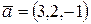векторынын бирлик векторынын ординатасын табу

C)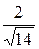

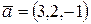векторынын бирлик векторынын аппликатасын табу

D)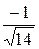

64. векторы координаталык осьтермен 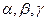суйир бурыш жасайды, мундагы 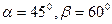, . Вектордын координаталарын табу

A)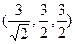

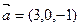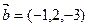, векторларынын арасындагы бурышты тап

E) 90

Векторлардын векторлык кобейтиндиси х былай орнектеледи

B)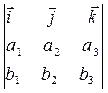

Векторлардын скаляр кобейтиндиси

A)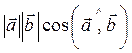

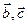векторларынын косындысынын векторына скаляр кобейтиндиси мынаган

тен:

C)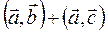

мен векторларынын коллинеарлык белгисинин кажетти жане жеткиликти шартын корсет:

A)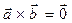

мен векторларынын векторлык кобейтиндисинин мынадай касиети бар:

E)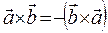

Векторлар коллинеар болады егер,олар:

B) бир немесе параллель тузулерде жатса,

D) -12

векторынын узындыгын табу, мундагы және векторлары бурыш жасайды: , .

C)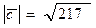

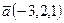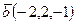, векторлары берилген, векторлык кобейтиндисин табу

A)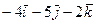

егер , болса, кобейтиндисин тап:

B)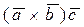

Егер векторлар компланар емес болса,онда мына шарт орындалады:

E)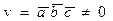

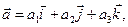
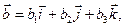
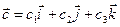
векторларынын аралас кобейтиндисин тап

D)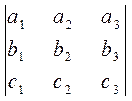

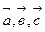векторларынын компланар болуынын кажетти жане жеткиликти шартын корсет

B)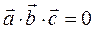

Векторлар компланар болады ,егер

A) бир жазыктыкта жатса

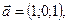
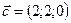болса, , есепте

D) 0

Егер тобелери О(1,1,2), А(2,3,-1), В(2,-2,4), С(-1,1,3) болса, тетраэдр колемин тап:

C)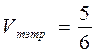

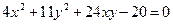кисыгы тендеуин канондык турге келтиру

A)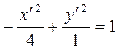

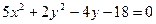тендеуимен берилген кисык турин табу

B) эллипс

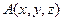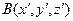жане нуктелеринин ара кашыктыгы мына формуламен табылады

D)

Уштары А(-1; 2; 4) және В(5; 2; -6) болатын кесиндини как болетин С нуктесинин координаттары

E) C(2; 2; -1)

Егер 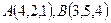болса, 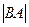-ны табу

E)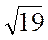

Еки нуктенін ара кашыктыгы мына формуламен аныкталады

A)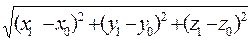

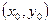Бурыштык коэффициенти жане нуктеси аркылы отетин тузудин тендеуи

B)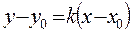

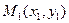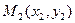жане нуктелери аркылы отетин тузудин тендеуи

D)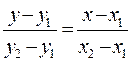

жане тузулеринин перпендикулярлык белгиси

C)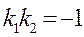

Егер Д=0,онда Ах+Ву+Сz+Д=0 жазыктыгы