Параллель проекцияның анықтамасы және қасиеттері
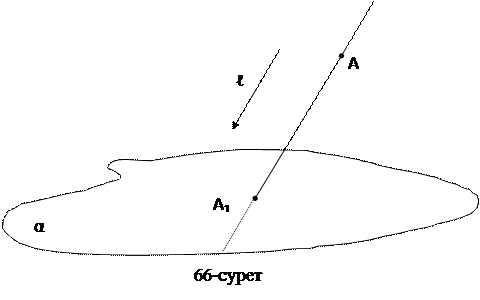 Кеңістікте α жазықтығы және одан тысқары жатқан А нүктесі берілген. α жазықтығына параллель емес қандай да бір ℓ бағытын таңдап аламыз және оны проекциялау бағыты деп атаймыз. Берілген А нүктесі арқылы ℓ бағытымен (векторымен) бағыттас түзу жүргіземіз, осы түзудің α жазықтығымен қиылысу нүктесін А
Кеңістікте α жазықтығы және одан тысқары жатқан А нүктесі берілген. α жазықтығына параллель емес қандай да бір ℓ бағытын таңдап аламыз және оны проекциялау бағыты деп атаймыз. Берілген А нүктесі арқылы ℓ бағытымен (векторымен) бағыттас түзу жүргіземіз, осы түзудің α жазықтығымен қиылысу нүктесін А  арқылы белгілейік (66-сурет). А
арқылы белгілейік (66-сурет). А  нүктесі А нүктесінің α жазықтығындағы проекциясы деп аталады. Сондай-ақ α жазықтығы - проекция жазықтығы; АА
нүктесі А нүктесінің α жазықтығындағы проекциясы деп аталады. Сондай-ақ α жазықтығы - проекция жазықтығы; АА  түзуі – проекциялаушы түзу деп аталады.
түзуі – проекциялаушы түзу деп аталады.
Параллель проекциялаудың анықтамасынан нүктенің проекциясы нүкте болатындығын көреміз.
Кеңістіктегі қандай да бір сызықтың параллель проекциясы деп проекция жазықтығындағы осы сызықтың барлық нүктелерінің проекцияларының геометриялық орнын айтады.
1-теорема: Түзудің проекциясы түзу болады.
Дәлелдеу: А  және В
және В  нүктелері АВ түзуінің сәйкесінше А және В нүктелерінің проекциясы болсын (67-сурет).
нүктелері АВ түзуінің сәйкесінше А және В нүктелерінің проекциясы болсын (67-сурет).
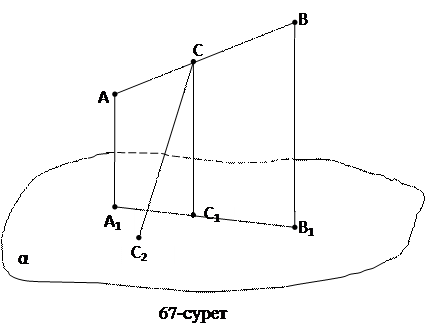 |
АВ түзуінде жататын С нүктесінің проекциясы - С  нүктесі А
нүктесі А  В
В  түзуіне тиісті емес болсын. Онда АА
түзуіне тиісті емес болсын. Онда АА  түзуіне параллель СС
түзуіне параллель СС  проекциялаушы түзуі А
проекциялаушы түзуі А  АВВ
АВВ  жазықтығынан тысқары жатады. Ал А
жазықтығынан тысқары жатады. Ал А  АВВ
АВВ  жазықтығында С нүктесі арқылы АА
жазықтығында С нүктесі арқылы АА  түзуіне параллель СС
түзуіне параллель СС  түзуін жүргізуге болады. Олай болса, С нүктесі арқылы АА
түзуін жүргізуге болады. Олай болса, С нүктесі арқылы АА  түзуіне параллель екі СС
түзуіне параллель екі СС  және СС
және СС 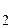 түзулері жүргізілді, ал бұл параллельдік аксиомасына қайшы. Демек, С нүктесінің проекциясы А
түзулері жүргізілді, ал бұл параллельдік аксиомасына қайшы. Демек, С нүктесінің проекциясы А  В
В  түзуіне тиісті болады. С нүктесі АВ түзуінен еркінше таңдалып алынғандықтан, АВ түзуінің кез келген нүктесінің проекциясы А
түзуіне тиісті болады. С нүктесі АВ түзуінен еркінше таңдалып алынғандықтан, АВ түзуінің кез келген нүктесінің проекциясы А  В
В  түзуіне тиісті болады.
түзуіне тиісті болады.
Салдар: Түзудің проекциясын салу үшін, оның екі нүктесінің проекциясын анықтау жеткілікті.
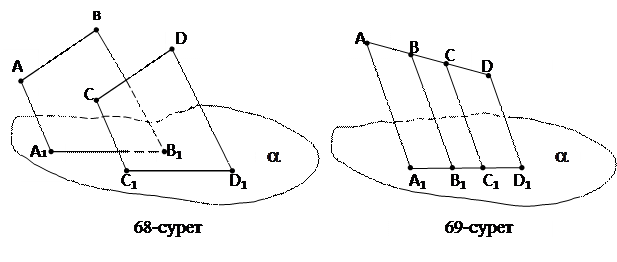
2-теорема: Параллель түзулердің проекциялары да өзара параллель болады.
Дәлелдеу: АВ және СD түзулері параллель (68-сурет). Проекциялау бағытын таңдап алып, АА  , ВВ
, ВВ  , СС
, СС  және DD
және DD  проекциялаушы түзуін жүргіземіз. АВ║СD , АА
проекциялаушы түзуін жүргіземіз. АВ║СD , АА  ║ СС
║ СС  болғандықтан сәйкесінше қиылысушы АВ, АА
болғандықтан сәйкесінше қиылысушы АВ, АА  және СD , СС
және СD , СС  түзулері арқылы өтетін А
түзулері арқылы өтетін А  АВВ
АВВ 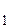 және С
және С  СDD
СDD  жазықтықтары өзара параллель. Осы параллель жазықтықтардың α проекция жазықтығымен қиылысу түзулері сәйкесінше А
жазықтықтары өзара параллель. Осы параллель жазықтықтардың α проекция жазықтығымен қиылысу түзулері сәйкесінше А  В
В 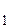 және С
және С  D
D  параллель түзулері болады. Мұндағы А
параллель түзулері болады. Мұндағы А  В
В 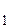 ║С
║С  D
D  түзулері сәйкесінше АВ║СD түзулерінің проекциялары.
түзулері сәйкесінше АВ║СD түзулерінің проекциялары.
3-теорема: Бір түзуде немесе параллель түзулер бойында жатқан кесінділердің ұзындықтарының қатынасы, олардың проекцияларының қатынасына тең.
Дәлелдеу: АD түзуінде жатқан АВ және СD кесінділерінің проекциялары сәйкесінше А  В
В 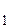 және С
және С  D
D  кесінділері болады (69-сурет).
кесінділері болады (69-сурет).
А  АDD
АDD  - проекциялаушы жазықтығын қарастырамыз. Бұл жазықтықта АD, А
- проекциялаушы жазықтығын қарастырамыз. Бұл жазықтықта АD, А  D
D  қиылысушы түзулері АА
қиылысушы түзулері АА  , ВВ
, ВВ  , СС
, СС  және DD
және DD  параллель түзулерімен қиылған.
параллель түзулерімен қиылған.
Планиметрия курсынан белгілі 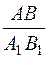 =
= 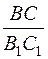 =
= 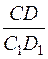 , яғни
, яғни 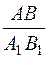 =
= 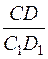 . Соңғы қатынастан дәлелдеу қажетті
. Соңғы қатынастан дәлелдеу қажетті 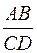 =
= 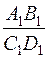 теңдігін аламыз.
теңдігін аламыз.
Егер АВ және СD кесінділері параллель түзулерде жатса, онда 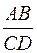 =
= 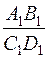 қатынасының орындалатындығын осыған ұқсас оңай дәлелдеуге болады.
қатынасының орындалатындығын осыған ұқсас оңай дәлелдеуге болады.
 |
Осы жасалған тұжырымдардан параллель проекциялаудың мынадай қасиеттері алынады:
1. Қандай да бір сызыққа тиісті нүктенің проекциясы осы сызықтың проекциясына тиісті болады.
2. Түзудің проекциясы түзу болады.
3. Параллель түзулердің проекциялары да параллель болады.
4. Проекциялауда бір түзудің немесе параллель түзулердің бойында жатқан кесінділердің қатынасы сақталады.
Бұл тұжырымдалған қасиеттер берілген түпнұсқаның проекциясын алу үшін, оның әрбір нүктесін тікелей проекциялау қажеттілігінен құтқарады. Жоғарыда анықталғандай түзудің проекциясын алу үшін, оның екі нүктесінің проекциясын анықтау жеткілікті болса, жазық фигураның проекциясын алу үшін түпнұсқаның бір түзудің бойында жатпайтын үш нүктесін тікелей проекциялау жеткілікті болады. Бұл үш нүкте базистік нүктелер деп аталады. Ал осы үш нүкте арқылы анықталатын үшбұрыш базистік үшбұрыш деп аталады.
Олай болса фигураның (жазық немесе кеңістіктік) проекциясын алу үшін, оның базистік нүктелерінің проекциясы анықталғаннан кейін, басқа нүктелерінің проекциясы тұжырымдалған 1  -4
-4  қасиеттер арқылы осы проекция жазықтығында салынады.
қасиеттер арқылы осы проекция жазықтығында салынады.
