Определение Матрицы. Виды матрицы

Матрица – это таблица из m строк и n столбцов. Произведение m×n называют размером матрицы. Обычно матрицы обозначаются большими буквами латинского алфавита: A, B, C и так далее. Элементы матриц обычно обозначаются маленькими буквами. Две матрицы одинакового размера Am×n=(aij) и Bm×n=(bij) называются равными, если их соответствующие элементы равны. Если для матрицы Am×n верно условие m≠n (т.е. количество строк не равно количеству столбцов), то часто говорят, что A – прямоугольная матрица. Если для матрицы Am×n верно условие m=n (т.е. количество строк равно количеству столбцов), то говорят, что A – квадратная матрица.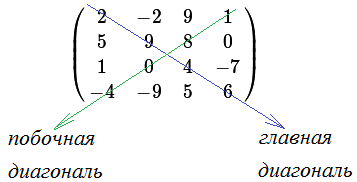

ВИДЫ

1. Прямоугольные: m и n - произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1.

5. Диагональная матрица: m=n и a_ij=0, если i≠j.

Треугольная матрица: все элементы ниже главной диагонали равны 0.

Симметрическая матрица: m=n и a_ij=a_ji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A'=A

Если все элементы матрицы Am×n равны нулю, то такая матрица называется нулевой и обозначается обычно буквой O. единичная матрица –матрица где по главной диагонали только1 .

2.Свойства операций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A')'=A

(λA)'=λ(A)'

(A+B)'=A'+B'

(AB)'=B'A'

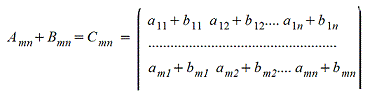
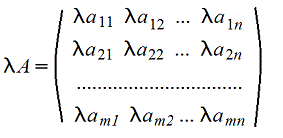
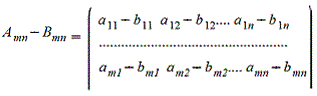
Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A'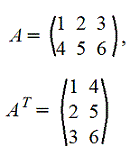

Операция сложения двух матриц.

Операция сложения определена ТОЛЬКО ДЛЯ МАТРИЦ ОДНОГО ПОРЯДКА. Другими словами, нельзя найти сумму матриц разной размерности и вообще нельзя говорить о сложении матриц разной размерности. Также нельзя говорить о сумме матрицы и числа или о сумме матрицы и какого-нибудь другого элемента.

Сложение матриц происходит почленно А=(1 2 3) В =( 2 3 4) С=А+В= (1+2 2+3 3+4 )

С= (3 5 7)

Операция умножения матрицы на число.

Операция умножения матрицы на число определена ДЛЯ МАТРИЦ ЛЮБОГО ПОРЯДКА.

матрица, элементы которой получаются умножением соответствующих элементов исходной матрицы на определенное число , умножают почленно

А=(1 2 3 4) *4 В= (1*4 2*4 3*4 4*4) В=(4 8 12 16)

Свойства операции умножения матриц.

Если матрицы А, В и С подходящих порядков, то справедливы следующие свойства операции умножения матриц.

1. Свойство ассоциативности умножения матриц .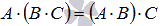

2. Два свойства дистрибутивности 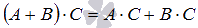и .

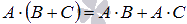3. В общем случае операция умножения матриц некоммутативна .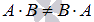

4. Единичная матрица Е порядка n на n является нейтральным элементом по умножению, то есть, для произвольной матрицы А порядка p на n справедливо равенство 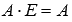, а для произвольной матрицы А порядка n на p - равенство .

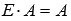Следует отметить, что при подходящих порядках произведение нулевой матрицы О на матрицуА дает нулевую матрицу. Произведение А на О также дает нулевую матрицу, если порядки позволяют проводить операцию умножения матриц.

Среди квадратных матриц существуют так называемые перестановочные матрицы, операция умножения для них коммутативна, то есть 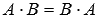. Примером перестановочных матриц является пара единичной матрицы и любой другой матрицы того же порядка, так как справедливо .

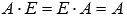Обращение матрицы

ОБРАЩЕНИЕ МАТРИЦЫ [matrix inversion] — операция получения матрицы А^–1, обратной к заданной матрице А Обращение матриц обладает следующими основными свойствами:

1.

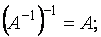
2.

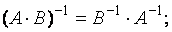
3.

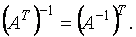
Обращение матриц часто применяется при решении так называемых матричных уравнений. Рассмотрим линейное матричное уравнение вида

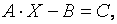
где 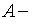заданная квадратная матрица порядка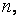 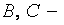заданные матрицы размерности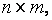 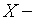неизвестная матрица размерности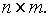

Перенесём матрицу 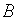в правую часть матричного уравнения:

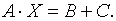
Если матрица 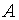невырожденная, то, по теореме 3.1, существует обратная матрица Умножая полученное выше матричное уравнение на матрицу слева (порядок умножения матриц имеет значение, потому, как следует из утверждения «3» теоремы 1.1, произведение матриц некоммутативно), получим выражение

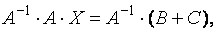или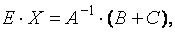

или

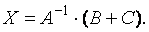
Выполняя действия в правой части последнего матричного уравнения, найдём неизвестную матрицу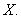

Пример. Решить матричное уравнение Матрица невырожденная, поскольку её определитель 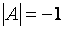отличен от ноля. Матрицу найдём любым из известных способов: 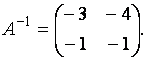Искомая матрица 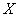может быть найдена по формуле:

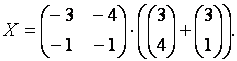
Выполняя указанные действия, получим решение матричного уравнения:

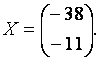
Определи́тель — одно из основных понятий линейной алгебры.
Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов.
То есть, определитель характеризует содержание матрицы. В частности, если в матрице есть линейно-зависимые строки или столбцы, — определитель равен нулю

СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть

.

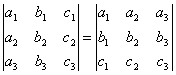СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. Например,

.

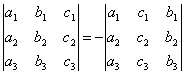СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k. Например,

.

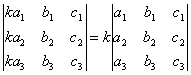СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).

СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.

СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,

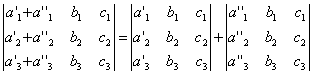
СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,

.

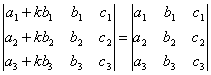Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.

Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.

Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, кторой обозначен сам элемент.

СВОЙСТВО 9. Определитель

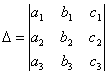
равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.