Полное приращение функции
Рассмотрим функцию двух переменных u=f(х,у).
Выберем приращения Dx и Dy – любые, но такие, что точки (x0+Dx,y0+Dy)ÎЕ(Е – некоторая окрестность точки М0(х0,у0)).
Тогда и точки (x0,y0+Dy) и (x0+Dx,y0)ÎЕ.
Разность Df=f(x0+Dx,y0+Dy)-f(x0,y0) называется полным приращением функции u=f(х,у) в точке М0(х0,у0).
В случае функции одной переменой у=f(x) в предположении существования в точке х0 конечной производной f¢(х0), для приращения функции имеет место формула:
Dу=Df(х0)=f¢(х0)×Dх+a×Dх, где a=a(Dх) и a®0 при Dх®0
Установим аналогичную формулу для функции u=f(х,у).
Теорема. Если функция u=f(х,у) и ее частные производные f¢х(х,у) и f¢у(х,у) существуют и непрерывны в точке М0(х0,у0) и некоторой ее окрестности, то справедлива формула:
Du=Df(x0,y0)=f¢х(х0,у0)×Dx+f¢у(х0,у0)×Dy+a×Dx+b×Dy (1)
где a=a(Dx), b=b(Dy) и a®0 Dx®0, b®0 Dy®0.
Доказательство. Представим полное приращение функции u=f(х,у) в виде
Df=(f(x0+Dx,y0+Dy)-f(x0,y0+Dy))+(f(x0,y0+Dy)-f(x0,y0)) (2)
Разность f(x0,y0+Dy)-f(x0,y0) представляет собой приращение функции f(x0,y) при изменении у от у0 до y0+Dy, т.е. частное приращение функции u=f(х,у) в точке М0(х0,у0). Функция f(x0,y) – функция одного аргумента у, определенная в промежутке [y0,y0+Dy].
Т.к. по условию теоремы частная производная f¢у(х,у) существует в некоторой окрестности точки М0(х0,у0), то функция f(x0,y) в промежутке [y0,y0+Dy] удовлетворяет условиям теоремы Лагранжа о конечных приращениях ( 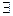 с
с 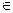 (a;b): что f(b)-f(a)=
(a;b): что f(b)-f(a)= 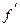 (c)(b-a))
(c)(b-a))
Следовательно,
f(x0,y0+Dy)-f(x0,y0)=f¢у(х0,у0+q1Dу)×Dу (0<q1<1) (3)
А разность f(x0+Dx,y0+Dy)-f(x0,y0+Dy) представляет собой приращение функции f(x,y0+Dy) при изменении х от х0 до х0+Dх, т.е. частное приращение функции u=f(х,у) в точке М0(х0,у0). Функция f(x,y0+Dy) – функция одного аргумента х, определенная в промежутке [х0,х0+Dх].
Т.к. по условию теоремы частная производная f¢х(х,у) существует в некоторой окрестности точки М0(х0,у0), то в этой окрестности существует и частная производная f¢х(x,y0+Dу). Следовательно, функция f(x,y0+Dу) в промежутке [х0,х0+Dх] удовлетворяет условиям теоремы Лагранжа о конечных приращениях. Т.е.
f(x0+Dx,y0+Dy)-f(x0,y0+Dy)=f¢х(х0+q2Dх,у0+Dу)×Dх (0<q2<1) (4)
Принимая во внимания соотношения (3) и (4), выражение для полного приращения Df функции u=f(х,у) в точке (x0,y0) может быть записано в виде:
Du=Df(x0,y0)=f¢х(х0+q2Dх,у0+Dу)×Dх+f¢у(х0,у0+q1Dу)×Dу (5)
По условию f¢х(х,у) и f¢у(х,у) непрерывны в точке М0(х0,у0), поэтому
f¢х(х0+q2Dх,у0+Dу)×Dх®f¢х(х0,у0) при Dх®0
f¢у(х0,у0+q1Dу)×Dу®f¢у(х0,у0) при Dу®0
Тогда можно записать:
f¢х(х0+q2Dх,у0+Dу)=f¢х(х0,у0)+a,
f¢у(х0,у0+q1Dу)=f¢у(х0,у0)+b,
где a=a(Dx), b=b(Dy) и a®0 Dx®0, b®0 Dy®0.
Тогда вместо (5) имеем:
Du=Df(x0,y0)=f¢х(х0,у0)×Dx+f¢у(х0,у0)×Dy+a×Dx+b×Dy (1) ч.т.д.
Чтобы записать формулу (1) компактней, введем в рассмотрение выражение r= 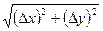 - расстояние между точками (x0,y0) и (x0+Dx,y0+Dy).
- расстояние между точками (x0,y0) и (x0+Dx,y0+Dy).
Тогда a×Dx+b×Dy= 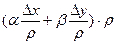 . Обозначив
. Обозначив 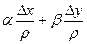 =e×r,
=e×r,
где e зависит от Dх и Dу и e®0 при r®0. Формулу (1) можно переписать в виде:
Du=f¢х(х0,у0)×Dx+f¢у(х0,у0)×Dy+e×r (6)
где e®0 при r®0.
Доказанная формула (1) распространяется и на случай функции от любого числа переменных., а именно
Пусть функция u=f(x1,…,xn) определена в некоторой открытой области Е, содержащей точку М0( 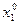 ,…,
,…, 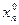 ).
).
Пусть функция f(x1,…,xn) имеет конечные частные производные  ,…,
,…, 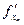 в каждой точке (x1,…,xn)ÎЕ.
в каждой точке (x1,…,xn)ÎЕ.
Пусть  ,…,
,…, 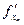 непрерывны в точке М0(
непрерывны в точке М0( 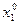 ,…,
,…, 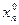 ).
).
Тогда полное приращение Df функции f(x1,…,xn) в точке М0 представимо в виде:
Df=  (
( 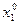 ,…,
,…, 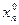 )×Dх1+
)×Dх1+ 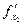 (
( 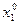 ,…,
,…, 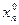 )×Dх2+…+
)×Dх2+…+ 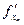 (
( 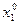 ,…,
,…, 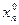 )×Dхn+a1Dx1+a2Dx2+…+anDxn
)×Dхn+a1Dx1+a2Dx2+…+anDxn
Где a1,a2,…,an®0 при r®0, где r= 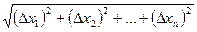
Определение. Функция u=f(x,y) называется дифференцируемой в точке М0(х0,у0), если f(x,y) определена в окрестности этой точки и полное приращение функции в точке (х0,у0) представимо в виде
Df=А×Dx+В×Dy+a×Dx+b×Dy (7)
Где А и В – постоянные числа, а a®0 и b®0 при r®0.
Теорема 1. Если функция u=f(х,у) и ее (конечные) частные производные f¢х(х,у) и f¢у(х,у) существуют и непрерывны в точке М0(х0,у0) и некоторой ее окрестности, то она дифференцируема в этой точке.
Теорема 2. Если функция u=f(х,у) дифференцируема в М0(х0,у0), то она непрерывна в этой точке (т.е. бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции)
Теорема 3. Если функция u=f(х,у) дифференцируема в М0(х0,у0), то у нее в этой точке существуют конечные частные производные f¢х и f¢у, причем f¢х(х0,у0)=А, f¢у(х0,у0)=В.
Доказательство. Из того, что функция u=f(х,у) дифференцируема в М0(х0,у0), следует, что Df=А×Dx+В×Dy+a×Dx+b×Dy, где a®0 и b®0 при r®0.
Положим Dу=0, тогда Df=Dхf=А×Dx+a×Dx Þ 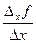 =A+aÞ
=A+aÞ 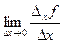 =A.
=A.
Последнее означает, что f¢х(х0,у0) существует и f¢х(х0,у0)=А.
Аналогично устанавливается, что f¢у(х0,у0) существует и f¢у(х0,у0)=В. Ч.т.д.
Теорема 4. Если у функции u=f(х,у) в точке М0(х0,у0) существуют конечные f¢х(х0,у0) и f¢у(х0,у0), то из этого не следует дифференцируемость этой функции в точке М0(х0,у0). Более того, из существования конечных f¢х(х0,у0) и f¢у(х0,у0) не следует даже непрерывность функции в точке М0(х0,у0).
Пример. f(х,у)= 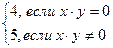
У этой функции существуют конечные f¢х(0,0)=0 и f¢у(0,0)=0, но эта функция в точке О(0,0) не является непрерывной в этой точке.
Понятие дифференцируемости функции 3-х и более переменных вводится аналогично:
Функция f(x1,…,xn) называется дифференцируемой в точке М0( 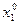 ,…,
,…, 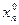 ), если ее приращение Df, вычисленное для этой точки, представимо в виде:
), если ее приращение Df, вычисленное для этой точки, представимо в виде:
Df=А1×Dх1+А2×Dх2+…+An×Dхn+a1Dx1+a2Dx2+…+anDxn, где А1,А2,…,An – некоторые постоянные числа, a1,a2,…,an®0 при r®0, где r= 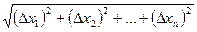
Производные сложных функций.
Теорема 1. Пусть функция u=f(х,у) определена в некоторой открытой области Е и имеет там непрерывные частные производные u¢x=f¢x(x,y) и u¢у=f¢у(x,y). Пусть функции х=j(t) и y=y(t) определены в промежутке (a,b) и имеют там конечные производные x¢t=j¢(t), y¢t=y¢(t). Пусть функции j(t) и y(t) такие, что " tÎ(a,b) точка (j(t),y(t))ÎЕ. Тогда имеет смысл сложная функция u=f(j(t),y(t))=F(t), tÎ(a,b) и " tÎ(a,b) существует конечная производная u¢t, причем
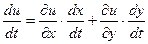 (8)
(8)
(здесь t – независимая переменная, а х,у – промежуточные аргументы.)
Доказательство. Зафиксируем любое t0Î(a,b). Пусть j(t0)=х0 и y(t0)=у0 (точка (х0,у0)ÎЕ), f(х0,у0)=u0. Дадим t0 приращение Dt¹0 и t0+DtÎ(a,b).
Пусть j(t0+Dt)=х0+Dх, y(t0+Dt)=у0+Dу, f(x0+Dx,y0+Dy)=u0+Du.
Здесь Du=f(x0+Dx,y0+Dy)-f(x0,y0) – полное приращение функции u=f(х,у) в точке (х0,у0). Для Du справедлива формула (1)
Du=f¢х(х0,у0)×Dx+f¢у(х0,у0)×Dy+a×Dx+b×Dy, где a,b®0 при r®0.
Тогда 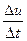 =f¢х(х0,у0)×
=f¢х(х0,у0)× 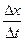 +f¢у(х0,у0)×
+f¢у(х0,у0)× 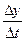 +a×
+a× 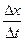 +b×
+b× 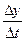 (9)
(9)
По условию, функции j(t) и y(t) имеют в (a,b) конечные производные j¢(t), y¢(t). Следовательно они непрерывны в (a,b), в частности непрерывны в t0. Но тогда Dх®0 и Dу®0 при Dt®0 Û r®0, если Dt®0 . Переходя в (9) к пределу при Dt®0, получим
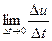 =f¢х(х0,у0)×
=f¢х(х0,у0)× 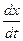 +f¢у(х0,у0)×
+f¢у(х0,у0)× 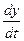
Следовательно, в точке t0 существует конечная производная 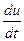 , причем
, причем
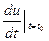 =f¢х(х0,у0)×
=f¢х(х0,у0)× 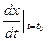 +f¢у(х0,у0)×
+f¢у(х0,у0)× 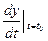
Т.к. точка t0 была выбрана произвольно, то ч.т.д.
Доказанная формула (8) распространяется и на случай функции от любого числа переменных. Т.е. когда независимая переменная одна, а промежуточных аргументов n:
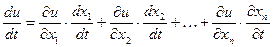 (10)
(10)
Теорема 2. Пусть функция u=f(x1,…,xn) определена в некоторой открытой области ЕÌRn и имеет там непрерывные частные производные 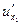 =
=  ,
, 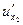 =
= 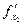 ,…,
,…, 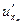 =
= 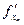 . Пусть функции x1=j1(t1,t2,…,tm), x2=j2(t1,t2,…,tm),…,xn=jn(t1,t2,…,tm) определены в области Е*ÌRm и имеют там частные производные:
. Пусть функции x1=j1(t1,t2,…,tm), x2=j2(t1,t2,…,tm),…,xn=jn(t1,t2,…,tm) определены в области Е*ÌRm и имеют там частные производные:
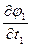 ,
, 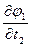 ,…,
,…, 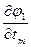 ;
; 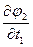 ,
, 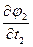 ,…,
,…, 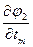 ;…;
;…; 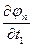 ,
, 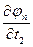 ,…,
,…, 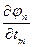 ;
;
Пусть функции j1(t1,t2,…,tm), j2(t1,t2,…,tm),…,jn(t1,t2,…,tm) такие, что "(t1,t2,…,tm)ÎЕ*Þ, что точка (j1(t1,t2,…,tm), j2(t1,t2,…,tm),…,jn(t1,t2,…,tm))ÎЕ.
Тогда имеет смысл сложная функция
u=f(j1(t1,t2,…,tm), j2(t1,t2,…,tm),…,jn(t1,t2,…,tm))=F(t1,t2,…,tm) в Е*.
и "(t1,t2,…,tm)ÎЕ* существуют частные производные 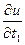 ,
, 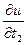 ,…,
,…, 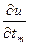 , причем
, причем
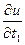 =
= 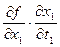 +
+ 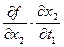 +…+
+…+ 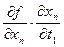 ,
,
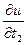 =
= 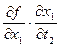 +
+ 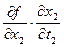 +…+
+…+ 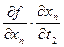 ,
,
……………………………………………………………
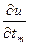 =
= 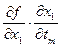 +
+ 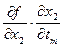 +…+
+…+ 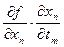 .
.
Доказательство. Чтобы вычислить 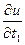 нужно в каждой из функций j1(t1,t2,…,tm), j2(t1,t2,…,tm),…,jn(t1,t2,…,tm) зафиксировать переменные t2,…,tm. Но зафиксировав t2,…,tm, мы будем в условиях теоремы 1 (или ее обобщения), т.е. получим сложную функцию одной независимой переменной t1. Следовательно, существует конечная
нужно в каждой из функций j1(t1,t2,…,tm), j2(t1,t2,…,tm),…,jn(t1,t2,…,tm) зафиксировать переменные t2,…,tm. Но зафиксировав t2,…,tm, мы будем в условиях теоремы 1 (или ее обобщения), т.е. получим сложную функцию одной независимой переменной t1. Следовательно, существует конечная 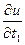 , причем
, причем 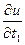 =
= 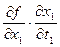 +
+ 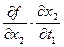 +…+
+…+ 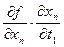 .
.
(мы воспользовались формулой (10), только вместо 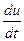 следует писать
следует писать 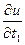 , а вместо
, а вместо 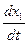 ,
, 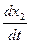 ,…,
,…, 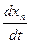 соответственно
соответственно 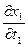 ,
, 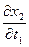 ,…,
,…, 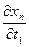 .
.
Чтобы вычислить 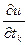 (k=2,3,…,m) нужно в каждой из функций j1(t1,t2,…,tm), j2(t1,t2,…,tm),…,jn(t1,t2,…,tm) зафиксировать все переменные, кроме tk, а затем дифференцировать полученную сложную функцию одной переменной tk. Тогда по теореме 1 (или ее обобщению), заключаем, что существует конечная
(k=2,3,…,m) нужно в каждой из функций j1(t1,t2,…,tm), j2(t1,t2,…,tm),…,jn(t1,t2,…,tm) зафиксировать все переменные, кроме tk, а затем дифференцировать полученную сложную функцию одной переменной tk. Тогда по теореме 1 (или ее обобщению), заключаем, что существует конечная 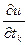 , причем
, причем
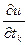 =
= 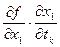 +
+ 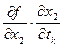 +…+
+…+ 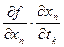 (k=2,3,…,m) ч.т.д.
(k=2,3,…,m) ч.т.д.
Полный дифференциал функции.
Пусть функция u=f(х,у) определена в некоторой открытой области Е, содержащей точку (х0,у0). Пусть функция u=f(х,у) дифференцируема в этой точке. Возьмем Dx и Dy-любые, но такие, чтобы точка (x0+Dx,y0+Dy)ÎЕ. Выражение
f¢х(х0,у0)×Dx+f¢у(х0,у0)×Dy (10)
называется полным дифференциалом функции u=f(х,у) в точке (х0,у0) и обозначается df(х0,у0) или du(х0,у0).
По определению df(х0,у0)=f¢х(х0,у0)×Dx+f¢у(х0,у0)×Dy (11)
df(х0,у0) зависит от 4-х не связанных между собой величин х0, у0,×Dx,×Dy.
Т.к. Dx=dx,×Dy=dy, то (11) можно переписать:
df(х0,у0)=f¢х(х0,у0)×dx+f¢у(х0,у0)×dy
или du= 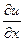 dx+
dx+ 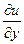 f¢ydy (12)
f¢ydy (12)
Т.о. полный дифференциал равен сумме частных дифференциалов, т.е. du=dxu+dyu.
Тогда формулу для полного приращения функции
Du=f¢х(х0,у0)×Dx+f¢у(х0,у0)×Dy+a×Dx+b×Dy, где a,b®0 при r®0 можно записать так
Du=df(х0,у0)+a×Dx+b×Dy (13), где a,b®0 при r®0
(a×Dx+b×Dy)=о(r) при r®0. Тогда из (13) следует, что полный дифференциал функции u=f(х,у) в точке (х0,у0) при r®0 отличается от полного приращения функции в этой точке на величину бесконечно малую более высокого порядка, чем r= 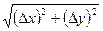 .
.
Этим пользуют при приближенных вычислениях.
Инвариантность формы полного дифференциала.
Пусть функция u=f(х,у) определена в некоторой открытой области Еху и имеет там непрерывные частные производные u¢x=f¢x(x,y) и u¢у=f¢у(x,y). Пусть функции х=j(t,h) и y=y(t,h) определены в области Еth и имеют там конечные производные x¢t, x¢h, y¢t, y¢h. Пусть функции j(t,h) и y(t,h) такие, что "(t,h)ÎЕth точка (j(t,h),y(t,h))ÎЕxy. Тогда имеет смысл сложная функция u=f(j(t,h),y(t,h))=F(t,h). При этом функция F(t,h) дифференцируема в каждой точке (t,h)ÎЕth и
du=u¢xdx+u¢ydy (14)
Т.е. соотношение (14) справедливо как в случае, когда х и у – независимые переменные, так и в случае, когда х и у – функции новых переменных.
Доказательство. (с.71-72).
Частные производные высших порядков. Теорема о равенстве смешанных производных.
Пример.
Вычислить объем материала, нужного для изготовления цилиндрического стакана размеров: Радиус внутреннего цилиндра R, высота внутреннего цилиндра H, толщина стенок и дна стакана k.(Рисунок)
1)Точное решение. Искомый объем V равен разности объемов внешнего и внутреннего цилиндров. Т.к. радиус внешнего цилиндра равен R+k, а высота H+k, то
V=π(R+k)2(H+k)-πR2H
(формула объема цилиндра - V=πR2H)
или V=π(2RНk+R2k+Hk2+ 2Rk2+k2)
Приближенное вычисление.Обозначим через f объем внутреннего цилиндра, тогда f=πR2H.
