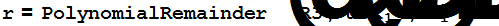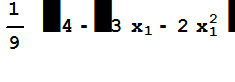Выражаем данный симметрический многочлен через основные симметрические функции

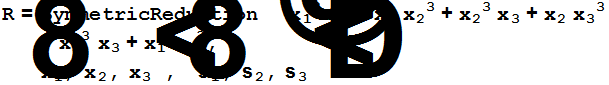
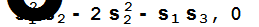
Вычисляем значения основных симметрических функций от корней данного полинома.

T={-1,-4,1};

Находим значение данного симметрического многочлена от корней данного многочлена.

R[[1]]

-35

Пример 3.6.3 Найти сумму пятых степеней корней следующего многочлена

.

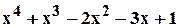Решение.

<<Algebra`SymmetricPolynomials`

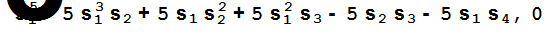
Вычисляем значения основных симметрических функций от корней данного полинома.

T={1,-2,-3,1};

Находим сумму пятых степеней корней данного полинома

R[[1]]

Пример 3.6.4. Пусть 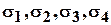основные симметрические функции от переменных 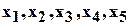, 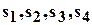основные симметрические функции от переменных 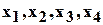. Найти зависимость между ними.

Решение.

Строим первых пять основных симметрических функций пятого порядка.

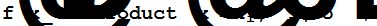
T=Table[Coefficient[f[x],x,6-n],{n,2,6}];

<<Algebra`SymmetricPolynomials`

Выражаем первые четыре основные симметрические функции пятого порядка через основные симметрические функции четвёртого порядка.

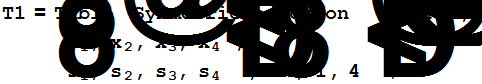
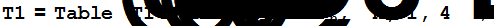
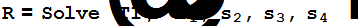
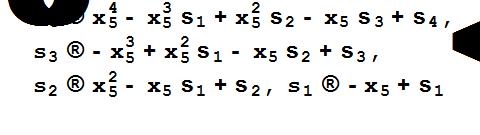
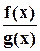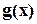Пусть - рациональная функция с рациональными коэффициентами ( и - многочлены ). Предположим далее, что 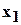- корень уравнения 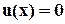, где - неприводимый над полем рациональных чисел многочлен степени . Пусть 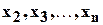- остальные корни многочлена 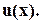Ставится задача: найти многочлен 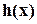степени меньше с рациональными коэффициентами и такой, что выполняется равенство

.

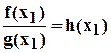Для решения поставленной задачи умножим числитель и знаменатель дроби

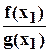
на :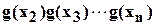

.

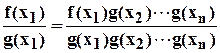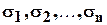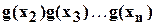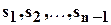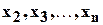Знаменатель полученной дроби будет симметрической функцией от корней многочлена . Следовательно, она выражается через основные симметрические функции от корней этого многочлена. Поэтому, в силу соотношения (3.6.2) будет рациональным числом. 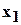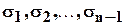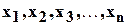В числителе произведение будет рационально выражаться через основные симметрические функции от и и, следовательно, ( мы этот факт проверили на конкретном примере, хотя он справедлив и в общем случае ) через основные симметрические функции от и 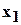. Выразив 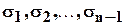через коэффициенты многочлена по формулам (3.6.2), мы получим в числителе многочлен от 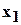с рациональными коэффициентами. Обозначим полученный многочлен через 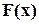. Если степень полученного многочлена не меньше , то делим его на :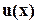

.

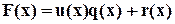Отсюда находим

).

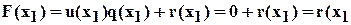Разделив 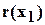на полученный ранее знаменатель, мы найдём решение рассматриваемой задачи.

Пример 3.6.5. Пусть 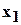- корень уравнения

.

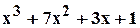Освободиться от иррациональности в знаменателе следующей дроби

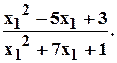
Решение.

Вводим заданные функции

f[x_]=x^2-5*x+3;

g[x_]=x^2+7*x+1;

u[x_]=x^3+7*x^2+3*x+1;

Находим значения основных симметрических функций от корней многочлена f[x]

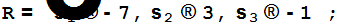
Преобразуем знаменатель данной дроби.

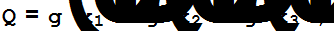
<<Algebra`SymmetricPolynomials`

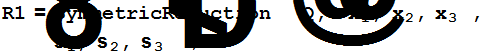
a=R1[[1]]/.R;

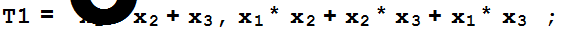
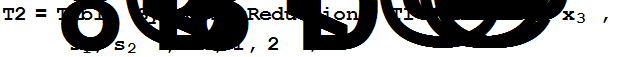
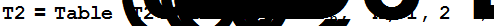
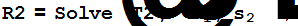
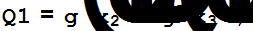
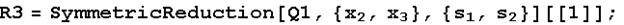
R3=Expand[R3/.R];

Находим окончательные результаты преобразований