Точечные и интервальные статистические оценки и их свойства

Точечные оценки-оценки, выраженные одним числом.

Пусть изучается дискретная генеральная совокупность относительно количественного признака х:

1. Генеральной средней называют среднее арифметическое значение признака генеральной совокупности. Если значения 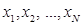различны, то

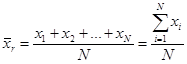=M(х)

Если значения 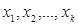имеют соответственно частоты 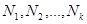, причем 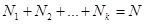, то

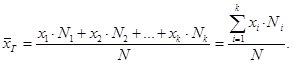=M(х)

Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема n.

Выборочным средним 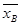называют среднее арифметическое значение признака выборочной совокупности.

Если все значения 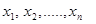признака выборки объема n различны, то:

.

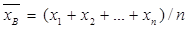Если значения признака 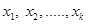имеют частоты 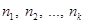соответственно, причем 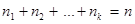, то:

.

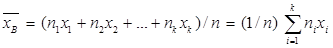Выборочная средняя применяется для оценки неизвестного математического ожидания случайной величины.

Она является несмещённой и состоятельной оценки математического ожидания.

Генеральной дисперсией Dr называется среднее арифметическое квадратов отклонения значений признака х генеральной совокупности от генеральной средней.

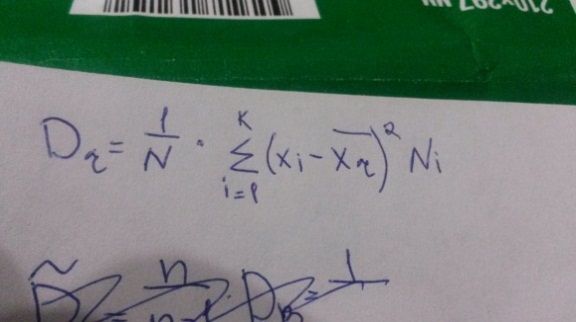
Выборочной дисперсией Dв называется среднее арифметическое квадратов отклонения наблюдаемых значений признака Х от выборочной средней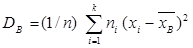

Выборочная дисперсия является состоятельной, но смещенной оценкой дисперсии.

Несмещенной и состоятельной оценкой дисперсии является исправленная выборочная дисперсия

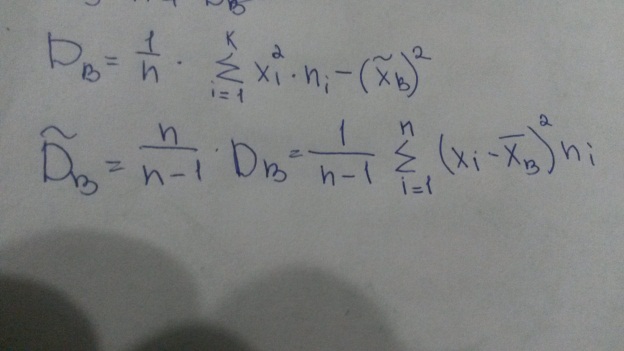
При малом объеме выборки (n<=30) пользуются исправленной выборочной дисперсией, при больших n безразлично какой пользоваться.

Для практических расчетов выборочной дисперсии используют формулу:

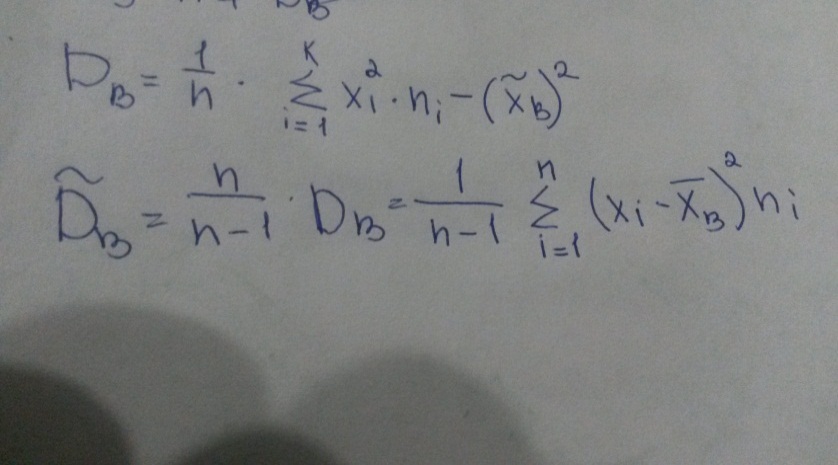
Среднее квадратичное отклонение равно корню из выборочной дисперсии

Интервальные оценки параметров распределения определяется двумя числами – концами интервала.

Интервал (Õ1; Õ2) называется доверительным для параметра О с доверительной вероятностью (надёжностью) y (0<y<1), если неравенство Õ1<O< Õ2 выполняется с вероятностью не меньше у, те

P(Õ1<O< Õ2)≥y (в символе Õ еще посередине О внутри черточка, просто не нашла такой значок)

Доверительный интервал для оценки неизвестного математического ожидания нормального распределения генеральной совокупности при известном среднем квадратическом отклонении.

вычисляется по формуле :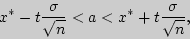

где 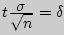- точность оценки, 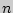- объем выборки, - выборочное среднее, 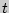- аргумент функции Лапласа, при котором 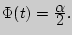где α-надежность.

Корреляция и регрессия. Метод наименьших квадратов.

Проверка статистических гипотез. Основные понятия.

Статистическая гипотеза- гипотеза либо о виде неизвестного распределения, либо о величине неизвестного параметра известного распределения.

Различают нулевую (основную) гипотезу и конкурирующую(альтернативную) гипотезу.

Существуют простые(содержат одно предположение) и сложные(содержат конечное или бесконечное число простых гипотез).

Например нулевая и простая гипотеза: х=5;

Конкурирующая: х не равно 5

Сложная: х>5

В результате проверки могут быть допущены ошибки двух родов:

1) Ошибка 1 рода - отвергнута правильная гипотеза

2) Ошибка 2 рода – принята неправильная гипотеза

Статистическим критерием называется случайная величина K, которая служит для проверки нулевой гипотезы.

Наблюдаемым значением Kнабл называют значение критерия вычисленное по выборке.

После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значение критерия, при которых нулевая гипотеза отвергается (критическая область), а другое – при которых она принимается (область принятия).

Основной принцип проверки статистических гипотез можно сформулировать так : если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если принадлежит области допустимых значений – принимают.

Критическими точками Ккр называют точки, отделяющие критическую область от области принятия гипотезы.

Правосторонней называют критическую область, определяемую неравенством: К>Ккр, Ккр>0;

Левосторонней называют критическую область, определяемую неравенством: К<Ккр, Ккр<0;

Двусторонней называют критическую область, определяемую неравенством: К<K1;K>K2, K2>K1

В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенством: |K|>Kкр

Мощность критерия называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза. Другими словами, мощность критерия есть вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза.

Пусть для проверки гипотезы принят определенный уровень значимости и выборка имеет фиксированный объём. Остается произвол в выборе критической области. Покажем, что её целесообразно построить так, чтобы мощность критерия была максимальной.

Предварительно убедимся, что если вероятность ошибки 2 рода равна β, то мощность равна 1 – β.

Действительно, если β- вероятность того, что принята нулевая гипотеза при условии, что верна конкурирующая гипотеза, то вероятность противоположного события- отвергнута нулевая гипотеза, причем справедлива конкурирующая, равна мощности критерия 1 – β..

Пусть мощность 1 – β возрастает, следовательно, уменьшается β. Таким образом, чем большемощность, тем меньше вероятность ошибки 2 рода.

Если уровень значимости уже выбран, то критическую область следует строить так, чтобы мощность критерия была максимальной.