Аналитический симплекс-метод
Аналитические методы решения задачи
Линейного программирования
Решение основной задачи линейного программирования графическим методом является наглядным в случае двух и даже трех переменных и для случаев, когда система ограничений задана в виде неравенств. Однако, такое графическое построение даже для случая трех переменных, как мы убедились, нелегко осуществимо и требует больших затрат времени, усилий воображения. Для случая же большего числа переменных графический метод становится невозможным. Для решения задач линейного программирования при большом количестве переменных удобнее пользоваться не графическими, а расчетными аналитическими методами, тем более, что для решения на вычислительных машинах эти методы более пригодны.
Для решения задач линейного программирования в общем случае разработано много методов, которые можно разделить:
1) по способу решения задачи на две группы:
Приближенные методы, которые гарантируют приближенное решение задачи. Они просты и хорошо приспособлены к обычным вычислениям (индексный метод, метод аппроксимации Фогеля и т.д.).
Конечные методы гарантируют нахождение точного решения за конечное число шагов; Конечные методы, в свою очередь, можно разделить на три группы: последовательного улучшения плана (симплекс- метод); последовательного уточнения оценок; последовательного сокращения невязок.
2) по виду решаемых задач на две группы:
универсальные, применяемые для решения широкого класса задач линейного программирования (последовательного улучшения плана; метод разрешающих множителей академика Л.В. Канторовича) и
специальные, применяемые для решения отдельных типов задач линейного программирования (распределительный закон и его модификации; метод дифференциальных рент, венгерский метод и т.д.). Они, как правило, проще универсальных, однако, приспособлены для решения узкого класса задач.
При использовании вычислительных машин универсальные методы дают возможность решать задачи линейного программирования общего вида с сотнями ограничений и практически любым числом переменных , а задачи специального вида – с тысячами ограничений (способы часто не хранятся в памяти, а воспроизводятся алгоритмически).
Среди универсальных методов нахождения оптимального решения наибольшее распространение приобрел метод последовательного улучшения допустимого решения (МПУ), имеющий много вычислительных реализаций: симплексный метод Данцига, метод обратной матрицы или модифицированный симплекс-метод, мультипликативный метод, метод разложения для задач блочной структуры, метод потенциалов для транспортной задачи и др.
Аналитический симплекс-метод.
В основе симплексного метода, наиболее разработанного и распространенного универсального методарешения основной задачи линейного программирования, лежит идея последовательного улучшения плана.
Пусть имеем систему линейных ограничений вида (3.2), заданных в виде равенств. Если ограничительные условия, либо часть ограничительных условий задана неравенствами, их необходимо привести к каноническому виду, то есть только к уравнениям путем введения, так называемых дополнительных (или балансовых, или выравнивающих) переменных.
Так как система (3.2) содержит m уравнений с n неизвестными величинами, то имеются r = n - m переменных (например, x1, x2, ..., xr), которые можно выбрать в качестве свободных, а оставшиеся m переменных (например, xr+1, xr+2, ..., xn) являются базисными переменными. Базисные переменные можно выразить через свободные переменные (по методу Джордана-Гаусса). Получим:
х r+1 = a'r+1,1 x1 + a'r+1,2 ·x2 +. . . + a'r+1,p ·xp +. . . + a'r+1,r ·xr + b'r+1
x r+2 = a'r+2,1 ·x1 + a'r+2,2 ·x2 +. . . + a'r+2,p ·xp +. . . + a'r+2,r ·xr + b'r+2
. . . . . . . (3.12)
x q = a'q,1 ·x1 + a'q,2 · x2 +. . . + a'q,p xp +. . . + a'q,r ·xr + b'q
. . . . . . .
x n = a'n,1 x1 + a'n,2 ·x2 +. . . + a'n,p ·xp +. . . + a' n,r ·xr + b'n
где b'r+1≥ 0, b'r+2 ≥ 0, . . . , b'q ≥ 0, . . . , b'n ≥ 0
Система ограничений вида (3.12) называется системой, приведенной к единичному базису (так как матрица коэффициентов при базисных переменных является единичной матрицей).
Подставляя в линейную функцию Ф вида (3.1) вместо базисных переменных их выражения через свободные из системы (3.12), получим
Ф = Гo + Г1 • x1 + Г2 • x 2 + ... + Гr • x r (3.13)
Теперь, полагая все свободные переменные равными нулю, то есть,
x1 = x2 = ... = xr = 0, найдем значения базисных переменных:
x r+1 = b'r+1, x r+2 = b'r+2, . . . , x n = b' n
Полученное таким путем решение системы (0, ..., 0, b'r+1, b'r+2, . . . , b'n) будет неотрицательным. Оно называется базисным решением (определение 3.2). Для полученного базисного решения значение целевой функции Фб = Гo. Возникает вопрос: является ли полученное опорное решение Фб = Гo минимальным?
На этот вопрос дает ответ анализ коэффициентов при свободных переменных в выражении (3.13) и в системе уравнений (3.12). При изменении значения какой-либо из свободных переменных относительно ее нулевого значения значение целевой функции Ф будет либо возрастать относительно Го (если коэффициент при свободной переменной положителен), либо убывать (если коэффициент отрицателен). При этом на величину изменения значения рассматриваемой переменной накладываются ограничения системой (3.12), исходя из условия неотрицательности переменных, входящих в систему, что определяется коэффициентами при этой переменной в данной системе.
В зависимости от значений коэффициентов при свободных переменных в системе (3.12) и в выражении целевой функции (3.13) возможны три случая:
I. Все коэффициенты при свободных переменных в выражении (3.13) неотрицательны. Тогда для любого неотрицательного решения системы (3.12) имеем значение линейной функции Ф ≥ Го. Следовательно, Го = min Ф и базисное решение системы является оптимальным, те есть задача решена.
II. Имеется свободная переменная, коэффициент при которой в выражении (3.13) отрицателен, а все коэффициенты при этой переменной в системе уравнений (3.12) - неотрицательны. То есть диапазон изменения этой переменной системой (3.12) не ограничен: она может увеличиваться до + ∞. С ростом значения этой переменной значение Ф будет неограниченно уменьшаться. В этом случае min Ф = - ∞, то есть, задача решения не имеет.
III. Имеется свободная переменная, коэффициент при которой в выражении (3.13) отрицателен, но и среди коэффициентов при этой переменной в системе уравнений (3.12) также есть отрицательные. То есть, рассматриваемая переменная может быть увеличена только до определенной величины: пока базисная переменная, в уравнение которой рассматриваемая свободная переменная входит с отрицательным коэффициентом, не станет равной нулю. (Дальнейшее увеличение свободной переменной приведет к тому, что соответствующая базисная переменная станет отрицательной, что недопустимо из условия (3.3)).
В этом случае осуществляется процедура поиска оптимального решения с применением симплексного метода. Решение задачи с помощью симплексного метода распадается на ряд шагов, заключающихся в том, что от данного базиса (б) переходим к другому базису (б') с таким расчетом, чтобы значение Ф уменьшалось или, по крайней мере, не увеличивалось, то есть, Фб' ≤ Фб. эту процедуру осуществляем до тех пор, пока не достигнем minФ.
Вычислительная процедура поиска minФ предусматривает направленный перебор угловых точек многогранника решений - области допустимых решений (ОДР) задачи линейного программирования и отыскание среди них оптимального решения за конечное число операций.
Таким образом, если задача подпадает под 3-й случай (среди коэффициентов при переменных в выражении ЦФ (3.13) есть отрицательные, но и среди коэффициентов при этой переменной в уравнениях (3.12) также есть отрицательные), выбирают другое базисное решение, то есть, в качестве свободных выбирают другой набор переменных, например, x2, x 3, . . . , x r, x r+1, а в качестве базисных– оставшиеся x1, x r+2, …, x n, которые выражают через новые свободные переменные. Получим новую систему уравнений вида (3.12).
Целевую функцию также выражают через новые свободные переменные
Ф = Г'o + Г'2 • x2 + Г'3 • x3 + ... + Г'r • xr + Г'r+1 • xr+1 (3.14)
Далее, проводят анализ коэффициентов при свободных переменных в выражении (3.14).
Если все коэффициенты при переменных в этой линейной функции положительны (случай I), то новое решение Ф = Г'о является оптимальным. Если среди коэффициентов в (3.14) есть отрицательные, то либо задача не имеет решения (случай II), либо выбирается следующий набор свободных переменных (случай III) и повторяют цикл анализа. Процедура улучшения решения продолжается до тех пор, пока не будет найдено оптимальное решение, обращающее Ф в минимум, то есть, до тех пор, пока задача не подпадет под 1-ый случай, или пока не выяснится, что оптимального решения не существует, то есть задача не подпадет под 2-ой случаи.
Итак, базисное решение задачи линейного программирования является оптимальным, если в выражении целевой функции через свободные (неосновные) переменные отсутствуют отрицательные коэффициенты при этих переменных.
Если задача линейного программирования подпадает под 3-ий случай, то переход к новому базису осуществляется следующим образом. Свободная переменная, входящая в выражение целевой функции (3.13) или (3.14) с отрицательным коэффициентом, переводится в базисные. Вместо нее в свободные переводится та базисная переменная, в уравнение которой в системе вида (3.12) рассматриваемая свободная переменная входит с отрицательным коэффициентом.
Если свободная переменная, переводимая в базисные, входит с отрицательными коэффициентами в несколько уравнений системы ограничений вида (3.12), то уравнение, базисная переменная которого раньше обращается в нуль, выбирается в качестве разрешающего, что определяется по величине градиента изменения свободной переменной, то есть по величине отношения bi/aip. Уравнение, соответствующее наименьшему значению данного градиента, то есть min(bi/aip), является разрешающим и базисная переменная, соответствующая данному уравнению, переводится в свободные.
Напомним, что мы рассматривали задачу линейного программирования, связанную с нахождением минимального значения целевой функции. В задачах, в которых требуется определить максимальное значение целевой функции, анализ сводится к определению переменных, входящих в выражения целевой функций вида (3.13) или (3.14) с положительными коэффициентами, что приводит к увеличению значения линейной функции относительно Го и Г’о. В остальном подход к решению задачи сохраняется аналогичным рассмотренному.
Таким образом, условием оптимальности в задаче на maxФ является отсутствие положительных коэффициентов при свободных переменных в выражении целевой функции, в задаче на minФ – отсутствие отрицательных коэффициентов при этих переменных.
Примечания.
1. При решении задач линейного программирования симплексным методом возникает вопрос: какие переменные выбрать в качестве базисных, какие в качестве свободных?
Существует следующее правило: любые m переменных m линейных уравнений с n переменными (m<n) называются базисными (или основными), если определитель матрицы коэффициентов при них отличен от нуля, то есть, базисный минор матрицы А отличен от нуля.
Однако, при выборе базисных переменных на первом шаге (итерации) необязательно составлять определитель из их коэффициентов и проверять, равен ли он нулю. Если система ограничительных уравнений совместна и уравнения линейно независимы, достаточно воспользоваться следующим правилом: в качестве основных (базисных) переменных на первом шаге следует выбрать (по возможности) такие m переменных, каждая из которых входит только в одно из m уравнений системы ограничений, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных.
2. Первоначальное базисное решение может оказаться недопустимым, в этом случае, не проводя проверку оптимальности решения, переводим в базисные переменные одну из тех свободных переменных с положительным коэффициентом, которые находятся в уравнении с отрицательным свободным членом (разрешающее уравнение для данного случая).
Если в этом уравнении несколько свободных переменных с положительными коэффициентами, выбираем из них ту, которая делает неотрицательным базисную переменную в этом уравнении и при этом базисные переменные в остальных уравнениях сохраняют свои неотрицательные значения.
3. Если исходное базисное решение является допустимым, то в процессе применения симплексного метода недопустимых решений появиться не может. Если они появились, это свидетельствует о наличии ошибок.
4. Выбор свободной переменной, переводимой в базисные на последующих шагах, не подчиняется какому-то правилу. Рекомендуется выбирать ту свободную переменную, которая имеет больший по абсолютной величине коэффициент в выражении целевой функции.
Идею симплексного метода проследим на конкретном примере.
********************
Пример 3.6. Минимизировать линейную функцию Ф = x1 + x2 + x3 → min
при ограничениях 7ּx1 + 2ּx2 + 9ּx3 ≥ 1
2ּx1 + 9ּx2 ≥ 1
9ּx1 + 11ּx3 ≥ 1
******************** Р Е Ш Е Н И Е ********************
Задача дана в стандартном виде (система ограничений дана в виде неравенств). Приведем ее к каноническому виду, то есть систему ограничений представим в виде уравнений, для чего в неравенства введем фиктивные переменные z1, z2, z3. Получим систему уравнений:
7ּx1 + 2ּx2 + 9ּx3 - z1 = 1,
2ּx1 + 9ּx2 - z2 = 1, (3.6.1)
9ּx1 + 11x3 - z3 =1.
Целевая функция Ф сохранит вид: Ф = x1 + x2 + x3.
Имеем 3 уравнения с 6-ю неизвестными, 3 из них (например, x1, x2, x3) выберем в качестве базисных. Оставшиеся переменные (z1, z2, z3) - в качестве свободных. Базисные переменные выразим через свободные:
x1 = 1/20 - 99/80·z1 + 11/40·z2 + 81/80·z3
x2 = 1/10 + 11/40·z1 + 1/20·z2 + 9/40·z3 (3.6.2)
x3 = 1/20 + 81/80·z1 - 9/40·z2 - 59/80·z3
целевую функцию также выразим через свободные:
Ф = 1/5 + 1/20·z1 + 1/10·z2 + 1/2·z3 (3.6.3)
Приравняем свободные переменные нулю, z1=z2=z3=0. Получим первое базисное решение Х1 = (1/20; 1/10; 1/20; 0; 0; 0) – оно допустимое (содержит только неотрицательные компоненты). При этом Ф1 = 1/5.
В выражении (3.6.3) коэффициенты при всех свободных переменных положительны – условие оптимальности выполнено. Значит, любое увеличение z1, z2, z3 сверх нуля может привести только к увеличению функции Ф, а мы хотим, чтобы она была минимальна. Задача подпадает под первый случай. Следовательно, первое допустимое базисное решение является оптимальным.
Ответ: minФ = 1/5 при Хопт = (1/20; 1/10; 1/20; 0; 0; 0).
********************
Пример 3.7. Максимизировать линейную функцию Ф = x2 + x3 → max
при ограничениях: x1 - x2 + x3 = 1,
x2 - 2·х3 + х4 = 2.
******************** Р Е Ш Е Н И Е ********************
Задача дана в каноническом виде. Система уравнений - ограничений совместна, так как ранги матрицы системы уравнений и расширенной матрицы одинаковы и равны 2. Следовательно, две переменные можно принять в качестве свободных, две другие переменные - в качестве базисных.
Шаг 1. Примем: базисные - x1, x4, свободные - x2 и х3.
Выразим базисные переменные через свободные
x1 = 1 + x2 - x3; (3.7.1)
x4 = 2 - x2 + 2·x3;
Целевая функция уже выражена через x2 и x3, то есть, сохранит свой вид:
Ф = x2 + x3 (3.7.2)
Приравняем свободные переменные нулю (х2 = х3= 0). При этом базисные переменные будут равными х1=1, х4= 2. Получим первое базисное решение Х1=(1; 0; 0; 2), оно допустимое. При этом Ф1= 0. Обе свободные переменные в целевую функцию входят с положительными коэффициентами (задача на max). Следовательно, условие оптимальности не выполняется: увеличения Ф в выражении (3.7.2) можно достичь при увеличении, например, значения х3, (x2 при этом остается равным нулю). Свободную переменную х3 переведем в базисные. Переменная x3 входит с отрицательным коэффициентом в первое уравнение системы (3.7.1), откуда видно, что х3 можно увеличивать до 1 (из условия х1≥0). Во второе уравнение x3 входит с положительным коэффициентом, то есть 2-е уравнение не ограничивает увеличение переменной x3. Следовательно, первое уравнение является разрешающим, на базе которого осуществляем переход к новому базису: переменную x1 переведем в свободные, х3 - в базисные.
Шаг 2. Теперь выберем: базисные - x3, x4; свободные - x1 и х2.
Выразим новые базисные переменные х3, x4 через новые свободные х1, х2. Получим: x3 = 1 - x1 + x2;
x4 = 4 - 2·x1 + x2; (3.7.3)
целевая функция примет вид
Ф = х2 + 1 - х1 + х2 = 1 - x1 + 2·x2 (3.7.4)
Как видно из (3.7.4), условие оптимальности не выполнено: увеличение Ф возможно при увеличении х2. В оба уравнения системы (3.7.3) х2 входит с положительными коэффициентами, то есть увеличение переменной системой уравнений (3.7.3), не ограничено. Таким образом, х2 может принимать все большие положительные значения, то есть, х2 → + ∞, при этом Ф→ + ∞ . Следовательно, maxФ = + ∞. Задача подпадает под второй случай: функция Ф не ограничена сверху, оптимального решения не существует.
Ответ: Фmах = + ∞. Задача решения не имеет.
********************
Пример 3.8. Минимизировать линейную функцию Ф = x1 + x2 + x3 → min
при ограничениях 8·x1 + 4·x2 + x3 ≥ 1
2·x1 + 5·x2 + 7·x3 ≥ 1 4·x1 + 6·x2 + 3·x3 ≥ 1
******************** Р Е Ш Е Н И Е ********************
Задача дана в стандартном виде. Для применения симплексного метода приведем ее к каноническому виду. Чтобы избавиться от знаков неравенств, введем фиктивные переменные z1, z2, z3. Ограничительные условия запишутся в виде: 8·x1 + 4·x2 + x3 - z1 = 1
2·x1 + 5·x2 + 7·x3 - z2 = 1 (3.8.2)
4·x1 + 6·x2 + 3·x3 - z3 = 1
а целевая функция сохранит вид Ф = x1 + x2 + x3.
Ранг матрицы этой системы равен 3, число переменных равно 6, количество свободных переменных равно r = n-m = 3.
Шаг 1. Выберем в качестве свободных переменные z1, z2, z3, в качестве базисных - x1, x2, x3, которые выразим через свободные. Получим:
x1 = 10/136 + 27/136·z1 + 6/136·z2 - 23/136·z3,
x2 = 12/136 - 22/136·z1 - 20/136·z2 + 54/136·z3, (3.8.3)
x3 = 8/136 + 8/136·z1 + 32/136·z2 - 32/136·z3,
Подставив эти выражения для x1, x2, x3 в целевую функцию, получим
Ф = 30/136 + 13/136 ·z1 + 18/136 ·z2 - 1/136 ·z3 (3.8.4)
Приравняем значения свободных переменных нулю z1 = z2 = z3 = 0. Получим первое базисное решение Х1 = (10/136; 12/136; 8/136; 0; 0; 0)- оно допустимое. При этом Ф1 = 30/136.
В выражение (3.8.4) свободная переменная z3 входит с отрицательным коэффициентом, следовательно, условие оптимальности не выполнено. Переменную z3 переведем в базисные. В системе (3.8.3) есть уравнения (1-ое и 3-е), в которые переменная z3 входит с отрицательными коэффициентами, ограничивающими увеличение значения z3. Задача подпадает под третий случай. То есть, увеличение z3 надо производить осторожно, чтобы величины x1 и x3, зависящие от z3, не стали при этом отрицательными.
Определим значения градиента изменения свободной переменной z3, который вычисляется отношением значения свободного члена уравнения к величине коэффициента при данной переменной. Так, для первого уравнения значение градиента переменной z3 будет равно gr1 = 10/136:23/136 = 10/23 ≈ 0,5. Для третьего уравнения - gr3 = 8/136:32/136 = 8/32 =0,25. Третье уравнение, имеющее меньшее значение градиента, будет разрешающим. Базисную переменную x3, соответствующую этому уравнению переведем в свободные.
Шаг 2. Переменные x3 и z3 меняем местами , то есть, x3→в свободные, z3→в базисные. Теперь выберем: базисные переменные - x1, x2, z3 , свободные - z1, z2, x3. Новые базисные переменные выразим через свободные. Получим:
x1 = 1/32 + 5/32·z1 - 4/32·z2 + 23/32·x3,
x2 = 6/32 - 2/32·z1 + 8/32·z2 - 54/32·x3, (3.8.5)
z3 = 8/32 + 8/32·z1 + z2 - 136/32·x3,
Целевая функция примет вид:
Ф = 7/32 + 3/32·z1 + 4/32·z2 +1/32·x3 (3.8.6)
Приравняв нулю свободные переменные z1,z2, x3 получим второе допустимое базисное решение Х2 = (1/32; 6/32; 0; 0; 0; 8/32). При этом Ф2 = 7/32.
В выражение (3.8.6) все свободные переменные входят с положительными коэффициентами, то есть, условие оптимальности выполнено (любое увеличение величин z1, z2, x3 сверх их предполагаемых нулевых значений может только увеличить значение целевой функции Ф относительно Ф2). Задача на минимизацию Ф подпадает под первый случай. Следовательно, оптимальное решение задачи найдено; второе допустимое решение является оптимальным.
Ответ: minФ = 7/32 при Хопт = (1/32; 6/32; 0; 0; 0; 8/32).
Симплекс-таблицы
Оказывается, производя расчеты по симплексному методу, нет необходимости выписывать все вычисления столь подробно, как мы рассматривали в предыдущем разделе, производить громоздкие преобразования системы линейных уравнений. Весь процесс можно записать в виде последовательности однотипно заполняемых таблиц, содержащих коэффициенты при переменных, причем каждому шагу будет соответствовать переход к следующей таблице.
Переход от одного базиса к другому при этом сводится к пересчету коэффициентов в таблицах, что осуществляется по чисто формальным правилам, хорошо приспособленным к тому же для решения на ЭВМ.
Пусть имеем систему ограничений вида (3.2), в которой r = n - m переменных (x1, ..., xr) являются свободными, а оставшиеся m переменных (xr+1, xr+2, ..., xn) - базисными. Выразив базисные переменные через свободные, приведем систему к единичному базису, но запишем в виде, несколько отличном от системы (3.12) в том смысле, что все переменные (и свободные, и базисные) запишем в левой части, а в правой части - только свободные члены.
То есть в виде
x r+1 – a r+1,1 · x1 - a r+1,2 · x2 - . . - a r+1,p · xp - . . - a r+1,r · xr = b r+1
x r+2 – a r+2,1 · x1 - a r+2,2 · x2 - . . - a r+2,p· xp - . . - a r+2,r · xr = b r+2
. . . . . . . . . . (3.15)
x q – a q,1 · x1 - a q,2 · x2 - . . - a q,p · xp - . . - a q,r · xr = b q
. . . . . . . . . .
x n – a n,1 · x1 - a n,2 · x2 - . . - a n,p · xp - . . - a n,r · xr = b n
а целевую функцию - в виде:
Ф - Г1·x1 – Г2·x2 -... - Гp·xp - ... - Гr·xr = Гo (3.16)
(с целью упрощения записи значки «’» при коэффициентах и свободных членах уравнений в системе (3.15) упущены).
Системы (3.12) и (3.15) называются приведенными к единичному базису, имея в виду, что коэффициенты при базисных переменных составляют единичную матрицу Е.
Систему (3.15) и (3.16) можно представить в виде таблицы 3.1.
Таблица 3.1.
| Базисные перемен- ные | Свобод- ные члены | свободные переменные | Базисные переменные | ||||||||
| x1 | · · · | xp | · · · | xr | x r+1 | · · · | x q | · · · | x n | ||
| x r+1 | b r+1 | -ar+1,1 | · · · | -ar+1,p | · · · | -ar+1,r | · · · | · · · | |||
| · · · | · · · | · · · | · · · | · · · | · · · | · · · | · · · | · · · | · · · | · · · | · · · |
| x q | b q | -aq,1 | · · · | - a q,p | · · · | - a q,r | · · · | · · · | |||
| · · · | · · · | · · · | · · · | · · · | · · · | · · · | · · · | · · · | · · · | · · · | · · · |
| x n | b n | -an,1 | · · · | - a n,p | · · · | - a n,r | · · · | · · · | |||
| Ф | Гo | - Г1 | · · · | - Гp | · · · | - Гr | · · · | · · · |
Хб = (0; 0; ... ;0; b r+1; b r+2; ...; b n), при этом Фб = Го
Из таблицы 3.1 определим первое базисное решение Хб и соответствующее значение целевой функции Фб: значения базисных переменных и целевой функции «снимаются» из столбца свободных членов таблицы, а свободные переменные приравниваются нулю.
Здесь коэффициенты Гj называются оценками(индексами) соответствующих переменных xj, строка таблицы, содержащая Гj ,- индексной строкой.
В соответствии с описанным в предыдущем разделе симплекс-методом мы должны, прежде всего, выяснить имеется ли в выражении (3.13) линейной функции Ф = Гo + Г1∙x1 + ... + Гj∙xj + ... + Гr∙xr хотя бы один отрицательный коэффициент при свободных переменных x1, ..., xr. Поскольку при записи в виде (3.16) и при внесении в таблицу 3.1 эти коэффициенты поменяли знаки, то мы должны, следовательно, выяснить имеются ли в последней строке таблицы положительные числа, не считая свободного члена Го.
Если таковых нет, то базисное решение, отвечающее данному базису, то есть (0; . . .; br+1, . . .; bq; . . .; bn) согласно случаю I является оптимальным, а
minФ = Го. Задача решена.
Предположим, что в последней строке имеется (не считая Го) положительная оценка - Гp>0. Отмечаем столбец, в котором она находится, вертикальной стрелкой. Этот столбец называется разрешающим столбцом.
Далее просматриваем другие элементы этого столбца. Если среди них нет положительных чисел, это означает, что все aip ≥ 0 (i = r+1,n) и задача подпадает под случай II, следовательно, min Ф = - ∞, задача решения не имеет.
И, наконец, пусть среди чисел отмеченного столбца, кроме последнего числа Гp, имеется хотя бы один положительный элемент, например, - aip > 0; Это означает, что aip < 0, задача подпадает под случай III, то есть, должны сделать следующий шаг по поиску оптимального решения. Для этого строку таблицы, в которой находится данный положительный элемент (- aip) выберем в качестве разрешающей строки. Отметим эту строку горизонтальной стрелкой.
Если в разрешающем столбце имеется несколько положительных элементов, то для соответствующих строк таблицы составим оценочные отношения bi/aip и выберем q-ю разрешающую строку из условия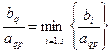 
, где s– количество строк с положительными элементами в разрешающем р-ом столбце.
Элемент таблицы, стоящий на пересечении разрешающего столбца и разрешающей строки, называется разрешающим элементом. Обведем его кружком.
С этого момента начинается перестройка таблицы, цель которой состоит в переходе к новому базису, содержащему переменную xp базисной вместо xq (из таблицы 3.1 видно, что p ≤ r; r+1≤q ≤ n), то есть, q из числа базисных переменных, p - из числа свободных.
Перестройка осуществляется при помощи метода Джордана-Гаусса, как и в аналитическом симплекс-методе. А именно, умножим выделенную разрешающую q-ю строку на такое число, чтобы на месте разрешающего элемента появилась единица, то есть, умножим на 1/aqp. Это соответствует тому, что q-ое уравнение разрешается относительно новой базисной переменной xp.
Полученную таким образом строку запишем в новую таблицу на прежнее место, то есть в виде q-ой строки, но с новой базисной переменной xp вместо xq. Затем к каждой из остальных строк таблицы 3.1 прибавляем разрешающую строку, умноженную на такое число, чтобы в клетке отмеченного столбца появился нуль - это соответствует исключению неизвестной xp из остальных уравнений, а также из выражения для Ф. Преобразованные таким образом строки пишем в новую таблицу на место прежних строк.
К новой таблице применяется та же процедура. В результате или находится оптимальное решение (случай I), или обнаруживается, что minФ = - ∞ (случай II), или же производится следующий шаг по поиску оптимального решения (случай III) – переходим к новой таблице. И так далее, пока процесс не остановится, то есть, пока не придем к случаю I или случаю II.
Рассмотренная процедура решения изложена применительно к задачам линейного программирования на отыскание минимального значения целевой функции. В задачах, в которых требуется определить максимальное значение целевой функции, анализ индексной строки сводится к выяснению наличия в этой строке отрицательных (кроме Го) оценок, что приводит к увеличению значения целевой функции относительно Фб = Го. в остальном подход к решению задачи сохраняется аналогичным рассмотренному.
Итак, при решении задач ЛП с помощью симплексных таблиц условием оптимальности в задачах на отыскание maxФ является отсутствие отрицательных оценок в индексной строке таблицы, в задачах на отыскание minФ - отсутствие положительных оценок в этой строке.
Вышеизложенное можно записать в виде следующего алгоритма.
1. Выделим исходный допустимый базис и заполним первую таблицу.
2. Если в оценочной строке полученной таблицы нет положительных чисел, кроме Го, то базисное решение является оптимальным - задача решена.
3. Пусть в оценочной строке имеется положительное число, скажем, Гp (в столбце xp). Отметим столбец xp (разрешающий столбец) вертикальной стрелкой. Просматриваем остальные числа этого столбца. Если среди них нет положительных чисел, то min Ф = -∞ - задача решения не имеет.
4. Если в разрешающем столбце имеются положительные числа, для каждого из этих чисел akp (k ≤ r) составляем оценочное отношение bk/akp, где bk - первое число в этой строке (свободный член). Из всех таких отношений выбираем наименьшее. Пусть оно соответствует строке для базисной переменной xq. Отметим эту строку (разрешающую строку) горизонтальной стрелкой. Отметим кружочком число aqp, стоящее в пересечении отмеченной строки и отмеченного столбца - разрешающий элемент таблицы.
5. Переходим к новой таблице. Для этого отмеченную строку умножаем на 1/aqp (чтобы на месте разрешающего элемента появилась единица) и запишем ее в новой таблице на месте прежней с новой базисной переменной xp. К каждой из остальных строк таблицы прибавляем отмеченную строку, умноженную на (-aip/aqp), либо строку, полученную на месте отмеченной строки, умноженную на (-aip), чтобы элемент, стоящий в отмеченном столбце, обратился в 0. Полученную строку пишем на месте прежней.
6. С новой таблицей возвращаемся к выполнению пункта 2.
Примечания.
1) на практике при решении задач ЛП удобнее все переменных в столбцах симплекс-таблицы размещать в порядке возрастания их индексов (номеров), не разделяя их на базисные и свободные, как это было сделано в таблице 3.1 для удобства теоретического изложения;
2) практически удобнее все таблицы "пристыковывать" друг к другу (через строку) по вертикали, что позволяет для остальных таблиц, начиная со второй, не писать заглавную строку, то есть, "шапку" таблицы.
3) Если на каком-либо этапе расчета возникает неопределенность в выборе разрешающей строки (оказывается несколько равных минимальных отношений bk/akp), то следует выбирать ту строку, для которой отношение элементов первого столбца свободных переменных к разрешающему столбу является наименьшим. Если при этом снова оказываются равные минимальные отношения, то составляют отношения элементов следующего столбца свободных переменных, и так до тех пор, пока разрешающая строка не определится однозначно.
***************
Пример 3.9. Найти наибольшее значение линейной функции
Ф = 7·x1 + 5·x2 → max
при ограничениях: 2·x1 + 3·x2 + x3 = 19,
2·x1 + x2 + x4 = 13,
3·x2 + x5 = 15,
3·x1 + x6 = 18.
******************** Р Е Ш Е Н И Е ********************
Задача дана в каноническом виде. Имеем систему 4 уравнений с 6 неизвестными переменными. Следовательно, m=4 переменные принять в качестве базисных, а r=n-m=2 переменные – в качестве свободных.
Шаг 1. Выберем в качестве свободных х1 и х2. Выразим базисные переменные х3, х4, х5, х6 через свободные, то есть, приведем систему уравнений к единичному базису и запишем в виде, удобном для применения симплекс-таблиц: x3 + 2·x1 + 3·x2 = 19,
x4 + 2·x1 + x2 = 13,
x5 + 3·x2 = 15,
x6 + 3·x1 = 18.
Целевая функция Ф = 7·x1 + 5·x2 уже выражена через свободные переменные, запишем ее в виде Ф - 7·x1 - 5·x2 = 0.
Заполним исходную таблицу (табл. 3.9.1).
Из этой таблицы определим первое базисное решение Х1= (0; 0; 19; 13; 15; 18) – оно допустимое, и соответствующее значение целевой функции Ф1= 0.
В индексной строке таблицы 3.9.1 имеются отрицательные оценки: -7 и –5 в столбцах х1 и х2. То есть, условие оптимальности не выполнено (при увеличении значений этих переменных значение Ф будет возрастать). Примем к рассмотрению, например, -5 в столбце х2 (переведем ее в базисные) и выделим соответствующий (разрешающий) столбец стрелкой. В этом столбце имеются три положительных элемента: 3, 1, 3 в строках х3, х4, х5.
Вычислим для этих строк оценочные отношения: разделим на эти числа соответствующие свободные члены, получим 19/3, 13/1, 15/3, из которых наименьшее - 15/3 - в строке для х5. Следовательно, строка х5 является разрешающей. Выделим ее стрелкой. Число 3, находящееся на пересечении разрешающей строке и разрешающего столбце, (обведено кружочком) является разрешающим элементом таблицы. На базе этого элемента переходим к новому базису, для чего переменные х2 и х5 меняем местами.
Шаг 2. Базисные переменные - х3, х4, х2, х6. Для составления следующей таблицы разрешающую строку таблицы 3.9.1 умножим на 1/3, чтобы получить на месте разрешающего элемента 1, и полученную таким образом строку пишем в новую таблицу 3.9.2 на месте прежней с базисной переменной х2.
К каждой из остальных строк прибавляем разрешающую, умноженную на такое число (коэффициент перехода), чтобы в соответствующих клетках столбца для х2 появились нули, и преобразованные строки запишем в новую таблицу на прежние места. Этим завершается 1 итерация.
Теперь все рассуждения повторяются применительно к табл. 3.9.2. Вторым допустимым базисным решением является Х2= (0; 5; 4; 8; 0; 18), при этом Ф2= 25. В индексной строке таблицы 3.9.2 имеется отрицательная оценка –7 в столбце х1 (разрешающий). Строка х3 с наименьшим значением оценочного отношения является разрешающей строкой, элемент 2, находящийся на пересечении столбца х1 и строки х3, есть разрешающий элемент. На базе этого элемента переходим к новому базису, то есть, к следующей таблице 3.9.3.
Шаг 3. Базисные переменные – х1, х4, х2, х6. Из таблицы 3.9.3 находим третье допустимое базисное решение Х3= (2; 5; 0; 4; 0; 12), при этом Ф3= 39. В индексной строке таблицы имеется отрицательная оценка –11/6 в столбце х5 (разрешающий столбец), в котором имеются 3 положительных элемента в строках х4, х2, х6. Строка х4 – разрешающая строка, элемент 2/3 – разрешающий элемент, на базе которого переходим к новому базису, то есть, к таблице 3.9.4.
Шаг 4. Базисные переменные – х1, х5, х2, х6. Четвертое допустимое решение Х4= (5; 3; 0; 0; 6; 3), при этом Ф4= 50. В индексной строке таблицы 3.9.4 нет отрицательных оценок, условие оптимальности выполнено, следовательно, получили оптимальное решение и наибольшее значение целевой функции.
Ответ: maxФ = 50 при Хопт= (5; 3; 0; 0; 6; 3).